1. READ THE PROBLEM.
   
   
2. READ THE PROBLEM AGAIN.  Okay, this may be a little bit of overkill here.  However, the point of these first two steps is that you must read the problem. This step is the MOST important step, but it is also the step that most people don’t do properly.
   
   You need to read the problem very carefully and as many times as it takes.  You are only done with this step when you have completely understood what the problem is asking you to do.  This includes identifying all the given information and identifying what you being asked to find.
   
   Again, it can’t be stressed enough that you’ve got to carefully read the problem.  Sometimes a single word can completely change how the problem is worked.  If you just skim the problem you may well miss that very important word.
   
   
3. Represent one of the unknown quantities with a variable and try to relate all the other unknown quantities (if there are any of course) to this variable.
   
   
4. If applicable, sketch a figure illustrating the situation.  This may seem like a silly step, but it can be incredibly helpful with the next step on occasion.
   
   
5. Form an equation that will relate known quantities to the unknown quantities.  To do this make use of known formulas and often the figure sketched in the previous step can be used to determine the equation.
   
   
6. Solve the equation formed in the previous step and write down the answer to all the questions.  It is important to answer all the questions that you were asked.  Often you will be asked for several quantities in the answer and the equation will only give one of them.
   
   
7. Check your answer.  Do this by plugging into the equation, but also use intuition to make sure that the answer makes sense.  Mistakes can often be identified by acknowledging that the answer just doesn’t make sense.

Example 1  In a certain Algebra class there is a total of 350 possible points.  These points come from 5 homework sets that are worth 10 points each and 3 hour exams that are worth 100 points each.  A student has received homework scores of 4, 8, 7, 7, and 9 and the first two exam scores are 78 and 83.  Assuming that grades are assigned according to the standard scale and there are no weights assigned to any of the grades is it possible for the student to receive an A in the class and if so what is the minimum score on the third exam that will give an A?  What about a B?

Solution

Okay, let’s start off by defining p to be the minimum required score on the third exam.

Now, let’s recall how grades are set.  Since there are no weights or anything on the grades, the grade will be set by first computing the following percentage.

Since we are using the standard scale if the grade percentage is 0.9 or higher the student will get an A.  Likewise if the grade percentage is between 0.8 and 0.9 the student will get a B.

We know that the total possible points is 350 and the student has a total points (including the third exam) of,

The smallest possible percentage for an A is 0.9 and so if  p is the minimum required score on the third exam for an A we will have the following equation.

This is a linear equation that we will need to solve for p.

So, the minimum required score on the third exam is 119.  This is a problem since the exam is worth only 100 points.  In other words, the student will not be getting an A in the Algebra class.

Now let’s check if the student will get a B.  In this case the minimum percentage is 0.8.  So, to find the minimum required score on the third exam for a B we will need to solve,

Solving this for p gives,

So, it is possible for the student to get a B in the class.  All that the student will need to do is get at least an 84 on the third exam.

Example 2  We want to build a set of shelves.  The width of the set of shelves needs to be 4 times the height of the set of shelves and the set of shelves must have three shelves in it.  If there are 72 feet of wood to use to build the set of shelves what should the dimensions of the set of shelves be?

Solution

We will first define x to be the height of the set of shelves.  This means that 4x is width of the set of shelves.  In this case we definitely need to sketch a figure so we can correctly set up the equation.  Here it is,

Now we know that there are 72 feet of wood to be used and we will assume that all of it will be used.  So, we can set up the following word equation.

It is often a good idea to first put the equation in words before actually writing down the equation as we did here.  At this point, we can see from the figure there are two vertical pieces; each one has a length of x.  Also, there are 4 horizontal pieces, each with a length of 4x. So, the equation is then,

So, it looks like the height of the set of shelves should be 4 feet.  Note however that we haven’t actually answered the question however.  The problem asked us to find the dimensions.  This means that we also need the width of the set of shelves.  The width is 4(4)=16 feet.  So the dimensions will need to be 4x16 feet.

Example 3  A calculator has been marked up 15% and is being sold for $78.50.  How much did the store pay the manufacturer of the calculator?

Solution

First, let’s define p to be the cost that the store paid for the calculator.  The stores markup on the calculator is 15%.  This means that 0.15p has been added on to the original price (p) to get the amount the calculator is being sold for.  In other words, we have the following equation

that we need to solve for p.  Doing this gives,

The store paid $68.26 for the calculator.  Note that since we are dealing with money we rounded the answer down to two decimal places.

Example 4  A shirt is on sale for $15.00 and has been marked down 35%.  How much was the shirt being sold for before the sale?

Solution

This problem is pretty much the opposite of the previous example.  Let’s start with defining p to be the price of the shirt before the sale.  It has been marked down by 35%.  This means that 0.35p has been subtracted off from the original price.  Therefore, the equation (and solution) is,

So, with rounding it looks like the shirt was originally sold for $23.08.

Example 5  Two cars are 500 miles apart and moving directly towards each other.  One car is moving at a speed of 100 mph and the other is moving at 70 mph.  Assuming that the cars start moving at the same time how long does it take for the two cars to meet?

Solution

Let’s let t represent the amount of time that the cars are traveling before they meet.  Now, we need to sketch a figure for this one.  This figure will help us to write down the equation that we’ll need to solve.

From this figure we can see that the Distance Car A travels plus the Distance Car B travels must equal the total distance separating the two cars, 500 miles.

Here is the word equation for this problem in two separate forms.

We used the standard formula here twice, once for each car.  We know that the distance a car travels is the rate of the car times the time traveled by the car.  In this case we know that Car A travels at 100 mph for t hours and that Car B travels at 70 mph for t hours as well.  Plugging these into the word equation and solving gives us,

So, they will travel for approximately 2.94 hours before meeting.

Example 6  Repeat the previous example except this time assume that the faster car will start 1 hour after slower car starts.

Solution

For this problem we are going to need to be careful with the time traveled by each car.  Let’s let t be the amount of time that the slower travel car travels.  Now, since the faster car starts out 1 hour after the slower car it will only travel for  hours.

Now, since we are repeating the problem from above the figure and word equation will remain identical and so we won’t bother repeating them here.  The only difference is what we substitute for the time traveled for the faster car.  Instead of t as we used in the previous example we will use  since it travels for one hour less that the slower car.

Here is the equation and solution for this example.

In this case the slower car will travel for 3.53 hours before meeting while the faster car will travel for 2.53 hrs (1 hour less than the slower car…).

Example 7  Two boats start out 100 miles apart and start moving to the right at the same time.  The boat on the left is moving at twice the speed as the boat on the right.  Five hours after starting the boat on the left catches up with the boat on the right.  How fast was each boat moving?

Solution

Let’s start off by letting r be the speed of the boat on the right (the slower boat).  This means that the boat to the left (the faster boat) is moving at a speed of 2r.  Here is the figure for this situation.

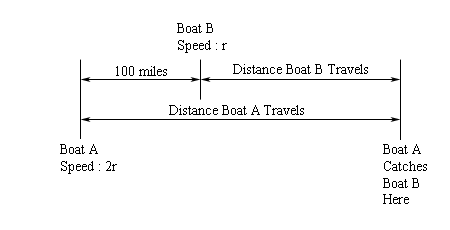
From the figure it looks like we’ve got the following word equation.

Upon plugging in the standard formula for the distance gives,

For this problem we know that the time each is 5 hours and we know that the rate of Boat A is 2r and the rate of Boat B is r.  Plugging these into the work equation and solving gives,

So, the slower boat is moving at 20 mph and the faster boat is moving at 40 mph (twice as fast).

Example 8  An office has two envelope stuffing machines.  Machine A can stuff a batch of envelopes in 5 hours, while Machine B can stuff a batch of envelopes in 3 hours.  How long would it take the two machines working together to stuff a batch of envelopes?

Solution

Let t be the time that it takes both machines, working together, to stuff a batch of envelopes.  The word equation for this problem is,

We know that the time spent working is t however we don’t know the work rate of each machine.  To get these we’ll need to use the initial information given about how long it takes each machine to do the job individually.  We can use the following equation to get these rates.

Let’s start with Machine A.

Now, Machine B.

Plugging these quantities into the main equation above gives the following equation that we need to solve.

So, it looks like it will take the two machines, working together, 1.875 hours to stuff a batch of envelopes.

Example 9  Mary can clean an office complex in 5 hours.  Working together John and Mary can clean the office complex in 3.5 hours.  How long would it take John to clean the office complex by himself?

Solution

Let t be the amount of time it would take John to clean the office complex by himself.  The basic word equation for this problem is,

This time we know that the time spent working together is 3.5 hours.  We now need to find the work rates for each person.  We’ll start with Mary.

Now we’ll find the work rate of John.  Notice however, that since we don’t know how long it will take him to do the job by himself we aren’t going to be able to get a single number for this.  That is not a problem as we’ll see in a second.

Notice that we’ve managed to get the work rate of John in terms of the time it would take him to do the job himself.  This means that once we solve the equation above we’ll have the answer that we want.  So, let’s plug into the work equation and solve for the time it would take John to do the job by himself.

So, it looks like it would take John 11.67 hours to clean the complex by himself.

Example 10  How much of a 50% alcohol solution should we mix with 10 gallons of a 35% solution to get a 40% solution?

Solution

Okay, let x be the amount of 50% solution that we need.  This means that there will be  gallons of the 40% solution once we’re done mixing the two.

Here is the basic work equation for this problem.

Now, plug in the volumes and solve for x.

So, we need 5 gallons of the 50% solution to get a 40% solution.

Example 11  We have a 40% acid solution and we want 75 liters of a 15% acid solution.  How much water should we put into the 40% solution to do this?

Solution

Let x be the amount of water we need to add to the 40% solution.  Now, we also don’t how much of the 40% solution we’ll need.  However, since we know the final volume (75 liters) we will know that we will need  liters of the 40% solution.

Here is the word equation for this problem.

Notice that in the first term we used the “Amount of acid in the water”.  This might look a little weird to you because there shouldn’t be any acid in the water.  However, this is exactly what we want.  The basic equation tells us to look at how much of the secondary liquid is in the water.  So, this is the correct wording.  When we plug in the percentages and volumes we will think of the water as a 0% percent solution since that is in fact what it is.  So, the new word equation is,

Do not get excited about the zero in the first term.  This is okay and will not be a problem.  Let’s now plug in the volumes and solve for x.

So, we need to add in 46.875 liters of water to 28.125 liters of a 40% solution to get 75 liters of a 15% solution.