You can navigate through this E-Book using the menu to the left. For E-Books that have a Chapter/Section organization each option in the menu to the left indicates a chapter and will open a menu showing the sections in that chapter. Alternatively, you can navigate to the next/previous section or chapter by clicking the links in the boxes at the very top and bottom of the material.
Also, depending upon the E-Book, it will be possible to download the complete E-Book, the chapter containing the current section and/or the current section. You can do this be clicking on the E-Book, Chapter, and/or the Section link provided below.
For those pages with mathematics on them you can, in most cases, enlarge the mathematics portion by clicking on the equation. Click the enlarged version to hide it.
The purpose of this section is to remind us of one of the
more important applications of derivatives.
That is the fact that 
represents the rate of change of . This is an application that we repeatedly saw
in the previous chapter. Almost every
section in the previous chapter contained at least one problem dealing with
this application of derivatives. While this
application will arise occasionally in this chapter we are going to focus more
on other applications in this chapter.
So, to make sure that we don’t forget about this application
here is a brief set of examples concentrating on the rate of change application
of derivatives. Note that the point of
these examples is to remind you of material covered in the previous chapter and
not to teach you how to do these kinds of problems. If you don’t recall how to do these kinds of
examples you’ll need to go back and review the previous chapter.
|
Example 1 Determine
all the points where the following function is not changing.
Solution
First we’ll need to take the derivative of the function.
Now, the
function will not be changing if the rate of change is zero and so to answer
this question we need to determine where the derivative is zero. So, let’s set this equal to zero and solve.
The solution to
this is then,
If you don’t
recall how to solve trig equations check out the Solving Trig Equations sections in the
Review Chapter.
|
|
Example 2 Determine
where the following function is increasing and decreasing.
Solution
As with the first problem we first need to take the derivative
of the function.
Next, we need
to determine where the function isn’t changing. This is at,
So, the
function is not changing at three values of t. Finally, to determine
where the function is increasing or decreasing we need to determine where the
derivative is positive or negative.
Recall that if the derivative is positive then the function must be
increasing and if the derivative is negative then the function must be
decreasing. The following number line
gives this information.
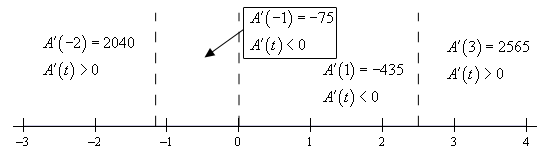
So, from this
number line we can see that we have the following increasing and decreasing
information.
|
If you don’t remember how to solve polynomial and rational
inequalities then you should check out the appropriate sections in the Review
Chapter.
Finally, we can’t forget about Related
Rates problems.
|
Example 3 Two
cars start out 500 miles apart. Car A
is to the west of Car B and starts driving to the east (i.e. towards Car B) at 35 mph and at the same time Car B starts
driving south at 50 mph. After 3 hours
of driving at what rate is the distance between the two cars changing? Is it increasing or decreasing?
Solution
The first thing to do here is to get sketch a figure
showing the situation.
In this figure y represents the distance driven by
Car B and x represents the distance
separating Car A from Car B’s initial position and z represents the distance separating the two cars. After 3 hours driving time with have the
following values of x and y.
We can use the
Pythagorean theorem to find z at
this time as follows,
Now, to answer
this question we will need to determine given that and . Do you agree with the signs on the two
given rates? Remember that a rate is
negative if the quantity is decreasing and positive if the quantity is
increasing.
We can again
use the Pythagorean theorem here.
First, write it down and the remember that x, y, and z are all changing with time and so
differentiate the equation using Implicit
Differentiation.
Finally, all we
need to do is cancel a two from everything, plug in for the known quantities
and solve for .
So, after three
hours the distance between them is decreasing at a rate of 14.9696 mph.
|
So, in this section we covered three “standard” problems
using the idea that the derivative of a function gives its rate of change. As mentioned earlier, this chapter will e
focusing more on other applications than the idea of rate of change, however,
we can’t forget this application as it is a very important one.