Example 1  A window is being built and the bottom is a rectangle and the top is a semicircle.  If there is 12 meters of framing materials what must the dimensions of the window be to let in the most light?

Solution

Okay, let’s ask this question again is slightly easier to understand terms.  We want a window in the shape described above to have a maximum area (and hence let in the most light) and have a perimeter of 12 m (because we have 12 m of framing material).  Little bit easier to understand in those terms.

Here’s a sketch of the window.  The height of the rectangular portion is h and because the semicircle is on top we can think of the width of the rectangular portion at 2r.

The perimeter (our constraint) is the lengths of the three sides on the rectangular portion plus half the circumference of a circle of radius r.  The area (what we want to maximize) is the area of the rectangle plus half the area of a circle of radius r.  Here are the equations we’ll be working with in this example.

In this case we’ll solve the constraint for h and plug that into the area equation.

The first and second derivatives are,

We can see that the only critical point is,

We can also see that the second derivative is always negative (in fact it’s a constant) and so we can see that the maximum area must occur at this point.  So, for the maximum area the semicircle on top must have a radius of 1.6803 and the rectangle must have the dimensions 3.3606 x 1.6803 (h x 2r).

Example 2  Determine the area of the largest rectangle that can be inscribed in a circle of radius 4.

Solution

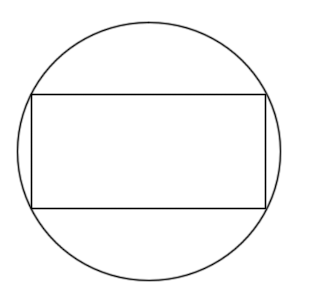
Huh?  This problem is best described with a sketch.  Here is what we’re looking for.

We want the area of the largest rectangle that we can fit inside a circle and have all of its corners touching the circle.

To do this problem it’s easiest to assume that the circle (and hence the rectangle) is centered at the origin.  Doing this we know that the equation of the circle will be

and that the right upper corner of the rectangle will have the coordinates .  This means that the width of the rectangle will be 2x and the height of the rectangle will be 2y.  The area of the rectangle will then be,

So, we’ve got the function we want to maximize (the area), but what is the constraint?  Well since the coordinates of the upper right corner must be on the circle we know that x and y must satisfy the equation of the circle.  In other words, the equation of the circle is the constraint.

The first thing to do then is to solve the constraint for one of the variables.

Since the point that we’re looking at is in the first quadrant we know that y must be positive and so we can take the “+” part of this.  Plugging this into the area and computing the first derivative gives,

Before getting the critical points let’s notice that we can limit x to the range  since we are assuming that x is in the first quadrant and must stay inside the circle.  Now the four critical points we get (two from the numerator and two from the denominator) are,

We only want critical points that are in the range of possible optimal values so that means that we have two critical points to deal with :  and .  Notice however that the second critical point is also one of the endpoints of our interval.

Now, area function is continuous and we have an interval of possible solution with finite endpoints so,

So, we can see that we’ll get the maximum area if  and the corresponding value of y is,

It looks like the maximum area will be found if the inscribed rectangle is in fact a square.

Example 3  Determine the point(s) on  that are closest to (0,2).

Solution

Here’s a quick sketch of the situation.

So, we’re looking for the shortest length of the dashed line.  Notice as well that if the shortest distance isn’t at  there will be two points on the graph, as we’ve shown above, that will give the shortest distance.  This is because the parabola is symmetric to the y-axis and the point in question is on the y-axis.  This won’t always be the case of course so don’t always expect two points in these kinds of problems.

In this case we need to minimize the distance between the point (0,2) and any point that is one the graph (x,y).  Or,

If you think about the situation here it makes sense that the point that minimizes the distance will also minimize the square of the distance and so since it will be easier to work with we will use the square of the distance and minimize that.  If you aren’t convinced of this we’ll take a closer look at this after this problem.  So, the function that we’re going to minimize is,

The constraint in this case is the function itself since the point must lie on the graph of the function.

At this point there are two methods for proceeding.  One of which will require significantly more work than the other.  Let’s take a look at both of them.

Solution 1

In this case we will use the constraint in probably the most obvious way.  We already have the constraint solved for y so let’s plug that into the square of the distance and get the derivatives.

So, it looks like there are three critical points for the square of the distance and notice that this time, unlike pretty much every previous example we’ve worked, we can’t exclude zero or negative numbers.  They are perfectly valid possible optimal values this time.

Before going any farther, let’s check these in the second derivative to see if they are all relative minimums.

So,  is a relative maximum and so can’t possibly be the minimum distance.  That means that we’ve got two critical points. The question is how do we verify that these give the minimum distance and yes we did mean to say that both will give the minimum distance.  Recall from our sketch above that if x gives the minimum distance then so will x and so if gives the minimum distance then the other should as well.

None of the methods we discussed in the previous section will really work here.  We don’t have an interval of possible solutions with finite endpoints and both the first and second derivative change sign.  In this case however, we can still verify that they are the points that give the minimum distance.

First, notice that if we are working on the interval  then the endpoints of this interval (which are also the critical points) are in fact where the absolute minimum of the function occurs in this interval. 

Next we can see that if  then .  Or in other words, if  the function is decreasing until it hits  and so must always be larger than the function at .

Similarly,   then  and so the function is always increasing to the right of   and so must be larger than the function at .

So, putting all of this together tells us that we do in fact have an absolute minimum at .

All that we need to do is to find the value of y for these points.

So, the points on the graph that are closest to (0,2) are,

Solution 2

The first solution that we worked was actually the long solution.  There is a much shorter solution to this problem.  Instead of plugging y into the square of the distance let’s plug in x.  From the constraint we get,

and notice that the only place x show up in the square of the distance it shows up as x² and let’s just plug this into the square of the distance.  Doing this gives,

There is now a single critical point, , and since the second derivative is always positive we know that this point must give the absolute minimum.  So all that we need to do at this point is find the value(s) of x that go with this value of y.

The points are then,

So, for significantly less work we got exactly the same answer.

Suppose that we have a positive function, , that exists everywhere then  and  will have the same critical points and the relative extrema will occur at the same points.