In the previous section we looked at double integrals over
rectangular regions. The problem with
this is that most of the regions are not rectangular so we need to now look at
the following double integral,
where D is any
region.
There are two types of regions that we need to look at. Here is a sketch of both of them.
We will often use set
builder notation to describe these regions.
Here is the definition for the region in Case 1
and here is the definition for the region in Case 2.
This notation is really just a fancy way of saying we are
going to use all the points, 
,
in which both of the coordinates satisfy the two given inequalities.
The double integral for both of these cases are defined in
terms of iterated integrals as follows.
In Case 1 where the integral is defined to be,
In Case 2 where the integral is defined to be,
Here are some properties of the double integral that we
should go over before we actually do some examples. Note that all three of these properties are really
just extensions of properties of single integrals that have been extended to
double integrals.
Properties
|
1.
2. ,
where c is any constant.
3. If the region D can be split into two separate
regions D1 and D2 then the integral can be
written as
|
Let’s take a look at some examples of double integrals over
general regions.
|
Example 1 Evaluate
each of the following integrals over the given region D.
(a) , [Solution]
(b) , D
is the region bounded by and . [Solution]
(c) , D
is the triangle with vertices ,
,
and .
[Solution]
Solution
(a) ,
Okay, this first one is set up to just use the formula above
so let’s do that.
[Return to Problems]
(b) , D is the region bounded by and .
In this case we need to determine the two inequalities for
x and y that we need to do the integral. The best way to do this is the graph the
two curves. Here is a sketch.
So, from the sketch we can see that that two inequalities
are,
We can now do the integral,
[Return to Problems]
(c) , D is the triangle with vertices , , and .
We got even less information about the region this
time. Let’s start this off by
sketching the triangle.
Since we have two points on each edge it is easy to get the
equations for each edge and so we’ll leave it to you to verify the equations.
Now, there are two ways to describe this region. If we use functions of x, as shown in the image we will have to break the region up into
two different pieces since the lower function is different depending upon the
value of x. In this case the region would be given by where,
Note the is the “union” symbol and just means that D is the region we get by combing the
two regions. If we do this then we’ll
need to do two separate integrals, one for each of the regions.
To avoid this we could turn things around and solve the
two equations for x to get,
If we do this we can notice that the same function is
always on the right and the same function is always on the left and so the
region is,
Writing the region in this form means doing a single
integral instead of the two integrals we’d have to do otherwise.
Either way should give the same answer and so we can get
an example in the notes of splitting a region up let’s do both integrals.
Solution 1
That was a lot of work.
Notice however, that after we did the first substitution that we
didn’t multiply everything out. The
two quadratic terms can be easily integrated with a basic Calc I substitution
and so we didn’t bother to multiply them out.
We’ll do that on occasion to make some of these integrals a little easier.
Solution 2
This solution will be a lot less work since we are only
going to do a single integral.
So, the numbers were a little messier, but other than that
there was much less work for the same result.
Also notice that again we didn’t cube out the two terms as they are
easier to deal with using a Calc I substitution.
[Return to Problems]
|
As the last part of the previous example has shown us we can
integrate these integrals in either order (i.e.
x followed by y or y followed by x), although often one order will be
easier than the other. In fact there
will be times when it will not even be possible to do the integral in one order
while it will be possible to do the integral in the other order.
Let’s see a couple of examples of these kinds of integrals.
|
Example 2 Evaluate
the following integrals by first reversing the order of integration.
(a) [Solution]
(b) [Solution]
Solution
(a)
First, notice that if we try to integrate with respect to y we can’t do the integral because we
would need a y2 in front
of the exponential in order to do the y
integration. We are going to hope that
if we reverse the order of integration we will get an integral that we can
do.
Now, when we say that we’re going to reverse the order of
integration this means that we want to integrate with respect to x first and then y. Note as well that we
can’t just interchange the integrals, keeping the original limits, and be
done with it. This would not fix our
original problem and in order to integrate with respect to x we can’t have x’s in the limits of the integrals. Even if we ignored that the answer would
not be a constant as it should be.
So, let’s see how we reverse the order of
integration. The best way to reverse
the order of integration is to first sketch the region given by the original
limits of integration. From the
integral we see that the inequalities that define this region are,
These inequalities tell us that we want the region with on the lower boundary and on the upper boundary that lies between and . Here is a sketch of that region.
Since we want to integrate with respect to x first we will need to determine
limits of x (probably in terms of y) and then get the limits on the y’s.
Here they are for this region.
Any horizontal line drawn in this region will start at and end at and so these are the limits on the x’s and the range of y’s for the regions is 0 to 9.
The integral, with the order reversed, is now,
and notice that we can do the first integration with this
order. We’ll also hope that this will
give us a second integral that we can do.
Here is the work for this integral.
[Return to Problems]
(b)
As with the first
integral we cannot do this integral by integrating with respect to x first so we’ll hope that by
reversing the order of integration we will get something that we can
integrate. Here are the limits for the
variables that we get from this integral.
and here is a sketch of this region.
So, if we reverse the order of integration we get the
following limits.
The integral is then,
[Return to Problems]
|
The final topic of this section is two geometric
interpretations of a double integral.
The first interpretation is an extension of the idea that we used to
develop the idea of a double integral in the first section
of this chapter. We did this by looking
at the volume of the solid that was below the surface of the function and over the rectangle R in the xy-plane. This idea can be extended to more general
regions.
The volume of the solid that lies below the surface given by
and above the region D in the xy-plane is
given by,
|
Example 3 Find
the volume of the solid that lies below the surface given by and lies above the region in the xy-plane bounded by and .
Solution
Here is the graph of the surface and we’ve tried to show
the region in the xy-plane below
the surface.
 
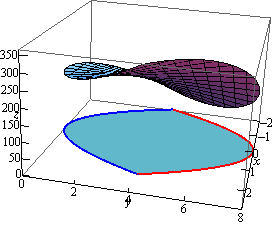
Here is a sketch of the region in the xy-plane by itself.
By setting the two bounding equations equal we can see
that they will intersect at and . So, the inequalities that will define the
region D in the xy-plane are,
The volume is then given by,
|
|
Example 4 Find
the volume of the solid enclosed by the planes ,
,
,
.
Solution This example is a little
different from the previous one. Here
the region D is not explicitly
given so we’re going to have to find it.
First, notice that the last two planes are really telling us that we
won’t go past the xy-plane and the yz-plane when we reach them.
The first plane, ,
is the top of the volume and so we are really looking for the volume under,
and above the region D
in the xy-plane. The second plane, (yes that is a plane), gives one of the
sides of the volume as shown below.
 
The region D
will be the region in the xy-plane
(i.e. ) that is bounded by ,
,
and the line where intersects the xy-plane. We can determine
where intersects the xy-plane by plugging into it.
So, here is a sketch the region D.
The region D is
really where this solid will sit on the xy-plane
and here are the inequalities that define the region.
Here is the volume of this solid.
|
The second geometric interpretation of a double integral is
the following.
This is easy to see why this is true in general. Let’s suppose that we want to find the area
of the region shown below.
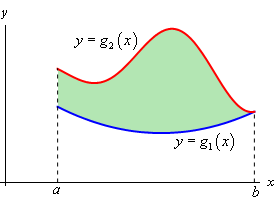
From Calculus I we know that this area can be found by the
integral,
Or in terms of a double integral we have,
This is exactly the same formula we had in Calculus I.