You can navigate through this E-Book using the menu to the left. For E-Books that have a Chapter/Section organization each option in the menu to the left indicates a chapter and will open a menu showing the sections in that chapter. Alternatively, you can navigate to the next/previous section or chapter by clicking the links in the boxes at the very top and bottom of the material.
Also, depending upon the E-Book, it will be possible to download the complete E-Book, the chapter containing the current section and/or the current section. You can do this be clicking on the E-Book, Chapter, and/or the Section link provided below.
For those pages with mathematics on them you can, in most cases, enlarge the mathematics portion by clicking on the equation. Click the enlarged version to hide it.
Inverse Trig Functions
[Show All Solutions]
One of the more common notations for inverse trig functions
can be very confusing. First, regardless
of how you are used to dealing with exponentiation we tend to denote an inverse
trig function with an “exponent” of “-1”.
In other words, the inverse cosine is denoted as 
. It is important here to note that in this
case the “-1” is NOT an exponent and so,
.
In inverse trig functions the “-1” looks like an exponent
but it isn’t, it is simply a notation that we use to denote the fact that we’re
dealing with an inverse trig function.
It is a notation that we use in this case to denote inverse trig
functions. If I had really wanted
exponentiation to denote 1 over cosine I would use the following.
There’s another notation for inverse trig functions that
avoids this ambiguity. It is the
following.
So, be careful with the notation for inverse trig functions!
There are, of course, similar inverse functions for the
remaining three trig functions, but these are the main three that you’ll see in
a calculus class so I’m going to concentrate on them.
To evaluate inverse trig functions remember that the
following statements are equivalent.
In other words, when we evaluate an inverse trig function we
are asking what angle, ,
did we plug into the trig function (regular, not inverse!) to get x.
So, let’s do some problems to see how these work. Evaluate each of the following.
1.
Show Solution
In Problem 1 of the Solving Trig Equations
section we solved the following equation.
In other words, we asked what
angles, t, do we need to plug into
cosine to get ? This is essentially what we are asking here
when we are asked to compute the inverse trig function.
There is one very large difference
however. In Problem 1 we were solving an equation which yielded an
infinite number of solutions. These
were,
In the case of inverse trig
functions we are after a single value.
We don’t want to have to guess at which one of the infinite possible
answers we want. So, to make sure we get
a single value out of the inverse trig cosine function we use the following
restrictions on inverse cosine.
The restriction on the guarantees that we will only get a single
value angle and since we can’t get values of x out of cosine that are larger than 1 or smaller than -1 we also
can’t plug these values into an inverse trig function.
So, using these restrictions on
the solution to Problem 1 we can see that the answer in this case is
2.
Show Solution
In general we don’t need to
actually solve an equation to determine the value of an inverse trig
function. All we need to do is look at a
unit circle. So in this case we’re after
an angle between 0 and for which cosine will take on the value . So, check out the following unit circle
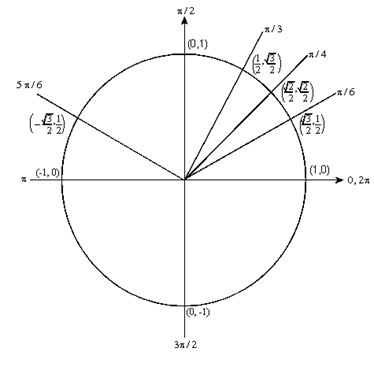
From this we can see that
3.
Show Solution
The restrictions that we put on for the inverse cosine function will not work
for the inverse sine function. Just look
at the unit circle above and you will see that between 0 and there are in fact two angles for which sine
would be and this is not what we want. As with the inverse cosine function we only
want a single value. Therefore, for the
inverse sine function we use the following restrictions.
By checking out the unit circle
we see
4.
Show Solution
5.
Show Solution
Recalling the answer to Problem 1 in this section the solution to this problem is much
easier than it look’s like on the surface.
This problem leads to a couple of
nice facts about inverse cosine
6.
Show Solution
This problem is also not too
difficult (hopefully…).
As with inverse cosine we also
have the following facts about inverse sine.
7. .
Show Solution
Just as inverse cosine and inverse
sine had a couple of nice facts about them so does inverse tangent. Here is the fact
Using this fact makes this a very
easy problem as I couldn’t do by hand!
A calculator could easily do it but I couldn’t get an exact answer from
a unit circle.