You can navigate through this E-Book using the menu to the left. For E-Books that have a Chapter/Section organization each option in the menu to the left indicates a chapter and will open a menu showing the sections in that chapter. Alternatively, you can navigate to the next/previous section or chapter by clicking the links in the boxes at the very top and bottom of the material.
Also, depending upon the E-Book, it will be possible to download the complete E-Book, the chapter containing the current section and/or the current section. You can do this be clicking on the E-Book, Chapter, and/or the Section link provided below.
For those pages with mathematics on them you can, in most cases, enlarge the mathematics portion by clicking on the equation. Click the enlarged version to hide it.
In this section we need to have a brief discussion of vector
arithmetic.
We’ll start with addition
of two vectors. So, given the vectors 
and the addition of the two vectors is given by
the following formula.
The following figure gives the geometric interpretation of
the addition of two vectors.
This is sometimes called the parallelogram law or triangle
law.
Computationally, subtraction
is very similar. Given the vectors and the difference of the two vectors is given by,
Here is the geometric interpretation of the difference of two
vectors.
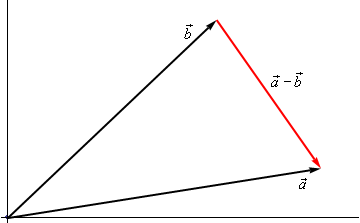
It is a little harder to see this geometric
interpretation. To help see this let’s
instead think of subtraction as the addition of and . First, as we’ll see in a bit is the same vector as with opposite signs on all the
components. In other words, goes in the opposite direction as . Here is the vector set up for .
As we can see from this figure we can move the vector
representing to the position we’ve got in the first figure
showing the difference of the two vectors.
Note that we can’t add or subtract two vectors unless they a
have the same number of components. If
they don’t have the same number of components then addition and subtraction
can’t be done.
The next arithmetic operation that we want to look at is scalar multiplication. Given the vector and any number c the scalar multiplication is,
So, we multiply all the components by the constant c.
To see the geometric interpretation of scalar multiplication let’s take
a look at an example.
|
Example 1 For
the vector compute ,
and . Graph all four vectors on the same axis
system.
Solution
Here are the three scalar multiplications.
Here is the graph for each of these vectors.
|
In the previous example we can see that if c is positive all scalar multiplication
will do is stretch (if ) or shrink (if ) the original vector, but it won’t
change the direction. Likewise, if c is negative scalar multiplication will
switch the direction so that the vector will point in exactly the opposite
direction and it will again stretch or shrink the magnitude of the vector
depending upon the size of c.
There are several nice applications of scalar multiplication
that we should now take a look at.
The first is parallel vectors. This is a concept that we will see quite a
bit over the next couple of sections.
Two vectors are parallel if they have the same direction or are in
exactly opposite directions. Now, recall
again the geometric interpretation of scalar multiplication. When we performed scalar multiplication we
generated new vectors that were parallel to the original vectors (and each
other for that matter).
So, let’s suppose that and are parallel vectors. If they are parallel then there must be a
number c so that,
So, two vectors are parallel if one is a scalar multiple of
the other.
The next application is best seen in an example.
|
Example 3 Find
a unit vector that points in the same direction as .
Solution
Okay, what we’re asking for is a new parallel vector
(points in the same direction) that happens to be a unit vector. We can do this with a scalar multiplication
since all scalar multiplication does is change the length of the original
vector (along with possibly flipping the direction to the opposite
direction).
Here’s what we’ll do.
First let’s determine the magnitude of .
Now, let’s form the following new vector,
The claim is that this is a unit vector. That’s easy enough to check
This vector also points in the same direction as since it is only a scalar multiple of and we used a positive multiple.
|
So, in general, given a vector ,
will be a unit vector that points in the same
direction as .
Standard Basis
Vectors Revisited
In the previous section we introduced the idea of standard
basis vectors without really discussing why they were important. We can now do that. Let’s start with the vector
We can use the addition of vectors to break this up as
follows,
Using scalar multiplication we can further rewrite the
vector as,
Finally, notice that these three new vectors are simply the
three standard basis vectors for three dimensional space.
So, we can take any vector and write it in terms of the
standard basis vectors. From this point
on we will use the two notations interchangeably so make sure that you can deal
with both notations.