In this section we are going to take a look at two fairly
important problems in the study of calculus.
There are two reasons for looking at these problems now.
First, both of these problems will lead us into the study of
limits, which is the topic of this chapter after all. Looking at these problems here will allow us
to start to understand just what a limit is and what it can tell us about a
function.
Secondly, the rate of change problem that we’re going to be
looking at is one of the most important concepts that we’ll encounter in the
second chapter of this course. In fact,
it’s probably one of the most important concepts that we’ll encounter in the
whole course. So looking at it now will
get us to start thinking about it from the very beginning.
Tangent Lines
The first problem that we’re going to take a look at is the
tangent line problem. Before getting
into this problem it would probably be best to define a tangent line.
A tangent line to the function f(x) at the point 
is a line that just touches the graph of the
function at the point in question and is “parallel” (in some way) to the graph
at that point. Take a look at the graph
below.
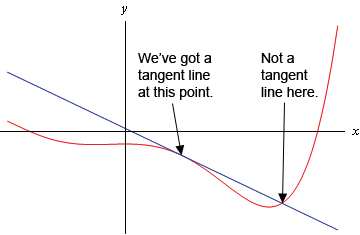
In this graph the line is a tangent line at the indicated
point because it just touches the graph at that point and is also “parallel” to
the graph at that point. Likewise, at
the second point shown, the line does just touch the graph at that point, but
it is not “parallel” to the graph at that point and so it’s not a tangent line
to the graph at that point.
At the second point shown (the point where the line isn’t a
tangent line) we will sometimes call the line a secant line.
We’ve used the word parallel a couple of times now and we
should probably be a little careful with it.
In general, we will think of a line and a graph as being parallel at a
point if they are both moving in the same direction at that point. So, in the first point above the graph and
the line are moving in the same direction and so we will say they are parallel
at that point. At the second point, on
the other hand, the line and the graph are not moving in the same direction and
so they aren’t parallel at that point.
Okay, now that we’ve gotten the definition of a tangent line
out of the way let’s move on to the tangent line problem. That’s probably best done with an example.
|
Example 1 Find
the tangent line to at x =
1.
Solution
We know from algebra that to find the equation of a line
we need either two points on the line or a single point on the line and the
slope of the line. Since we know that
we are after a tangent line we do have a point that is on the line. The tangent line and the graph of the
function must touch at x = 1 so the
point must be on the line.
Now we reach the problem.
This is all that we know about the tangent line. In order to find the tangent line we need
either a second point or the slope of the tangent line. Since the only reason for needing a second
point is to allow us to find the slope of the tangent line let’s just
concentrate on seeing if we can determine the slope of the tangent line.
At this point in time all that we’re going to be able to
do is to get an estimate for the slope of the tangent line, but if we do it
correctly we should be able to get an estimate that is in fact the actual
slope of the tangent line. We’ll do
this by starting with the point that we’re after, let’s call it . We will then pick another point that lies
on the graph of the function, let’s call that point .
For the sake of argument let’s take choose and so the second point will be . Below is a graph of the function, the
tangent line and the secant line that connects P and Q.
We can see from this graph that the secant and tangent
lines are somewhat similar and so the slope of the secant line should be
somewhat close to the actual slope of the tangent line. So, as an estimate of the slope of the
tangent line we can use the slope of the secant line, let’s call it ,
which is,
Now, if we weren’t too interested in accuracy we could say
this is good enough and use this as an estimate of the slope of the tangent
line. However, we would like an
estimate that is at least somewhat close the actual value. So, to get a better estimate we can take an
x that is closer to and redo the work above to get a new
estimate on the slope. We could then
take a third value of x even closer
yet and get an even better estimate.
In other words, as we take Q closer and closer to P
the slope of the secant line connecting Q
and P should be getting closer and
closer to the slope of the tangent line.
If you are viewing this on the web, the image below shows this
process.
As you can see (if you’re reading this on the web) as we
moved Q in closer and closer to P the secant lines does start to look
more and more like the tangent line and so the approximate slopes (i.e. the slopes of the secant lines)
are getting closer and closer to the exact slope. Also, do not worry about how I got the
exact or approximate slopes. We’ll be
computing the approximate slopes shortly and we’ll be able to compute the
exact slope in a few sections.
In this figure we only looked at Q’s that were to the right of P, but we could have just as easily used Q’s that were to the left of P and we would have received the same
results. In fact, we should always
take a look at Q’s that are on both
sides of P. In this case the same thing is happening on
both sides of P. However, we will eventually see that
doesn’t have to happen. Therefore we
should always take a look at what is happening on both sides of the point in
question when doing this kind of process.
So, let’s see if we can come up with the approximate
slopes I showed above, and hence an estimation of the slope of the tangent
line. In order to simplify the process
a little let’s get a formula for the slope of the line between P and Q, ,
that will work for any x that we
choose to work with. We can get a
formula by finding the slope between P
and Q using the “general” form of .
Now, let’s pick some values of x getting closer and closer to ,
plug in and get some slopes.
|
x
|
|
x
|
|
|
2
|
-6
|
0
|
-2
|
|
1.5
|
-5
|
0.5
|
-3
|
|
1.1
|
-4.2
|
0.9
|
-3.8
|
|
1.01
|
-4.02
|
0.99
|
-3.98
|
|
1.001
|
-4.002
|
0.999
|
-3.998
|
|
1.0001
|
-4.0002
|
0.9999
|
-3.9998
|
So, if we take x’s to
the right of 1 and move them in very close to 1 it appears that the slope of
the secant lines appears to be approaching -4. Likewise, if we take x’s to the left of 1 and move them in very
close to 1 the slope of the secant lines again appears to be approaching -4.
Based on this evidence it seems that the slopes of the
secant lines are approaching -4 as we move in towards ,
so we will estimate that the slope of the tangent line is also -4. As noted above, this is the correct value
and we will be able to prove this eventually.
Now, the equation of the line that goes through is given by
Therefore, the equation of the tangent line to at x = 1
is
|
There are a couple of important points to note about our
work above. First, we looked at points
that were on both sides of . In this kind of process it is important to
never assume that what is happening on one side of a point will also be
happening on the other side as well. We
should always look at what is happening on both sides of the point. In this example we could sketch a graph and
from that guess that what is happening on one side will also be happening on
the other, but we will usually not have the graphs in front of us or be able to
easily get them.
Next, notice that when we say we’re going to move in close
to the point in question we do mean that we’re going to move in very close and
we also used more than just a couple of points.
We should never try to determine a trend based on a couple of points
that aren’t really all that close to the point in question.
The next thing to notice is really a warning more than
anything. The values of in this example were fairly “nice” and it was
pretty clear what value they were approaching after a couple of
computations. In most cases this will
not be the case. Most values will be far
“messier” and you’ll often need quite a few computations to be able to get an
estimate.
Last, we were after something that was happening at and we couldn’t actually plug into our formula for the slope. Despite this limitation we were able to
determine some information about what was happening at simply by looking at what was happening around
. This is more important than you might at
first realize and we will be discussing this point in detail in later sections.
Before moving on let’s do a quick review of just what we did
in the above example. We wanted the
tangent line to at a point . First, we know that the point will be on the tangent line. Next, we’ll take a second point that is on
the graph of the function, call it and compute the slope of the line connecting P and Q as follows,
We then take values of x
that get closer and closer to (making sure to look at x’s on both sides of and use this list of values to estimate the
slope of the tangent line, m.
The tangent line will then be,
Rates of Change
The next problem that we need to look at is the rate of
change problem. This will turn out to be
one of the most important concepts that we will look at throughout this course.
Here we are going to consider a function, f(x), that represents some quantity that
varies as x varies. For instance, maybe f(x) represents the amount of water in a holding tank after x minutes. Or maybe f(x)
is the distance traveled by a car after x
hours. In both of these example we used x to represent time. Of course x
doesn’t have to represent time, but it makes for examples that are easy to
visualize.
What we want to do here is determine just how fast f(x) is changing at some point, say . This is called the instantaneous rate of change or sometimes just rate of change of f(x) at
.
As with the tangent line problem all that we’re going to be
able to do at this point is to estimate the rate of change. So let’s continue with the examples above and
think of f(x) as something that is
changing in time and x being the time
measurement. Again x doesn’t have to represent time but it will make the explanation a
little easier. While we can’t compute
the instantaneous rate of change at this point we can find the average rate of
change.
To compute the average rate of change of f(x) at all we need to do is to choose another point,
say x, and then the average rate of
change will be,
Then to estimate the instantaneous rate of change at all we need to do is to choose values
of x getting closer and closer to (don’t forget to chose them on both sides of ) and compute values of A.R.C.
We can then estimate the instantaneous rate of change from that.
Let’s take a look at an example.
|
Example 2 Suppose
that the amount of air in a balloon after t
hours is given by
Estimate the instantaneous rate of change of the volume
after 5 hours.
Solution
Okay. The first
thing that we need to do is get a formula for the average rate of change of
the volume. In this case this is,
To estimate the instantaneous rate of change of the volume
at we just need to pick values of t that are getting closer and closer
to . Here is a table of values of t and the average rate of change for
those values.
|
t
|
A.R.C.
|
t
|
A.R.C.
|
|
6
|
25.0
|
4
|
7.0
|
|
5.5
|
19.75
|
4.5
|
10.75
|
|
5.1
|
15.91
|
4.9
|
14.11
|
|
5.01
|
15.0901
|
4.99
|
14.9101
|
|
5.001
|
15.009001
|
4.999
|
14.991001
|
|
5.0001
|
15.00090001
|
4.9999
|
14.99910001
|
So, from this table it looks like the average rate of
change is approaching 15 and so we can estimate that the instantaneous rate
of change is 15 at this point.
|
So, just what does this tell us about the volume at this
point? Let’s put some units on the
answer from above. This might help us to
see what is happening to the volume at this point. Let’s suppose that the units on the volume
were in cm3. The units on the
rate of change (both average and instantaneous) are then cm3/hr.
We have estimated that at the volume is changing at a rate of 15 cm3/hr. This means that at the volume is changing in such a way that, if
the rate were constant, then an hour later there would be 15 cm3
more air in the balloon than there was at .
We do need to be careful here however. In reality there probably won’t be 15 cm3
more air in the balloon after an hour.
The rate at which the volume is changing is generally not constant and
so we can’t make any real determination as to what the volume will be in
another hour. What we can say is that
the volume is increasing, since the instantaneous rate of change is positive,
and if we had rates of change for other values of t we could compare the numbers and see if the rate of change is
faster or slower at the other points.
For instance, at the instantaneous rate of change is 0 cm3/hr
and at the instantaneous rate of change is -9 cm3/hr. I’ll leave it to you to check these rates of
change. In fact, that would be a good
exercise to see if you can build a table of values that will support my claims
on these rates of change.
Anyway, back to the example.
At the rate of change is zero and so at this
point in time the volume is not changing at all. That doesn’t mean that it will not change in
the future. It just means that exactly
at the volume isn’t changing. Likewise at the volume is decreasing since the rate of
change at that point is negative. We can
also say that, regardless of the increasing/decreasing aspects of the rate of
change, the volume of the balloon is changing faster at than it is at since 15 is larger than 9.
We will be talking a lot more about rates of change when we
get into the next chapter.
Velocity Problem
Let’s briefly look at the velocity problem. Many calculus books will treat this as its
own problem. I however, like to think of
this as a special case of the rate of change problem. In the velocity problem we are given a
position function of an object, f(t),
that gives the position of an object at time t. Then to compute the
instantaneous velocity of the object we just need to recall that the velocity
is nothing more than the rate at which the position is changing.
In other words, to estimate the instantaneous velocity we
would first compute the average velocity,
and then take values of t
closer and closer to and use these values to estimate the
instantaneous velocity.
Change of Notation
There is one last thing that we need to do in this section
before we move on. The main point of
this section was to introduce us to a couple of key concepts and ideas that we
will see throughout the first portion of this course as well as get us started
down the path towards limits.
Before we move into limits officially let’s go back and do a
little work that will relate both (or all three if you include velocity as a
separate problem) problems to a more general concept.
First, notice that whether we wanted the tangent line,
instantaneous rate of change, or instantaneous velocity each of these came down
to using exactly the same formula.
Namely,
This should suggest that all three of these problems are
then really the same problem. In fact
this is the case as we will see in the next chapter. We are really working the same problem in
each of these cases the only difference is the interpretation of the
results.
In preparation for the next section where we will discuss
this in much more detail we need to do a quick change of notation. It’s easier to do here since we’ve already
invested a fair amount of time into these problems.
In all of these problems we wanted to determine what was
happening at . To do this we chose another value of x and plugged into (1). For what we were doing here that is probably
most intuitive way of doing it. However,
when we start looking at these problems as a single problem (1)
will not be the best formula to work with.
What we’ll do instead is to first determine how far from we want to move and then define our new point
based on that decision. So, if we want
to move a distance of h from the new point would be .
As we saw in our work above it is important to take values
of x that are both sides of .
This way of choosing new value of x will
do this for us. If h>0 we will get value of x
that are to the right of and if h<0
we will get values of x that are to
the left of .
Now, with this new way of getting a second x, (1)
will become,
On the surface it might seem that (2) is
going to be an overly complicated way of dealing with this stuff. However, as we will see it will often be
easier to deal with (2)
than it will be to deal with (1).