Section 3.11 : Related Rates
In this section we are going to look at an application of implicit differentiation. Most of the applications of derivatives are in the next chapter however there are a couple of reasons for placing it in this chapter as opposed to putting it into the next chapter with the other applications. The first reason is that it’s an application of implicit differentiation and so putting it right after that section means that we won’t have forgotten how to do implicit differentiation. The other reason is simply that after doing all these derivatives we need to be reminded that there really are actual applications to derivatives. Sometimes it is easy to forget there really is a reason that we’re spending all this time on derivatives.
For these related rates problems, it’s usually best to just jump right into some problems and see how they work.
The first thing that we’ll need to do here is to identify what information that we’ve been given and what we want to find. Before we do that let’s notice that both the volume of the balloon and the radius of the balloon will vary with time and so are really functions of time, i.e. \(V\left( t \right)\) and \(r\left( t \right)\).
We know that air is being pumped into the balloon at a rate of 5 cm3/min. This is the rate at which the volume is increasing. Recall that rates of change are nothing more than derivatives and so we know that,
\[V'\left( t \right) = 5\]We want to determine the rate at which the radius is changing. Again, rates are derivatives and so it looks like we want to determine,
\[r'\left( t \right) = ?\hspace{0.25in}{\rm{when}}\hspace{0.25in}r\left( t \right) = \frac{d}{2} = 10\,{\rm{cm}}\]Note that we needed to convert the diameter to a radius.
Now that we’ve identified what we have been given and what we want to find we need to relate these two quantities to each other. In this case we can relate the volume and the radius with the formula for the volume of a sphere.
\[V\left( t \right) = \frac{4}{3}\pi {\left[ {r\left( t \right)} \right]^3}\]As in the previous section when we looked at implicit differentiation, we will typically not use the \(\left( t \right)\) part of things in the formulas, but since this is the first time through one of these we will do that to remind ourselves that they are really functions of \(t\).
Now we don’t really want a relationship between the volume and the radius. What we really want is a relationship between their derivatives. We can do this by differentiating both sides with respect to \(t\). In other words, we will need to do implicit differentiation on the above formula. Doing this gives,
\[V' = 4\pi {r^2}r'\]Note that at this point we went ahead and dropped the \(\left( t \right)\) from each of the terms. Now all that we need to do is plug in what we know and solve for what we want to find.
\[5 = 4\pi \left( {{{10}^2}} \right)r'\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}r' = \frac{1}{{80\pi }}\,{\rm{ cm/min}}\]We can get the units of the derivative by recalling that,
\[r' = \frac{{dr}}{{dt}}\]The units of the derivative will be the units of the numerator (cm in the previous example) divided by the units of the denominator (min in the previous example).
Let’s work some more examples.
The first thing to do in this case is to sketch picture that shows us what is going on.

We’ve defined the distance of the bottom of the ladder from the wall to be \(x\) and the distance of the top of the ladder from the floor to be \(y\). Note as well that these are changing with time and so we really should write \(x\left( t \right)\) and \(y\left( t \right)\). However, as is often the case with related rates/implicit differentiation problems we don’t write the \(\left( t \right)\) part just try to remember this in our heads as we proceed with the problem.
Next, we need to identify what we know and what we want to find. We know that the rate at which the bottom of the ladder is moving towards the wall. This is,
\[x' = - \frac{1}{4}\]Note as well that the rate is negative since the distance from the wall, \(x\), is decreasing. We always need to be careful with signs with these problems.
We want to find the rate at which the top of the ladder is moving away from the floor. This is \(y'\). Note as well that this quantity should be positive since \(y\) will be increasing.
As with the first example we first need a relationship between \(x\) and \(y\). We can get this using Pythagorean theorem.
\[{x^2} + {y^2} = {\left( {15} \right)^2} = 225\]All that we need to do at this point is to differentiate both sides with respect to \(t\), remembering that \(x\) and \(y\) are really functions of \(t\) and so we’ll need to do implicit differentiation. Doing this gives an equation that shows the relationship between the derivatives.
\[\begin{equation}2xx' + 2yy' = 0\end{equation} \label{eq:eq1}\]Next, let’s see which of the various parts of this equation that we know and what we need to find. We know \(x'\) and are being asked to determine \(y'\) so it’s okay that we don’t know that. However, we still need to determine \(x\) and \(y\).
Determining \(x\) and \(y\) is actually fairly simple. We know that initially \(x = 10\) and the end is being pushed in towards the wall at a rate of \({\textstyle{1 \over 4}}\)ft/sec and that we are interested in what has happened after 12 seconds. We know that,
\[\begin{align*}{\rm{distance}} = {\rm{rate}} \times {\rm{time}}\\ & = \left( {\frac{1}{4}} \right)\left( {12} \right) = 3\end{align*}\]So, the end of the ladder has been pushed in 3 feet and so after 12 seconds we must have \(x = 7\). Note that we could have computed this in one step as follows,
\[x = 10 - \frac{1}{4}\left( {12} \right) = 7\]To find \(y\) (after 12 seconds) all that we need to do is reuse the Pythagorean Theorem with the values of \(x\) that we just found above.
\[y = \sqrt {225 - {x^2}} = \sqrt {225 - 49} = \sqrt {176} \]Now all that we need to do is plug into \(\eqref{eq:eq1}\) and solve for \(y'\).
\[2\left( 7 \right)\left( -\frac{1}{4} \right)+2\left( \sqrt{176} \right){y}'=0\Rightarrow {y}'=\frac{{}^{7}/{}_{4}}{\sqrt{176}}=\frac{7}{4\sqrt{176}}=0.1319\,\,\text{ft/sec}\]Notice that we got the correct sign for \(y'\). If we’d gotten a negative value we’d have known that we had made a mistake and we could go back and look for it.
Before working another example, we need to make a comment about the set up of the previous problem. When we labeled our sketch, we acknowledged that the hypotenuse is constant and so just called it 15 ft. A common mistake that students will sometimes make here is to also label the hypotenuse as a letter, say \(z\), in this case.
Well, it’s not really a mistake to label with a letter, but it will often lead to problem down the road. Had we labeled the hypotenuse \(z\) then the Pythagorean theorem and its derivative would have been,
\[{x^2} + {y^2} = {z^2}\hspace{0.25in} \to \hspace{0.25in} 2xx' + 2yy' = 2zz'\]Again, there is nothing wrong with doing this but it does require that we acknowledge the values of two more quantities, \(z\) and \(z'\). Because \(z\) is just the hypotenuse that is clearly \(z = 15\). The problem that some students then sometimes run into is determining the value of \(z'\). In this case, we have to remember that because the ladder, and hence the hypotenuse has a fixed length, its length can’t be changing and so \(z' = 0\).
Plugging both of these values into the derivative give us same equation that we got in the example but required a little more effort to get to. It would have been easier to just label the hypotenuse 15 to start off with and not have to worry about remembering that \(z' = 0\).
When labeling a fixed quantity (the length of the ladder in this example) with a letter it is sometimes easy to forget that it is a fixed quantity and so it’s derivative must be zero. If you don’t remember this, the problem becomes impossible to finish as you will have two unknown quantities that you have to deal with. In any problem were a quantity is fixed and will never over the course of the problem change it is always best to just acknowledge that and label it with its value rather than with a letter.
Of course, if we’d had a sliding ladder that was allowed to change length then we would have to label it with a letter. However, for that kind of problem we would also need some more information in the problem statement in order to actually do the problem. The practice problems in this section have several problems in which all three sides of a right triangle are changing. You should check them out and see if you can work them.

This example is not as tricky as it might at first appear. Let’s call the distance between them at any point in time \(x\) as noted above. We can then relate all the known quantities by one of two trig formulas.
\[\cos \theta = \frac{{50}}{x}\hspace{0.25in}\hspace{0.25in}\sec \theta = \frac{x}{{50}}\]We want to find \(x'\)and we could find \(x\) if we wanted to at the point in question using cosine since we also know the angle at that point in time. However, if we use the second formula we won’t need to know \(x\) as you’ll see. So, let’s differentiate that formula.
\[\sec \theta \tan \theta \,\,\theta ' = \frac{{x'}}{{50}}\]As noted, there are no \(x\)’s in this formula. We want to determine \(x'\) and we know that \(\theta = 0.5\) and \(\theta ' = 0.01\) (do you agree with it being positive?). So, just plug in and solve.
\[\left( {50} \right)\left( {0.01} \right)\sec \left( {0.5} \right)\tan \left( {0.5} \right) = x'\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}x' = 0.311254\,\,{\rm{ft}}/\min \]So far we we’ve seen three related rates problems. While each one was worked in a very different manner the process was essentially the same in each. In each problem we identified what we were given and what we wanted to find. We next wrote down a relationship between all the various quantities and used implicit differentiation to arrive at a relationship between the various derivatives in the problem. Finally, we plugged the known quantities into the equation to find the value we were after.
So, in a general sense each problem was worked in pretty much the same manner. The only real difference between them was coming up with the relationship between the known and unknown quantities. This is often the hardest part of the problem. In many problems the best way to come up with the relationship is to sketch a diagram that shows the situation. This often seems like a silly step but can make all the difference in whether we can find the relationship or not.
Let’s work another problem that uses some different ideas and shows some of the different kinds of things that can show up in related rates problems.
- At what rate is the depth of the water in the tank changing when the depth of the water is 6 ft?
- At what rate is the radius of the top of the water in the tank changing when the depth of the water is 6 ft?
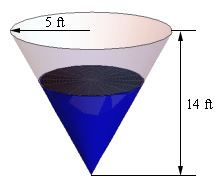
Okay, we should probably start off with a quick sketch (probably not to scale) of what is going on here. We’ll also be doing the sketch as if we were looking at the tank from directly in front of it (and so the 3D of the tank will not be visible) as this will help a little with seeing what is going on. Showing the 3D nature of the tank is liable to just get in the way. So here is the sketch of the tank with some water in it.
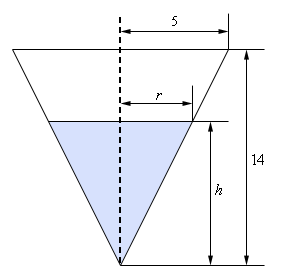
As we can see, the water in the tank actually forms a smaller cone/triangle (depending on which image we are looking at) with the same central angle as the tank itself. The radius of the “water” cone at any time is given by \(r\) and the height of the “water” cone at any time is given by \(h\). The volume of water in the tank at any time \(t\) is given by,
\[V = \frac{1}{3}\pi {r^2}h\]and we’ve been given that \(V' = - 2\).
a At what rate is the depth of the water in the tank changing when the depth of the water is 6 ft? Show Solution
For this part we need to determine \(h'\) when \(h = 6\) and now we have a problem. The only formula that we’ve got that will relate the volume to the height also includes the radius and so if we were to differentiate this with respect to \(t\) we would get,
\[V' = \frac{2}{3}\pi rr'h + \frac{1}{3}\pi {r^2}h'\]So, in this equation we know \(V'\) and \(h\) and want to find \(h'\), but we don’t know \(r\) and \(r'\). As we’ll see finding \(r\) isn’t too bad, but we just don’t have enough information, at this point, that will allow us to find \(r'\) and \(h'\) simultaneously.
To fix this we’ll need to eliminate the \(r\) from the volume formula in some way. This is actually easier than it might at first look. If we go back to our sketch above and look at just the right half of the tank we see that we have two similar triangles and when we say similar we mean similar in the geometric sense. Recall that two triangles are called similar if their angles are identical, which is the case here. When we have two similar triangles then ratios of any two sides will be equal. For our set this means that we have,
\[\frac{r}{h} = \frac{5}{{14}}\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}r = \frac{5}{{14}}h\]If we take this and plug it into our volume formula we have,
\[V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {\left( {\frac{5}{{14}}h} \right)^2}h = \frac{{25}}{{588}}\pi {h^3}\]This gives us a volume formula that only involved the volume and the height of the water. Note however that this volume formula is only valid for our cone, so don’t be tempted to use it for other cones! If we now differentiate this we have,
\[V'\, = \frac{{25}}{{196}}\pi {h^2}h'\]At this point all we need to do is plug in what we know and solve for \(h'\).
\[ - 2 = \frac{{25}}{{196}}\pi \left( {{6^2}} \right)h'\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}h' = \frac{{ - 98}}{{225\pi }} = - 0.1386\]So, it looks like the height is decreasing at a rate of 0.1386 ft/hr.
b At what rate is the radius of the top of the water in the tank changing when the depth of the water is 6 ft? Show Solution
In this case we are asking for \(r'\) and there is an easy way to do this part and a difficult (well, more difficult than the easy way anyway….) way to do it. The “difficult” way is to redo the work in part (a) above only this time use,
\[\frac{h}{r} = \frac{{14}}{5}\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}h = \frac{{14}}{5}r\]to get the volume in terms of \(V\) and \(r\) and then proceed as before.
That’s not terribly difficult, but it is more work that we need to so. Recall from the first part that we have,
\[r = \frac{5}{{14}}h\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}r' = \frac{5}{{14}}h'\]So, as we can see if we take the relationship that relates \(r\) and \(h\) that we used in the first part and differentiate it we get a relationship between \(r'\) and \(h'\). At this point all we need to do here is use the result from the first part to get,
\[r' = \frac{5}{{14}}\left( {\frac{{ - 98}}{{225\pi }}} \right) = - \frac{7}{{45\pi }} = - 0.04951\]Much easier that redoing all of the first part. Note however, that we were only able to do this the “easier” way because it was asking for \(r'\)at exactly the same time that we asked for \(h'\) in the first part. If we hadn’t been using the same time then we would have had no choice but to do this the “difficult” way.
In the second part of the previous problem we saw an important idea in dealing with related rates. In order to find the asked for rate all we need is an equation that relates the rate we’re looking for to a rate that we already know. Sometimes there are multiple equations that we can use and sometimes one will be easier than another.
Also, this problem showed us that we will often have an equation that contains more variables that we have information about and so, in these cases, we will need to eliminate one (or more) of the variables. In this problem we eliminated the extra variable using the idea of similar triangles. This will not always be how we do this, but many of these problems do use similar triangles so make sure you can use that idea.
Let’s work some more problems.

Note that an isosceles triangle is just a triangle in which two of the sides are the same length. In our case sides of the tank have the same length.
Let’s add in some dimensions for the water to the sketch from above.

Now, in this problem we know that \(V' = 6 \mbox{m}^{3}\mbox{/sec}\) and we want to determine \(h'\) when \(h = 1.2\,{\rm{m}}\). Note that because \(V'\) is in terms of meters we need to convert \(h\) into meters as well. So, we need an equation that will relate these two quantities and the volume of the tank will do it.
The volume of this kind of tank is simple to compute. The volume is the area of the end times the depth. For our case the volume of the water in the tank is,
\[\begin{align*}V &= \left( {{\mbox{Area of End}}} \right)\left( {{\rm{depth}}} \right)\\ & = \left( {{\textstyle{1 \over 2}}{\rm{base}} \times {\rm{height}}} \right)\left( {{\rm{depth}}} \right)\\ & = {\textstyle{1 \over 2}}hw\left( 8 \right)\\ & = 4hw\end{align*}\]As with the previous example we’ve got an extra quantity here, \(w\), that is also changing with time and so we need to eliminate it from the problem. To do this we’ll again make use of the idea of similar triangles. If we look at the end of the tank we’ll see that we again have two similar triangles. One for the tank itself and one formed by the water in the tank. Again, remember that with similar triangles ratios of sides must be equal. In our case we’ll use,
\[\frac{w}{5} = \frac{h}{2}\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}w = \frac{5}{2}h\]Plugging this into the volume gives a formula for the volume (and only for this tank) that only involved the height of the water.
\[V = 4hw = 4h\left( {\frac{5}{2}h} \right) = 10{h^2}\]We can now differentiate this to get,
\[V' = 20hh'\]Finally, all we need to do is plug in and solve for \(h'\).
\[6 = 20\left( {1.2} \right)h'\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}h' = 0.25\,\,{\rm{m/sec}}\]So, the height of the water is rising at a rate of 0.25 m/sec.
In order to answer the second part of this question is not all that difficult.
We will need \(w'\) to answer this part and we have the following equation from the similar triangle that relate the width to the height and we can quickly differentiate it to get a relationship between \(w'\) and \(h'\).
\[w = \frac{5}{2}h\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}w' = \frac{5}{2}h'\]From the first part we know the value of \(h'\) and so all wee need to do is plug that into this equation and we’ll have the answer.
\[w' = \frac{5}{2}\left( {0.25} \right) = 0.625\,\,{\rm{m/sec}}\]Therefore the width is increasing at a rate of 0.625 m/sec.
- At what rate is the tip of the shadow moving away from the pole when the person is 25 ft from the pole?
- At what rate is the tip of the shadow moving away from the person when the person is 25 ft from the pole?
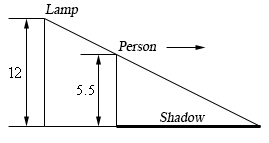
Let’s start off with putting all the relevant quantities into the sketch from above.

Here \(x\) is the distance of the tip of the shadow from the pole, \({x_p}\) is the distance of the person from the pole and \({x_s}\) is the length of the shadow. Also note that we converted the persons height over to 5.5 feet since all the other measurements are in feet.
The tip of the shadow is defined by the rays of light just getting past the person and so we can see they form a set of similar triangles. This will be useful down the road.
a At what rate is the tip of the shadow moving away from the pole when the person is 25 ft from the pole? Show Solution
In this case we want to determine \(x'\) when \({x_p} = 25\) given that \({x'_p} = 2\).
The equation we’ll need here is,
\[x = {x_p} + {x_s}\]but we’ll need to eliminate \({x_s}\) from the equation in order to get an answer. To do this we can again make use of the fact that the two triangles are similar to get,
\[\frac{{5.5}}{{12}} = \frac{{{x_s}}}{x}\hspace{0.25in}\hspace{0.25in}{\rm{Note : }}\frac{{5.5}}{{12}} = \frac{{{\textstyle{{11} \over 2}}}}{{12}} = \frac{{11}}{{24}}\]From this we can quickly see that,
\[{x_s} = \frac{{11}}{{24}}x\]We can then plug this into the equation above and solve for \(x\) as follows.
\[x = {x_p} + {x_s} = {x_p} + \frac{{11}}{{24}}x\hspace{0.25in} \Rightarrow \hspace{0.25in} x = \frac{{24}}{{13}}{x_p}\]Now all that we need to do is differentiate this, plug in and solve for \(x'\).
\[x' = \frac{{24}}{{13}}{x'_p}\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}x' = \frac{{24}}{{13}}\left( 2 \right) = 3.6923{\rm{ ft/sec}}\]The tip of the shadow is then moving away from the pole at a rate of 3.6923 ft/sec. Notice as well that we never actually had to use the fact that \({x_p} = 25\) for this problem. That will happen on rare occasions.
b At what rate is the tip of the shadow moving away from the person when the person is 25 ft from the pole? Show Solution
This part is actually quite simple if we have the answer from (a) in hand, which we do of course. In this case we know that \({x_s}\) represents the length of the shadow, or the distance of the tip of the shadow from the person so it looks like we want to determine \({x'_s}\) when \({x_p} = 25\).
Again, we can use \(x = {x_p} + {x_s}\), however unlike the first part we now know that \({x'_p} = 2\) and \(x' = 3.6923{\rm{ ft/sec}}\) so in this case all we need to do is differentiate the equation and plug in for all the known quantities.
\[\begin{align*}x' &= {{x'}_p} + {{x'}_s}\\ 3.6923 &= 2 + {{x'}_s}\hspace{0.5in}{{x'}_s} = 1.6923{\rm{ ft/sec}}\end{align*}\]The tip of the shadow is then moving away from the person at a rate of 1.6923 ft/sec.

Below is a copy of the sketch in the problem statement with all the relevant quantities added in. The top of the shadow will be defined by the light rays going over the head of the person and so we again get yet another set of similar triangles.

In this case we want to determine \(y'\) when the person is 8 ft from wall or \(x = 12{\rm{ ft}}\). Also, if the person is moving towards the wall at 2.5 ft/sec then the person must be moving away from the spotlight at 2.5 ft/sec and so we also know that \(x' = 2.5\).
In all the previous problems that used similar triangles we used the similar triangles to eliminate one of the variables from the equation we were working with. In this case however, we can get the equation that relates \(x\) and \(y\) directly from the two similar triangles. In this case the equation we’re going to work with is,
\[\frac{y}{6} = \frac{{20}}{x}\hspace{0.25in}\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}y = \frac{{120}}{x}\]Now all that we need to do is differentiate and plug values into solve to get \(y'\).
\[y' = - \frac{{120}}{{{x^2}}}x'\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}y' = - \frac{{120}}{{{{12}^2}}}\left( {2.5} \right) = - 2.0833{\rm{ ft/sec}}\]The height of the shadow is then decreasing at a rate of 2.0833 ft/sec.
Okay, we’ve worked quite a few problems now that involved similar triangles in one form or another so make sure you can do these kinds of problems.
It’s now time to do a problem that while similar to some of the problems we’ve done to this point is also sufficiently different that it can cause problems until you’ve seen how to do it.

There is a lot to digest here with this problem. Let’s start off with a sketch of the situation that shows each person’s location sometime after both people start riding.

Now we are after \(z'\) and we know that \(x' = 5\) and \(y' = 3\). We want to know \(z'\) after Person A had been riding for 25 minutes and Person B has been riding for \(25 - 7 = 18\) minutes. After converting these times to seconds (because our rates are all in m/sec) this means that at the time we’re interested in each of the bike riders has rode,
\[x = 5\left( {25 \times 60} \right) = 7500{\rm{ m}}\hspace{0.25in}\hspace{0.25in}y = 3\left( {18 \times 60} \right) = 3240{\rm{ m}}\]Next, the Pythagorean theorem tells us that,
\[\begin{equation}{z^2} = {\left( {x + y} \right)^2} + {350^2}\label{eq:eq2}\end{equation}\]Therefore, 25 minutes after Person A starts riding the two bike riders are
\[z = \sqrt {{{\left( {x + y} \right)}^2} + {{350}^2}} = \sqrt {{{\left( {7500 + 3240} \right)}^2} + {{350}^2}} = 10745.7015\,\,{\rm{m}}\]apart.
To determine the rate at which the two riders are moving apart all we need to do then is differentiate \(\eqref{eq:eq2}\) and plug in all the quantities that we know to find \(z'\).
\[\begin{align*}2zz' & = 2\left( {x + y} \right)\left( {x' + y'} \right)\\ 2\left( {10745.7015} \right)z' & = 2\left( {7500 + 3240} \right)\left( {5 + 3} \right)\\ z' & = 7.9958{\rm{ m/sec}}\end{align*}\]So, the two riders are moving apart at a rate of 7.9958 m/sec.
Every problem that we’ve worked to this point has come down to needing a geometric formula and we should probably work a quick problem that is not geometric in nature.
Suppose that \({R_{\,1}}\) is increasing at a rate of 0.4 \(\Omega \)/min and \({R_{\,2}}\) is decreasing at a rate of 0.7\(\Omega \)/min. At what rate is \(R\) changing when \({R_{\,1}} = 80\,\Omega \) and \({R_{\,2}} = 105\,\Omega \)?
Okay, unlike the previous problems there really isn’t a whole lot to do here. First, let’s note that we’re looking for \(R'\) and that we know \({R'_{\,1}} = 0.4\) and \({R'_{\,2}} = - 0.7\). Be careful with the signs here.
Also, since we’ll eventually need it let’s determine \(R\) at the time we’re interested in.
\[\frac{1}{R} = \frac{1}{{80}} + \frac{1}{{105}} = \frac{{37}}{{1680}}\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}R = \frac{{1680}}{{37}} = 45.4054\,\Omega \]Next, we need to differentiate the equation given in the problem statement.
\[\begin{align*} - \frac{1}{{{R^2}}}R' & = - \frac{1}{{{{\left( {{R_{\,1}}} \right)}^2}}}{{R'}_{\,1}} - \frac{1}{{{{\left( {{R_{\,2}}} \right)}^2}}}{{R'}_{\,2}}\\ R' &= {R^2}\left( {\frac{1}{{{{\left( {{R_{\,1}}} \right)}^2}}}{{R'}_{\,1}} + \frac{1}{{{{\left( {{R_{\,2}}} \right)}^2}}}{{R'}_{\,2}}} \right)\end{align*}\]Finally, all we need to do is plug into this and do some quick computations.
\[R' = {\left( {45.4054} \right)^2}\left( {\frac{1}{{{{80}^2}}}\left( {0.4} \right) + \frac{1}{{{{105}^2}}}\left( { - 0.7} \right)} \right) = - 0.002045\]So, it looks like \(R\) is decreasing at a rate of 0.002045\(\Omega \)/min.
We’ve seen quite a few related rates problems in this section that cover a wide variety of possible problems. There are still many more different kinds of related rates problems out there in the world, but the ones that we’ve worked here should give you a pretty good idea on how to at least start most of the problems that you’re liable to run into.