Section 2.1 : Linear Differential Equations
The first special case of first order differential equations that we will look at is the linear first order differential equation. In this case, unlike most of the first order cases that we will look at, we can actually derive a formula for the general solution. The general solution is derived below. However, we would suggest that you do not memorize the formula itself. Instead of memorizing the formula you should memorize and understand the process that I'm going to use to derive the formula. Most problems are actually easier to work by using the process instead of using the formula.
So, let's see how to solve a linear first order differential equation. Remember as we go through this process that the goal is to arrive at a solution that is in the form \(y = y\left( t \right)\). It's sometimes easy to lose sight of the goal as we go through this process for the first time.
In order to solve a linear first order differential equation we MUST start with the differential equation in the form shown below. If the differential equation is not in this form then the process we’re going to use will not work.
\[\begin{equation}\frac{{dy}}{{dt}} + p\left( t \right)y = g\left( t \right) \label{eq:eq1} \end{equation}\]Where both \(p(t)\) and \(g(t)\) are continuous functions. Recall that a quick and dirty definition of a continuous function is that a function will be continuous provided you can draw the graph from left to right without ever picking up your pencil/pen. In other words, a function is continuous if there are no holes or breaks in it.
Now, we are going to assume that there is some magical function somewhere out there in the world, \(\mu \left( t \right)\), called an integrating factor. Do not, at this point, worry about what this function is or where it came from. We will figure out what \(\mu \left( t \right)\) is once we have the formula for the general solution in hand.
So, now that we have assumed the existence of \(\mu \left( t \right)\) multiply everything in \(\eqref{eq:eq1}\) by \(\mu \left( t \right)\). This will give.
\[\begin{equation}\mu \left( t \right)\frac{{dy}}{{dt}} + \mu \left( t \right)p\left( t \right)y = \mu \left( t \right)g\left( t \right) \label{eq:eq2} \end{equation}\]Now, this is where the magic of \(\mu \left( t \right)\) comes into play. We are going to assume that whatever \(\mu \left( t \right)\) is, it will satisfy the following.
\[\begin{equation}\mu \left( t \right)p\left( t \right) = \mu '\left( t \right) \label{eq:eq3} \end{equation}\]Again do not worry about how we can find a \(\mu \left( t \right)\) that will satisfy \(\eqref{eq:eq3}\). As we will see, provided \(p(t)\) is continuous we can find it. So substituting \(\eqref{eq:eq3}\) we now arrive at.
\[\begin{equation}\mu \left( t \right)\frac{{dy}}{{dt}} + \mu '\left( t \right)y = \mu \left( t \right)g\left( t \right) \label{eq:eq4} \end{equation}\]At this point we need to recognize that the left side of \(\eqref{eq:eq4}\) is nothing more than the following product rule.
\[\mu \left( t \right)\frac{{dy}}{{dt}} + \mu '\left( t \right)y = {\left( {\mu \left( t \right)y\left( t \right)} \right)^\prime }\]So we can replace the left side of \(\eqref{eq:eq4}\) with this product rule. Upon doing this \(\eqref{eq:eq4}\) becomes
\[\begin{equation}{\left( {\mu \left( t \right)y\left( t \right)} \right)^\prime } = \mu \left( t \right)g\left( t \right) \label{eq:eq5} \end{equation}\]Now, recall that we are after \(y(t)\). We can now do something about that. All we need to do is integrate both sides then use a little algebra and we'll have the solution. So, integrate both sides of \(\eqref{eq:eq5}\) to get.
\[\int{{{{\left( {\mu \left( t \right)y\left( t \right)} \right)}^\prime }\,dt}} = \int{{\mu \left( t \right)g\left( t \right)\,dt}}\] \[\begin{equation}\mu \left( t \right)y\left( t \right) + c = \int{{\mu \left( t \right)g\left( t \right)\,dt}} \label{eq:eq6} \end{equation}\]Note the constant of integration, \(c\), from the left side integration is included here. It is vitally important that this be included. If it is left out you will get the wrong answer every time.
The final step is then some algebra to solve for the solution, \(y(t)\).
\[\begin{align*}\mu \left( t \right)y\left( t \right) & = \int{{\mu \left( t \right)g\left( t \right)\,dt}} - c\\ y\left( t \right) & = \frac{{\int{{\mu \left( t \right)g\left( t \right)\,dt}} - c}}{{\mu \left( t \right)}}\end{align*}\]Now, from a notational standpoint we know that the constant of integration, \(c\), is an unknown constant and so to make our life easier we will absorb the minus sign in front of it into the constant and use a plus instead. This will NOT affect the final answer for the solution. So with this change we have.
\[\begin{equation}y\left( t \right) = \frac{{\int{{\mu \left( t \right)g\left( t \right)\,dt}} + c}}{{\mu \left( t \right)}} \label{eq:eq7} \end{equation}\]Again, changing the sign on the constant will not affect our answer. If you choose to keep the minus sign you will get the same value of \(c\) as we do except it will have the opposite sign. Upon plugging in \(c\) we will get exactly the same answer.
There is a lot of playing fast and loose with constants of integration in this section, so you will need to get used to it. When we do this we will always to try to make it very clear what is going on and try to justify why we did what we did.
So, now that we’ve got a general solution to \(\eqref{eq:eq1}\) we need to go back and determine just what this magical function \(\mu \left( t \right)\) is. This is actually an easier process than you might think. We’ll start with \(\eqref{eq:eq3}\).
\[\mu \left( t \right)p\left( t \right) = \mu '\left( t \right)\]Divide both sides by \(\mu \left( t \right)\),
\[\frac{{\mu '\left( t \right)}}{{\mu \left( t \right)}} = p\left( t \right)\]Now, hopefully you will recognize the left side of this from your Calculus I class as nothing more than the following derivative.
\[{\left( {\ln \mu \left( t \right)} \right)^\prime } = p\left( t \right)\]As with the process above all we need to do is integrate both sides to get.
\[\begin{align*}\ln \mu \left( t \right) + k &= \int{{p\left( t \right)\,dt}}\\ \ln \mu \left( t \right) & = \int{{p\left( t \right)\,dt}} + k\end{align*}\]You will notice that the constant of integration from the left side, \(k\), had been moved to the right side and had the minus sign absorbed into it again as we did earlier. Also note that we’re using \(k\) here because we’ve already used \(c\) and in a little bit we’ll have both of them in the same equation. So, to avoid confusion we used different letters to represent the fact that they will, in all probability, have different values.
Exponentiate both sides to get \(\mu \left( t \right)\) out of the natural logarithm.
\[\mu \left( t \right) = {{\bf{e}}^{\int{{p\left( t \right)\,dt}}\, + \,k}}\]Now, it’s time to play fast and loose with constants again. It is inconvenient to have the \(k\) in the exponent so we’re going to get it out of the exponent in the following way.
\[\begin{align*}\mu \left( t \right) & = {{\bf{e}}^{\int{{p\left( t \right)\,dt}}\, + \,k}}\\ & = {{\bf{e}}^k}{{\bf{e}}^{\int{{p\left( t \right)\,dt}}}}\hspace{0.25in}\hspace{0.25in}{\mbox{Recall }}{x^{a + b}} = {x^a}{x^b}!\end{align*}\]Now, let’s make use of the fact that \(k\) is an unknown constant. If \(k\) is an unknown constant then so is \({{\bf{e}}^k}\) so we might as well just rename it \(k\) and make our life easier. This will give us the following.
\[\begin{equation}\mu \left( t \right) = k\,{{\bf{e}}^{\int{{p\left( t \right)\,dt}}}}\label{eq:eq8}\end{equation}\]So, we now have a formula for the general solution, \(\eqref{eq:eq7}\), and a formula for the integrating factor, \(\eqref{eq:eq8}\). We do have a problem however. We’ve got two unknown constants and the more unknown constants we have the more trouble we’ll have later on. Therefore, it would be nice if we could find a way to eliminate one of them (we’ll not be able to eliminate both….).
This is actually quite easy to do. First, substitute \(\eqref{eq:eq8}\) into \(\eqref{eq:eq7}\) and rearrange the constants.
\[\begin{align*}y\left( t \right) & = \frac{{\int{{k\,{{\bf{e}}^{\int{{p\left( t \right)\,dt}}}}g\left( t \right)\,dt}} + c}}{{k\,{{\bf{e}}^{\int{{p\left( t \right)\,dt}}}}}}\\ & = \frac{{k\int{{\,{{\bf{e}}^{\int{{p\left( t \right)\,dt}}}}g\left( t \right)\,dt}} + c}}{{k\,{{\bf{e}}^{\int{{p\left( t \right)\,dt}}}}}}\\ & = \frac{{\int{{\,{{\bf{e}}^{\int{{p\left( t \right)\,dt}}}}g\left( t \right)\,dt}} + \frac{c}{k}}}{{\,{{\bf{e}}^{\int{{p\left( t \right)\,dt}}}}}}\end{align*}\]So, \(\eqref{eq:eq7}\) can be written in such a way that the only place the two unknown constants show up is a ratio of the two. Then since both \(c\) and \(k\) are unknown constants so is the ratio of the two constants. Therefore we’ll just call the ratio \(c\) and then drop \(k\) out of \(\eqref{eq:eq8}\) since it will just get absorbed into \(c\) eventually.
The solution to a linear first order differential equation is then
\[\begin{equation}y\left( t \right) = \frac{{\int{{\mu \left( t \right)g\left( t \right)\,dt}} + c}}{{\mu \left( t \right)}}\label{eq:eq9}\end{equation}\]where,
\[\begin{equation}\mu \left( t \right) = \,{{\bf{e}}^{\int{{p\left( t \right)\,dt}}}}\label{eq:eq10}\end{equation}\]Now, the reality is that \(\eqref{eq:eq9}\) is not as useful as it may seem. It is often easier to just run through the process that got us to \(\eqref{eq:eq9}\) rather than using the formula. We will not use this formula in any of our examples. We will need to use \(\eqref{eq:eq10}\) regularly, as that formula is easier to use than the process to derive it.
Solution Process
The solution process for a first order linear differential equation is as follows.
- Put the differential equation in the correct initial form, \(\eqref{eq:eq1}\).
- Find the integrating factor, \(\mu \left( t \right)\), using \(\eqref{eq:eq10}\).
- Multiply everything in the differential equation by \(\mu \left( t \right)\) and verify that the left side becomes the product rule \(\left( {\mu \left( t \right)y\left( t \right)} \right)'\) and write it as such.
- Integrate both sides, make sure you properly deal with the constant of integration.
- Solve for the solution \(y(t)\).
Let’s work a couple of examples. Let’s start by solving the differential equation that we derived back in the Direction Field section.
First, we need to get the differential equation in the correct form.
\[\frac{{dv}}{{dt}} + 0.196v = 9.8\]From this we can see that \(p(t)=0.196\) and so \(\mu \left( t \right)\) is then.
\[\mu \left( t \right) = {{\bf{e}}^{\int{{0.196dt}}}} = {{\bf{e}}^{0.196t}}\]Note that officially there should be a constant of integration in the exponent from the integration. However, we can drop that for exactly the same reason that we dropped the \(k\) from \(\eqref{eq:eq8}\).
Now multiply all the terms in the differential equation by the integrating factor and do some simplification.
\[\begin{align*}{{\bf{e}}^{0.196t}}\frac{{dv}}{{dt}} + 0.196{{\bf{e}}^{0.196t}}v & = 9.8{{\bf{e}}^{0.196t}}\\ {\left( {{{\bf{e}}^{0.196t}}v} \right)^\prime } & = 9.8{{\bf{e}}^{0.196t}}\end{align*}\]Integrate both sides and don't forget the constants of integration that will arise from both integrals.
\[\begin{align*}\int{{{{\left( {{{\bf{e}}^{0.196t}}v} \right)}^\prime }\,dt}} & = \int{{9.8{{\bf{e}}^{0.196t}}\,dt}}\\ {{\bf{e}}^{0.196t}}v + k & = 50{{\bf{e}}^{0.196t}} + c\end{align*}\]Okay. It’s time to play with constants again. We can subtract \(k\) from both sides to get.
\[{{\bf{e}}^{0.196t}}v = 50{{\bf{e}}^{0.196t}} + c - k\]Both \(c\) and \(k\) are unknown constants and so the difference is also an unknown constant. We will therefore write the difference as \(c\). So, we now have
\[{{\bf{e}}^{0.196t}}v = 50{{\bf{e}}^{0.196t}} + c\]From this point on we will only put one constant of integration down when we integrate both sides knowing that if we had written down one for each integral, as we should, the two would just end up getting absorbed into each other.
The final step in the solution process is then to divide both sides by \({{\bf{e}}^{0.196t}}\) or to multiply both sides by \({{\bf{e}}^{ - 0.196t}}\). Either will work, but we usually prefer the multiplication route. Doing this gives the general solution to the differential equation.
\[v\left( t \right) = 50 + c{{\bf{e}}^{ - 0.196t}}\]From the solution to this example we can now see why the constant of integration is so important in this process. Without it, in this case, we would get a single, constant solution, \(v(t)=50\). With the constant of integration we get infinitely many solutions, one for each value of \(c\).
Back in the direction field section where we first derived the differential equation used in the last example we used the direction field to help us sketch some solutions. Let's see if we got them correct. To sketch some solutions all we need to do is to pick different values of \(c\) to get a solution. Several of these are shown in the graph below.
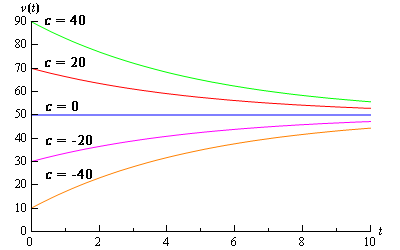
So, it looks like we did pretty good sketching the graphs back in the direction field section.
Now, recall from the Definitions section that the Initial Condition(s) will allow us to zero in on a particular solution. Solutions to first order differential equations (not just linear as we will see) will have a single unknown constant in them and so we will need exactly one initial condition to find the value of that constant and hence find the solution that we were after. The initial condition for first order differential equations will be of the form
\[y\left( {{t_0}} \right) = {y_0}\]Recall as well that a differential equation along with a sufficient number of initial conditions is called an Initial Value Problem (IVP).
To find the solution to an IVP we must first find the general solution to the differential equation and then use the initial condition to identify the exact solution that we are after. So, since this is the same differential equation as we looked at in Example 1, we already have its general solution.
\[v = 50 + c{{\bf{e}}^{ - 0.196t}}\]Now, to find the solution we are after we need to identify the value of \(c\) that will give us the solution we are after. To do this we simply plug in the initial condition which will give us an equation we can solve for \(c\). So, let's do this
\[48 = v\left( 0 \right) = 50 + c\hspace{0.25in} \Rightarrow \hspace{0.25in}c = - 2\]So, the actual solution to the IVP is.
\[v = 50 - 2{{\bf{e}}^{ - 0.196t}}\]A graph of this solution can be seen in the figure above.
Let’s do a couple of examples that are a little more involved.
Rewrite the differential equation to get the coefficient of the derivative to be one.
\[\begin{align*}y' + \frac{{\sin \left( x \right)}}{{\cos \left( x \right)}}y & = 2{\cos ^2}\left( x \right)\sin \left( x \right) - \frac{1}{{\cos \left( x \right)}}\\ y' + \tan \left( x \right)y &= 2{\cos ^2}\left( x \right)\sin \left( x \right) - \sec \left( x \right)\end{align*}\]Now find the integrating factor.
\[\mu \left( x \right) = {{\bf{e}}^{\int{{\tan \left( x \right)\,dx}}}} = {{\bf{e}}^{\ln \left| {\sec \left( x \right)} \right|}} = {{\bf{e}}^{\ln \,\,\sec \left( x \right)}} = \sec \left( x \right)\]Can you do the integral? If not rewrite tangent back into sines and cosines and then use a simple substitution. Note that we could drop the absolute value bars on the secant because of the limits on \(x\). In fact, this is the reason for the limits on \(x\). Note as well that there are two forms of the answer to this integral. They are equivalent as shown below. Which you use is really a matter of preference.
\[\int{{\tan \left( x \right)\,dx}} = - \ln \left| {\cos \left( x \right)} \right| = \ln {\left| {\cos \left( x \right)} \right|^{ - 1}} = \ln \left| {\sec \left( x \right)} \right|\]Also note that we made use of the following fact.
\[\begin{equation}{{\bf{e}}^{\ln f\left( x \right)}} = f\left( x \right) \label{eq:eq11}\end{equation}\]This is an important fact that you should always remember for these problems. We will want to simplify the integrating factor as much as possible in all cases and this fact will help with that simplification.
Now back to the example. Multiply the integrating factor through the differential equation and verify the left side is a product rule. Note as well that we multiply the integrating factor through the rewritten differential equation and NOT the original differential equation. Make sure that you do this. If you multiply the integrating factor through the original differential equation you will get the wrong solution!
\[\begin{align*}\sec \left( x \right)y' + \sec \left( x \right)\tan \left( x \right)y & = 2\sec \left( x \right){\cos ^2}\left( x \right)\sin \left( x \right) - {\sec ^2}\left( x \right)\\ {\left( {\sec \left( x \right)y} \right)^\prime } & = 2\cos \left( x \right)\sin \left( x \right) - {\sec ^2}\left( x \right)\end{align*}\]Integrate both sides.
\[\begin{align*}\int{{{{\left( {\sec \left( x \right)y\left( x \right)} \right)}^\prime }\,dx}} & = \int{{2\cos \left( x \right)\sin \left( x \right) - {{\sec }^2}\left( x \right)\,dx}}\\ \sec \left( x \right)y\left( x \right) & = \int{{\sin \left( {2x} \right) - {{\sec }^2}\left( x \right)\,dx}}\\ \sec \left( x \right)y\left( x \right) & = - \frac{1}{2}\cos \left( {2x} \right) - \tan \left( x \right) + c\end{align*}\]Note the use of the trig formula \(\sin \left( {2\theta } \right) = 2\sin \theta \cos \theta \) that made the integral easier. Next, solve for the solution.
\[\begin{align*}y\left( x \right) & = - \frac{1}{2}\cos \left( x \right)\cos \left( {2x} \right) - \cos \left( x \right)\tan \left( x \right) + c\cos \left( x \right)\\ & = - \frac{1}{2}\cos \left( x \right)\cos \left( {2x} \right) - \sin \left( x \right) + c\cos \left( x \right)\end{align*}\]Finally, apply the initial condition to find the value of \(c\).
\[\begin{align*}3\sqrt 2 = y\left( {\frac{\pi }{4}} \right) & = - \frac{1}{2}\cos \left( {\frac{\pi }{4}} \right)\cos \left( {\frac{\pi }{2}} \right) - \sin \left( {\frac{\pi }{4}} \right) + c\cos \left( {\frac{\pi }{4}} \right)\\ 3\sqrt 2 & = - \frac{{\sqrt 2 }}{2} + c\frac{{\sqrt 2 }}{2}\\ c & = 7\end{align*}\]The solution is then.
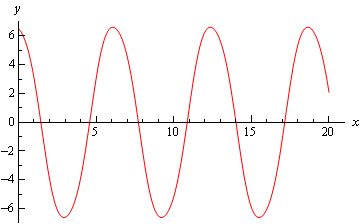
\[y\left( x \right) = - \frac{1}{2}\cos \left( x \right)\cos \left( {2x} \right) - \sin \left( x \right) + 7\cos \left( x \right)\]Below is a plot of the solution.
First, divide through by the t to get the differential equation into the correct form.
\[y' + \frac{2}{t}y = t - 1 + \frac{1}{t}\]Now let’s get the integrating factor, \(\mu \left( t \right)\).
\[\mu \left( t \right) = {{\bf{e}}^{\int{{\frac{2}{t}dt}}}} = {{\bf{e}}^{2\ln \left| {\,t} \right|}}\]Now, we need to simplify \(\mu \left( t \right)\). However, we can’t use \(\eqref{eq:eq11}\) yet as that requires a coefficient of one in front of the logarithm. So, recall that
\[\ln {x^r} = r\ln x\]and rewrite the integrating factor in a form that will allow us to simplify it.
\[\mu \left( t \right) = {{\bf{e}}^{2\ln \left| {\,t} \right|}} = {{\bf{e}}^{\ln {{\left| {\,t} \right|}^2}}} = {\left| t \right|^2} = {t^2}\]We were able to drop the absolute value bars here because we were squaring the \(t\), but often they can’t be dropped so be careful with them and don’t drop them unless you know that you can. Often the absolute value bars must remain.
Now, multiply the rewritten differential equation (remember we can’t use the original differential equation here…) by the integrating factor.
\[{\left( {{t^2}y} \right)^\prime } = {t^3} - {t^2} + t\]Integrate both sides and solve for the solution.
\[\begin{align*}{t^2}y & = \int{{{t^3} - {t^2} + t\,dt}}\\ & = \frac{1}{4}{t^4} - \frac{1}{3}{t^3} + \frac{1}{2}{t^2} + c\\ y\left( t \right) & = \frac{1}{4}{t^2} - \frac{1}{3}t + \frac{1}{2} + \frac{c}{{{t^2}}}\end{align*}\]Finally, apply the initial condition to get the value of \(c\).
\[\frac{1}{2} = y\left( 1 \right) = \frac{1}{4} - \frac{1}{3} + \frac{1}{2} + c\hspace{0.25in} \Rightarrow \hspace{0.25in}\,\,\,c = \frac{1}{{12}}\]The solution is then,
\[y\left( t \right) = \frac{1}{4}{t^2} - \frac{1}{3}t + \frac{1}{2} + \frac{1}{{12{t^2}}}\]Here is a plot of the solution.

First, divide through by \(t\) to get the differential equation in the correct form.
\[y' - \frac{2}{t}y = {t^4}\sin \left( {2t} \right) - {t^2} + 4{t^3}\]Now that we have done this we can find the integrating factor, \(\mu \left( t \right)\).
\[\mu \left( t \right) = {{\bf{e}}^{\int{{ - \frac{2}{t}dt}}}} = {{\bf{e}}^{ - 2\ln \left| {\,t} \right|}}\]Do not forget that the “-” is part of \(p(t)\). Forgetting this minus sign can take a problem that is very easy to do and turn it into a very difficult, if not impossible problem so be careful!
Now, we just need to simplify this as we did in the previous example.
\[\mu \left( t \right) = {{\bf{e}}^{ - 2\ln \left| {\,t} \right|}} = {{\bf{e}}^{\ln {{\left| {\,t} \right|}^{\, - \,2}}}} = {\left| t \right|^{ - 2}} = {t^{ - 2}}\]Again, we can drop the absolute value bars since we are squaring the term.
Now multiply the differential equation by the integrating factor (again, make sure it’s the rewritten one and not the original differential equation).
\[{\left( {{t^{ - 2}}y} \right)^\prime } = {t^2}\sin \left( {2t} \right) - 1 + 4t\]Integrate both sides and solve for the solution.
\[\begin{align*}{t^{ - 2}}y\left( t \right) & = \int{{{t^2}\sin \left( {2t} \right)\,dt}} + \int{{ - 1 + 4t\,dt}}\\ {t^{ - 2}}y\left( t \right) & = - \frac{1}{2}{t^2}\cos \left( {2t} \right) + \frac{1}{2}t\sin \left( {2t} \right) + \frac{1}{4}\cos \left( {2t} \right) - t + 2{t^2} + c\\ y\left( t \right) & = - \frac{1}{2}{t^4}\cos \left( {2t} \right) + \frac{1}{2}{t^3}\sin \left( {2t} \right) + \frac{1}{4}{t^2}\cos \left( {2t} \right) - {t^3} + 2{t^4} + c{t^2}\end{align*}\]Apply the initial condition to find the value of \(c\).
\[\begin{align*}\frac{3}{2}{\pi ^4} = y\left( \pi \right) & = - \frac{1}{2}{\pi ^4} + \frac{1}{4}{\pi ^2} - {\pi ^3} + 2{\pi ^4} + c{\pi ^2} = \frac{3}{2}{\pi ^4} - {\pi ^3} + \frac{1}{4}{\pi ^2} + c{\pi ^2}\\ {\pi ^3} - \frac{1}{4}{\pi ^2} & = c{\pi ^2}\\ c & = \pi - \frac{1}{4}\end{align*}\]The solution is then
\[y\left( t \right) = - \frac{1}{2}{t^4}\cos \left( {2t} \right) + \frac{1}{2}{t^3}\sin \left( {2t} \right) + \frac{1}{4}{t^2}\cos \left( {2t} \right) - {t^3} + 2{t^4} + \left( {\pi - \frac{1}{4}} \right){t^2}\]Below is a plot of the solution.

Let’s work one final example that looks more at interpreting a solution rather than finding a solution.
First, divide through by a 2 to get the differential equation in the correct form.
\[y' - \frac{1}{2}y = 2\sin \left( {3t} \right)\]Now find \(\mu \left( t \right)\).
\[\mu \left( t \right) = {{\bf{e}}^{\int{{ - \frac{1}{2}dt}}}} = {{\bf{e}}^{ - \frac{t}{2}}}\]Multiply \(\mu \left( t \right)\)through the differential equation and rewrite the left side as a product rule.
\[{\left( {{{\bf{e}}^{ - \frac{t}{2}}}y} \right)^\prime } = 2{{\bf{e}}^{ - \frac{t}{2}}}\sin \left( {3t} \right)\]Integrate both sides (the right side requires integration by parts – you can do that right?) and solve for the solution.
\[\begin{align*}{{\bf{e}}^{ - \frac{t}{2}}}y & = \int{{2{{\bf{e}}^{ - \frac{t}{2}}}\sin \left( {3t} \right)\,dt}} + c\\ {{\bf{e}}^{ - \frac{t}{2}}}y & = - \frac{{24}}{{37}}{{\bf{e}}^{ - \frac{t}{2}}}\cos \left( {3t} \right)\, - \frac{4}{{37}}{{\bf{e}}^{ - \frac{t}{2}}}\sin \left( {3t} \right)\, + c\\ y\left( t \right) & = - \frac{{24}}{{37}}\cos \left( {3t} \right)\, - \frac{4}{{37}}\sin \left( {3t} \right)\, + c{{\bf{e}}^{\frac{t}{2}}}\end{align*}\]Apply the initial condition to find the value of \(c\) and note that it will contain \(y_{0}\) as we don’t have a value for that.
\[{y_0} = y\left( 0 \right) = - \frac{{24}}{{37}} + c\hspace{0.25in}\,\,\,\, \Rightarrow \hspace{0.25in}\,\,c = {y_0} + \frac{{24}}{{37}}\]So, the solution is
\[y\left( t \right) = - \frac{{24}}{{37}}\cos \left( {3t} \right)\, - \frac{4}{{37}}\sin \left( {3t} \right)\, + \left( {{y_0} + \frac{{24}}{{37}}} \right){{\bf{e}}^{\frac{t}{2}}}\]Now that we have the solution, let’s look at the long term behavior (i.e. \(t \to \infty \)) of the solution. The first two terms of the solution will remain finite for all values of \(t\). It is the last term that will determine the behavior of the solution. The exponential will always go to infinity as \(t \to \infty \), however depending on the sign of the coefficient \(c\) (yes we’ve already found it, but for ease of this discussion we’ll continue to call it \(c\)). The following table gives the long term behavior of the solution for all values of \(c\).
| Range of \(c\) | Behavior of solution as\(t \to \infty \) |
|---|---|
| \(c\) < 0 | \(y\left( t \right) \to - \infty \) |
| \(c\) = 0 | \(y\left( t \right)\) remains finite |
| \(c\) > 0 | \(y\left( t \right) \to \infty \) |
This behavior can also be seen in the following graph of several of the solutions.

Now, because we know how \(c\) relates to \(y_{0}\) we can relate the behavior of the solution to \(y_{0}\). The following table give the behavior of the solution in terms of \(y_{0}\) instead of \(c\).
| Range of \(y_{0}\) | Behavior of solution as\(t \to \infty \) |
|---|---|
| \({y_0} < - \frac{{24}}{{37}}\) | \(y\left( t \right) \to - \infty \) |
| \({y_0} = - \frac{{24}}{{37}}\) | \(y\left( t \right)\) remains finite |
| \({y_0} > - \frac{{24}}{{37}}\) | \(y\left( t \right) \to \infty \) |
Note that for \({y_0} = - \frac{{24}}{{37}}\) the solution will remain finite. That will not always happen.
Investigating the long term behavior of solutions is sometimes more important than the solution itself. Suppose that the solution above gave the temperature in a bar of metal. In this case we would want the solution(s) that remains finite in the long term. With this investigation we would now have the value of the initial condition that will give us that solution and more importantly values of the initial condition that we would need to avoid so that we didn’t melt the bar.