Section 12.3 : Equations of Planes
In the first section of this chapter we saw a couple of equations of planes. However, none of those equations had three variables in them and were really extensions of graphs that we could look at in two dimensions. We would like a more general equation for planes.
So, let’s start by assuming that we know a point that is on the plane, \({P_0} = \left( {{x_0},{y_0},{z_0}} \right)\). Let’s also suppose that we have a vector that is orthogonal (perpendicular) to the plane, \(\vec n = \left\langle {a,b,c} \right\rangle \). This vector is called the normal vector. Now, assume that \(P = \left( {x,y,z} \right)\) is any point in the plane. Finally, since we are going to be working with vectors initially we’ll let \(\overrightarrow {{r_0}} \) and \(\vec r\) be the position vectors for P0 and \(P\) respectively.
Here is a sketch of all these vectors.
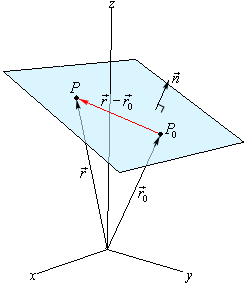
Notice that we added in the vector \(\vec r - \overrightarrow {{r_0}} \) which will lie completely in the plane. Also notice that we put the normal vector on the plane, but there is actually no reason to expect this to be the case. We put it here to illustrate the point. It is completely possible that the normal vector does not touch the plane in any way.
Now, because \(\vec n\) is orthogonal to the plane, it’s also orthogonal to any vector that lies in the plane. In particular it’s orthogonal to \(\vec r - \overrightarrow {{r_0}} \). Recall from the Dot Product section that two orthogonal vectors will have a dot product of zero. In other words,
\[\vec n\centerdot \left( {\vec r - \overrightarrow {{r_0}} } \right) = 0\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}\vec n\centerdot \vec r = \vec n\centerdot \overrightarrow {{r_0}} \]This is called the vector equation of the plane.
A slightly more useful form of the equations is as follows. Start with the first form of the vector equation and write down a vector for the difference.
\[\begin{align*}\left\langle {a,b,c} \right\rangle \centerdot \left( {\left\langle {x,y,z} \right\rangle - \left\langle {{x_0},{y_0},{z_0}} \right\rangle } \right)& = 0\\ \left\langle {a,b,c} \right\rangle \centerdot \left\langle {x - {x_0},y - {y_0},z - {z_0}} \right\rangle & = 0\end{align*}\]Now, actually compute the dot product to get,
This is called the scalar equation of plane. Often this will be written as,
\[ax + by + cz = d\]where \(d = a{x_0} + b{y_0} + c{z_0}\).
This second form is often how we are given equations of planes. Notice that if we are given the equation of a plane in this form we can quickly get a normal vector for the plane. A normal vector is,
\[\vec n = \left\langle {a,b,c} \right\rangle \]Let’s work a couple of examples.
In order to write down the equation of plane we need a point (we’ve got three so we’re cool there) and a normal vector. We need to find a normal vector. Recall however, that we saw how to do this in the Cross Product section.
We can form the following two vectors from the given points.
\[\overrightarrow {PQ} = \left\langle {2,3,4} \right\rangle \hspace{0.25in}\hspace{0.25in}\overrightarrow {PR} = \left\langle { - 1,1,2} \right\rangle \]These two vectors will lie completely in the plane since we formed them from points that were in the plane. Notice as well that there are many possible vectors to use here, we just chose two of the possibilities.
Now, we know that the cross product of two vectors will be orthogonal to both of these vectors. Since both of these are in the plane any vector that is orthogonal to both of these will also be orthogonal to the plane. Therefore, we can use the cross product as the normal vector.
\[\vec n = \overrightarrow {PQ} \times \overrightarrow {PR} = \left| {\begin{array}{*{20}{c}}{\vec i}&{\vec j}&{\vec k}\\2&3&4\\{ - 1}&1&2\end{array}} \right|\,\,\,\,\begin{array}{*{20}{c}}{\vec i}&{\vec j}\\2&3\\{ - 1}&1\end{array} = 2\vec i - 8\vec j + 5\vec k\]The equation of the plane is then,
\[\begin{align*}2\left( {x - 1} \right) - 8\left( {y + 2} \right) + 5\left( {z - 0} \right) & = 0\\ 2x - 8y + 5z & = 18\end{align*}\]We used \(P\) for the point but could have used any of the three points.
This is not as difficult a problem as it may at first appear to be. We can pick off a vector that is normal to the plane. This is \(\vec n = \left\langle { - 1,0,2} \right\rangle \). We can also get a vector that is parallel to the line. This is \(v = \left\langle {0, - 1,4} \right\rangle \).
Now, if these two vectors are parallel then the line and the plane will be orthogonal. If you think about it this makes some sense. If \(\vec n\) and \(\vec v\) are parallel, then \(\vec v\) is orthogonal to the plane, but \(\vec v\) is also parallel to the line. So, if the two vectors are parallel the line and plane will be orthogonal.
Let’s check this.
\[\vec n \times \vec v = \left| {\begin{array}{*{20}{c}}{\vec i}&{\vec j}&{\vec k}\\{ - 1}&0&2\\0&{ - 1}&4\end{array}} \right|\,\,\,\,\begin{array}{*{20}{c}}{\vec i}&{\vec j}\\{ - 1}&0\\0&{ - 1}\end{array} = 2\vec i + 4\vec j + \vec k \ne \vec 0\]So, the vectors aren’t parallel and so the plane and the line are not orthogonal.
Now, let’s check to see if the plane and line are parallel. If the line is parallel to the plane then any vector parallel to the line will be orthogonal to the normal vector of the plane. In other words, if \(\vec n\) and \(\vec v\) are orthogonal then the line and the plane will be parallel.
Let’s check this.
\[\vec n\centerdot \vec v = 0 + 0 + 8 = 8 \ne 0\]The two vectors aren’t orthogonal and so the line and plane aren’t parallel.
So, the line and the plane are neither orthogonal nor parallel.