Section 9.6 : Polar Coordinates
Up to this point we’ve dealt exclusively with the Cartesian (or Rectangular, or x-y) coordinate system. However, as we will see, this is not always the easiest coordinate system to work in. So, in this section we will start looking at the polar coordinate system.
Coordinate systems are really nothing more than a way to define a point in space. For instance in the Cartesian coordinate system at point is given the coordinates \(\left( {x,y} \right)\) and we use this to define the point by starting at the origin and then moving \(x\) units horizontally followed by \(y\) units vertically. This is shown in the sketch below.
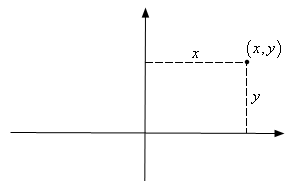
This is not, however, the only way to define a point in two dimensional space. Instead of moving vertically and horizontally from the origin to get to the point we could instead go straight out of the origin until we hit the point and then determine the angle this line makes with the positive \(x\)-axis. We could then use the distance of the point from the origin and the amount we needed to rotate from the positive \(x\)-axis as the coordinates of the point. This is shown in the sketch below.
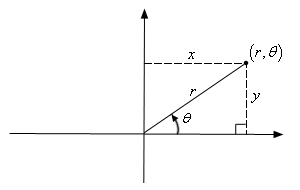
Coordinates in this form are called polar coordinates.
The above discussion may lead one to think that \(r\) must be a positive number. However, we also allow \(r\) to be negative. Below is a sketch of the two points \(\left( {2,\frac{\pi }{6}} \right)\) and \(\left( { - 2,\frac{\pi }{6}} \right)\).
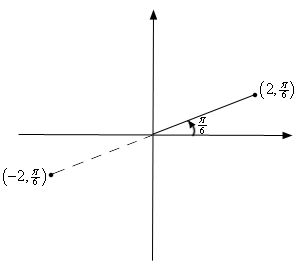
From this sketch we can see that if \(r\) is positive the point will be in the same quadrant as \(\theta \). On the other hand if \(r\) is negative the point will end up in the quadrant exactly opposite \(\theta \). Notice as well that the coordinates \(\left( { - 2,\frac{\pi }{6}} \right)\) describe the same point as the coordinates \(\left( {2,\frac{{7\pi }}{6}} \right)\) do. The coordinates \(\left( {2,\frac{{7\pi }}{6}} \right)\) tells us to rotate an angle of \(\frac{{7\pi }}{6}\) from the positive \(x\)-axis, this would put us on the dashed line in the sketch above, and then move out a distance of 2.
This leads to an important difference between Cartesian coordinates and polar coordinates. In Cartesian coordinates there is exactly one set of coordinates for any given point. With polar coordinates this isn’t true. In polar coordinates there is literally an infinite number of coordinates for a given point. For instance, the following four points are all coordinates for the same point.
\[\left( {5,\frac{\pi }{3}} \right) = \left( {5, - \frac{{5\pi }}{3}} \right) = \left( { - 5,\frac{{4\pi }}{3}} \right) = \left( { - 5, - \frac{{2\pi }}{3}} \right)\]Here is a sketch of the angles used in these four sets of coordinates.
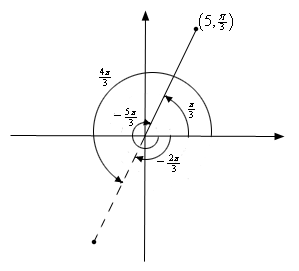
In the second coordinate pair we rotated in a clock-wise direction to get to the point. We shouldn’t forget about rotating in the clock-wise direction. Sometimes it’s what we have to do.
The last two coordinate pairs use the fact that if we end up in the opposite quadrant from the point we can use a negative \(r\) to get back to the point and of course there is both a counter clock-wise and a clock-wise rotation to get to the angle.
These four points only represent the coordinates of the point without rotating around the system more than once. If we allow the angle to make as many complete rotations about the axis system as we want then there are an infinite number of coordinates for the same point. In fact, the point \(\left( {r,\theta } \right)\) can be represented by any of the following coordinate pairs.
\[\left( {r,\theta + 2\pi n} \right)\hspace{0.25in}\hspace{0.25in}\left( { - r,\theta + \left( {2n + 1} \right)\pi } \right),\hspace{0.25in}\,\,\,\,\,{\mbox{where }}n{\mbox{ is any integer}}{\mbox{.}}\]Next, we should talk about the origin of the coordinate system. In polar coordinates the origin is often called the pole. Because we aren’t actually moving away from the origin/pole we know that \(r = 0\). However, we can still rotate around the system by any angle we want and so the coordinates of the origin/pole are \(\left( {0,\theta } \right)\).
Now that we’ve got a grasp on polar coordinates we need to think about converting between the two coordinate systems. Well start out with the following sketch reminding us how both coordinate systems work.

Note that we’ve got a right triangle above and with that we can get the following equations that will convert polar coordinates into Cartesian coordinates.
Polar to Cartesian Conversion Formulas
Converting from Cartesian is almost as easy. Let’s first notice the following.
\[\begin{align*}{x^2} + {y^2} & = {\left( {r\cos \theta } \right)^2} + {\left( {r\sin \theta } \right)^2}\\ & = {r^2}{\cos ^2}\theta + {r^2}{\sin ^2}\theta \\ & = {r^2}\left( {{{\cos }^2}\theta + {{\sin }^2}\theta } \right) = {r^2}\end{align*}\]This is a very useful formula that we should remember, however we are after an equation for \(r\) so let’s take the square root of both sides. This gives,
\[r = \sqrt {{x^2} + {y^2}} \]Note that technically we should have a plus or minus in front of the root since we know that \(r\) can be either positive or negative. We will run with the convention of positive \(r\) here.
Getting an equation for \(\theta \) is almost as simple. We’ll start with,
\[\frac{y}{x} = \frac{{r\sin \theta }}{{r\cos \theta }} = \tan \theta \]Taking the inverse tangent of both sides gives,
\[\theta = {\tan ^{ - 1}}\left( {\frac{y}{x}} \right)\]We will need to be careful with this because inverse tangents only return values in the range \( - \frac{\pi }{2} < \theta < \frac{\pi }{2}\). Recall that there is a second possible angle and that the second angle is given by \(\theta + \pi \).
Summarizing then gives the following formulas for converting from Cartesian coordinates to polar coordinates.
Cartesian to Polar Conversion Formulas
Let’s work a quick example.
- Convert \(\left( { - 4,\frac{{2\pi }}{3}} \right)\) into Cartesian coordinates.
- Convert \(\left( { - 1,-1} \right)\) into polar coordinates.
This conversion is easy enough. All we need to do is plug the points into the formulas.
\[\begin{align*}x & = - 4\cos \left( {\frac{{2\pi }}{3}} \right) = - 4\left( { - \frac{1}{2}} \right) = 2\\ y & = - 4\sin \left( {\frac{{2\pi }}{3}} \right) = - 4\left( {\frac{{\sqrt 3 }}{2}} \right) = - 2\sqrt 3 \end{align*}\]So, in Cartesian coordinates this point is \(\left( {2, - 2\sqrt 3 } \right)\).
b Convert \(\left( { - 1,-1} \right)\) into polar coordinates. Show Solution
Let’s first get \(r\).
\[r = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 1} \right)}^2}} = \sqrt 2 \]Now, let’s get \(\theta \).
\[\theta = {\tan ^{ - 1}}\left( {\frac{{ - 1}}{{ - 1}}} \right) = {\tan ^{ - 1}}\left( 1 \right) = \frac{\pi }{4}\]This is not the correct angle however. This value of \(\theta \) is in the first quadrant and the point we’ve been given is in the third quadrant. As noted above we can get the correct angle by adding \(\pi\) onto this. Therefore, the actual angle is,
\[\theta = \frac{\pi }{4} + \pi = \frac{{5\pi }}{4}\]So, in polar coordinates the point is \(\left( {\sqrt 2 ,\frac{{5\pi }}{4}} \right)\). Note as well that we could have used the first \(\theta \) that we got by using a negative \(r\). In this case the point could also be written in polar coordinates as \(\left( { - \sqrt 2 ,\frac{\pi }{4}} \right)\).
We can also use the above formulas to convert equations from one coordinate system to the other.
- Convert \(2x - 5{x^3} = 1 + xy\) into polar coordinates.
- Convert \(r = - 8\cos \theta \) into Cartesian coordinates.
In this case there really isn’t much to do other than plugging in the formulas for \(x\) and \(y\) (i.e. the Cartesian coordinates) in terms of \(r\) and \(\theta \) (i.e. the polar coordinates).
\[\begin{align*}2\left( {r\cos \theta } \right) - 5{\left( {r\cos \theta } \right)^3} & = 1 + \left( {r\cos \theta } \right)\left( {r\sin \theta } \right)\\ 2r\cos \theta - 5{r^3}{\cos ^3}\theta & = 1 + {r^2}\cos \theta \sin \theta \end{align*}\]b Convert \(r = - 8\cos \theta \) into Cartesian coordinates. Show Solution
This one is a little trickier, but not by much. First notice that we could substitute straight for the \(r\). However, there is no straight substitution for the cosine that will give us only Cartesian coordinates. If we had an \(r\) on the right along with the cosine then we could do a direct substitution. So, if an \(r\) on the right side would be convenient let’s put one there, just don’t forget to put one on the left side as well.
\[{r^2} = - 8r\cos \theta \]We can now make some substitutions that will convert this into Cartesian coordinates.
\[{x^2} + {y^2} = - 8x\]Before moving on to the next subject let’s do a little more work on the second part of the previous example.
The equation given in the second part is actually a fairly well known graph; it just isn’t in a form that most people will quickly recognize. To identify it let’s take the Cartesian coordinate equation and do a little rearranging.
\[{x^2} + 8x + {y^2} = 0\]Now, complete the square on the \(x\) portion of the equation.
\[\begin{align*}{x^2} + 8x + 16 + {y^2} & = 16\\ {\left( {x + 4} \right)^2} + {y^2} & = 16\end{align*}\]So, this was a circle of radius 4 and center \(\left( { - 4,0} \right)\).
This leads us into the final topic of this section.
Common Polar Coordinate Graphs
Let’s identify a few of the more common graphs in polar coordinates. We’ll also take a look at a couple of special polar graphs.
Lines
Some lines have fairly simple equations in polar coordinates.
- \(\theta = \beta \).
We can see that this is a line by converting to Cartesian coordinates as follows \[\begin{align*}\theta & = \beta \\ {\tan ^{ - 1}}\left( {\frac{y}{x}} \right) & = \beta \\ \frac{y}{x} & = \tan \beta \\ y & = \left( {\tan \beta } \right)x\end{align*}\]This is a line that goes through the origin and makes an angle of \(\beta \) with the positive \(x\)-axis. Or, in other words it is a line through the origin with slope of \(\tan \beta \).
- \(r\cos \theta = a\)
This is easy enough to convert to Cartesian coordinates to \(x = a\). So, this is a vertical line. - \(r\sin \theta = b\)
Likewise, this converts to \(y = b\) and so is a horizontal line.
There really isn’t too much to this one other than doing the graph so here it is.

Circles
Let’s take a look at the equations of circles in polar coordinates.
- \(r = a\).
This equation is saying that no matter what angle we’ve got the distance from the origin must be \(a\). If you think about it that is exactly the definition of a circle of radius \(a\) centered at the origin.So, this is a circle of radius \(a\) centered at the origin. This is also one of the reasons why we might want to work in polar coordinates. The equation of a circle centered at the origin has a very nice equation, unlike the corresponding equation in Cartesian coordinates.
- \(r = 2a\cos \theta \).
We looked at a specific example of one of these when we were converting equations to Cartesian coordinates.
This is a circle of radius \(\left| a \right|\) and center \(\left( {a,0} \right)\). Note that \(a\) might be negative (as it was in our example above) and so the absolute value bars are required on the radius. They should not be used however on the center.
- \(r = 2b\sin \theta \).
This is similar to the previous one. It is a circle of radius \(\left| b \right|\) and center \(\left( {0,b} \right)\).
- \(r = 2a\cos \theta + 2b\sin \theta \).
This is a combination of the previous two and by completing the square twice it can be shown that this is a circle of radius \(\sqrt {{a^2} + {b^2}} \) and center \(\left( {a,b} \right)\). In other words, this is the general equation of a circle that isn’t centered at the origin.
The first one is a circle of radius 7 centered at the origin. The second is a circle of radius 2 centered at \(\left( {2,0} \right)\). The third is a circle of radius \(\frac{7}{2}\) centered at \(\left( {0, - \frac{7}{2}} \right)\). Here is the graph of the three equations.

Note that it takes a range of \(0 \le \theta \le 2\pi \) for a complete graph of \(r = a\) and it only takes a range of \(0 \le \theta \le \pi \) to graph the other circles given here. You can verify this with a quick table of values if you’d like to.
Cardioids and Limacons
These can be broken up into the following three cases.
- Cardioids : \(r = a \pm a\cos \theta \) and \(r = a \pm a\sin \theta \).
These have a graph that is vaguely heart shaped and always contain the origin.
- Limacons with an inner loop : \(r = a \pm b\cos \theta \) and \(r = a \pm b\sin \theta \) with \(a < b\).
These will have an inner loop and will always contain the origin.
- Limacons without an inner loop : \(r = a \pm b\cos \theta \) and \(r = a \pm b\sin \theta \) with \(a > b\).
These do not have an inner loop and do not contain the origin.
These will all graph out once in the range \(0 \le \theta \le 2\pi \). Here is a table of values for each followed by graphs of each.
| \(\theta \) | \(r = 5 - 5\sin \theta \) | \(r = 7 - 6\cos \theta \) | \(r = 2 + 4\cos \theta \) |
|---|---|---|---|
| 0 | 5 | 1 | 6 |
| \(\displaystyle \frac{\pi }{2}\) | 0 | 7 | 2 |
| \(\pi \) | 5 | 13 | -2 |
| \(\displaystyle \frac{{3\pi }}{2}\) | 10 | 7 | 2 |
| \(2\pi \) | 5 | 1 | 6 |



There is one final thing that we need to do in this section. In the third graph in the previous example we had an inner loop. We will, on occasion, need to know the value of \(\theta \) for which the graph will pass through the origin. To find these all we need to do is set the equation equal to zero and solve as follows,
\[0 = 2 + 4\cos \theta \hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\,\,\,\,\,\cos \theta = - \frac{1}{2}\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}\theta = \frac{{2\pi }}{3},\frac{{4\pi }}{3}\]