Many of our applications in this chapter will revolve around minimum and maximum values of a function.  While we can all visualize the minimum and maximum values of a function we want to be a little more specific in our work here.  In particular we want to differentiate between two types of minimum or maximum values.  The following definition gives the types of minimums and/or maximums values that we’ll be looking at.

Definition

Note that when we say an “open interval around  ” we mean that we can find some interval , not including the endpoints, such that .  Or, in other words, c will be contained somewhere inside the interval and will not be either of the endpoints.

Also, we will collectively call the minimum and maximum points of a function the extrema of the function.  So, relative extrema will refer to the relative minimums and maximums while absolute extrema refer to the absolute minimums and maximums.

Now, let’s talk a little bit about the subtle difference between the absolute and relative in the definition above. 

We will have an absolute maximum (or minimum) at  provided f(c) is the largest (or smallest) value that the function will ever take on the domain that we are working on.  Also, when we say the “domain we are working on” this simply means the range of x’s that we have chosen to work with for a given problem.  There may be other values of x that we can actually plug into the function but have excluded them for some reason.

A relative maximum or minimum is slightly different.  All that’s required for a point to be a relative maximum or minimum is for that point to be a maximum or minimum in some interval of x’s around .  There may be larger or smaller values of the function at some other place, but relative to , or local to ,  f(c) is larger or smaller than all the other function values that are near it.

Note as well that in order for a point to be a relative extrema we must be able to look at function values on both sides of  to see if it really is a maximum or minimum at that point.  This means that relative extrema do not occur at the end points of a domain.  They can only occur interior to the domain.

There is actually some debate on the preceding point.  Some folks do feel that relative extrema can occur on the end points of a domain.  However, in this class we will be using the definition that says that they can’t occur at the end points of a domain.

It’s usually easier to get a feel for the definitions by taking a quick look at a graph.

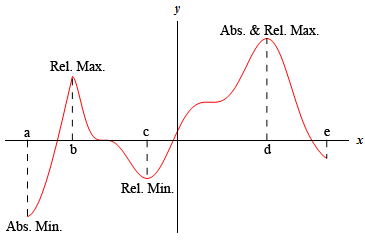
For the function shown in this graph we have relative maximums at  and .  Both of these point are relative maximums since they are interior to the domain shown and are the largest point on the graph in some interval around the point.  We also have a relative minimum at  since this point is interior to the domain and is the lowest point on the graph in an interval around it.  The far right end point, , will not be a relative minimum since it is an end point.

The function will have an absolute maximum at  and an absolute minimum at .  These two points are the largest and smallest that the function will ever be.  We can also notice that the absolute extrema for a function will occur at either the endpoints of the domain or at relative extrema.  We will use this idea in later sections so it’s more important than it might seem at the present time.

Let’s take a quick look at some examples to make sure that we have the definitions of absolute extrema and relative extrema straight.

As we saw in the previous example functions do not have to have relative extrema.  It is completely possible for a function to not have a relative maximum and/or a relative minimum.

As this example has shown there can only be a single absolute maximum or absolute minimum value, but they can occur at more than one place in the domain.

So, some graphs can have minimums but not maximums.  Likewise, a graph could have maximums but not minimums.

So, a function doesn’t have to have relative extrema as this example has shown.

As we’ve seen in the previous example functions don’t have to have any kind of extrema, relative or absolute.

As this example has shown a graph can in fact have extrema occurring at a large number (infinite in this case) of points.

We’ve now worked quite a few examples and we can use these examples to see a nice fact about absolute extrema.  First let’s notice that all the functions above were continuous functions.  Next notice that every time we restricted the domain to a closed interval (i.e. the interval contains its end points) we got absolute maximums and absolute minimums.  Finally, in only one of the three examples in which we did not restrict the domain did we get both an absolute maximum and an absolute minimum.

These observations lead us the following theorem.

Extreme Value Theorem

So, if we have a continuous function on an interval [a,b] then we are guaranteed to have both an absolute maximum and an absolute minimum for the function somewhere in the interval.  The theorem doesn’t tell us where they will occur or if they will occur more than once, but at least it tells us that they do exist somewhere.  Sometimes, all that we need to know is that they do exist.

This theorem doesn’t say anything about absolute extrema if we aren’t working on an interval.  We saw examples of functions above that had both absolute extrema, one absolute extrema, and no absolute extrema when we didn’t restrict ourselves down to an interval.

The requirement that a function be continuous is also required in order for us to use the theorem.  Consider the case of

Here’s the graph.

This function is not continuous at  as we move in towards zero the function is approaching infinity.  So, the function does not have an absolute maximum.  Note that it does have an absolute minimum however.  In fact the absolute minimum occurs twice at both  and .

If we changed the interval a little to say,

the function would now have both absolute extrema.  We may only run into problems if the interval contains the point of discontinuity.  If it doesn’t then the theorem will hold.

We should also point out that just because a function is not continuous at a point that doesn’t mean that it won’t have both absolute extrema in an interval that contains that point.  Below is the graph of a function that is not continuous at a point in the given interval and yet has both absolute extrema.

This graph is not continuous at , yet it does have both an absolute maximum (  ) and an absolute minimum (  ).  Also note that, in this case one of the absolute extrema occurred at the point of discontinuity, but it doesn’t need to.  The absolute minimum could just have easily been at the other end point or at some other point interior to the region.  The point here is that this graph is not continuous and yet does have both absolute extrema

The point of all this is that we need to be careful to only use the Extreme Value Theorem when the conditions of the theorem are met and not misinterpret the results if the conditions aren’t met. 

In order to use the Extreme Value Theorem we must have an interval and the function must be continuous on that interval.  If we don’t have an interval and/or the function isn’t continuous on the interval then the function may or may not have absolute extrema.

We need to discuss one final topic in this section before moving on to the first major application of the derivative that we’re going to be looking at in this chapter.

Fermat’s Theorem

Note that we can say that  because we are also assuming that  exists.

This theorem tells us that there is a nice relationship between relative extrema and critical points.  In fact it will allow us to get a list of all possible relative extrema.  Since a relative extrema must be a critical point the list of all critical points will give us a list of all possible relative extrema.

Consider the case of .  We saw that this function had a relative minimum at  in several earlier examples.  So according to Fermat’s theorem  should be a critical point.  The derivative of the function is,

Sure enough  is a critical point.

Be careful not to misuse this theorem.  It doesn’t say that a critical point will be a relative extrema.  To see this, consider the following case.

Clearly  is a critical point.  However we saw in an earlier example this function has no relative extrema of any kind.  So, critical points do not have to be relative extrema.

Also note that this theorem says nothing about absolute extrema.  An absolute extrema may or may not be a critical point.

To see the proof of this theorem see the Proofs From Derivative Applications section of the Extras chapter.