In this section we are going to take a quick look at
circles. However, before we do that we
need to give a quick formula that hopefully you’ll recall seeing at some point
in the past.
Given two points 
and the distance between them is given by,
So, why did we remind you of this formula? Well, let’s recall just what a circle
is. A circle is all the points that are
the same distance, r called the radius, from a point, - called the center. In other words, if is any point that is on the circle then it has
a distance of r from the center, .
If we use the distance formula on these two points we would
get,
Or, if we square both sides we get,
This is the standard
form of the equation of a circle with radius r and center .
Do not square out the two terms on the left. Leaving these terms as they are will allow us
to quickly identify the equation as that of a circle and to quickly identify
the radius and center of the circle.
Graphing circles is a fairly simple process once we know the
radius and center. In order to graph a
circle all we really need is the right most, left most, top most and bottom
most points on the circle. Once we know
these it’s easy to sketch in the circle.
Nicely enough for us these points are easy to find. Since these are points on the circle we know
that they must be a distance of r
from the center. Therefore the points
will have the following coordinates.
In other words all we need to do is add r on to the x coordinate
or y coordinate of the point to get
the right most or top most point respectively and subtract r from the x coordinate
or y coordinate to get the left most
or bottom most points.
Let’s graph some circles.
|
Example 2 Determine
the center and radius of each of the following circles and sketch the graph
of the circle.
(a) [Solution]
(b) [Solution]
(c) [Solution]
Solution
In all of these all that we really need to do is compare
the equation to the standard form and identify the radius and center. Once that is done find the four points
talked about above and sketch in the circle.
(a)
In this case it’s just x
and y squared by themselves. The only way that we could have this is to
have both h and k be zero. So, the center and radius is,
Don’t forget that the radius is the square root of the
number on the other side of the equal sign.
Here is a sketch of this circle.
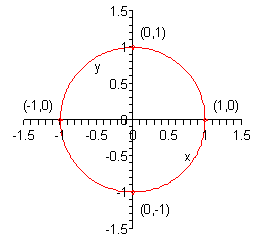
A circle centered at the origin with radius 1 (i.e. this circle) is called the unit circle. The unit circle is very useful in a
Trigonometry class.
[Return to Problems]
(b)
In this part, it looks like the x coordinate of the center is zero as with the previous
part. However, this time there is
something more with the y term and
so comparing this term to the standard form of the circle we can see that the
y coordinate of the center must be
3. The center and radius of this
circle is then,
Here is a sketch of the circle. The center is marked with a red cross in
this graph.
[Return to Problems]
(c)
For this part neither of the coordinates of the center are
zero. By comparing our equation with
the standard form it’s fairly easy to see (hopefully…) that the x coordinate of the center is 1. The y
coordinate isn’t too bad either, but we do need to be a little careful. In this case the term is and in the standard form the term is . Note that the signs are different. The only way that this can happen is if k is negative. So, the y
coordinate of the center must be -4.
The center and radius for this circle are,
Here is a sketch of this circle with the center marked
with a red cross.
[Return to Problems]
|
So, we’ve seen how to deal with circles that are already in
the standard form. However, not all
circles will start out in the standard form.
So, let’s take a look at how to put a circle in the standard form.
|
Example 3 Determine
the center and radius of each of the following.
(a) [Solution]
(b) [Solution]
Solution
Neither of these equations are in standard form and so to
determine the center and radius we’ll need to put it into standard form. We actually already know how to do
this. Back when we were solving
quadratic equations we saw a way to turn a quadratic polynomial into a
perfect square. The process was called
completing the square.
This is exactly what we want to do here, although in this
case we aren’t solving anything and we’re going to have to deal with the fact
that we’ve got both x and y in the equation. Let’s
step through the process with the first part.
(a)
We’ll go through the process in a step by step fashion
with this one.
Step 1 : First
get the constant on one side by itself and at the same time group the x terms together and the y terms together.
In this case there was only one term with a y in it and two with x’s in them.
Step 2 : For
each variable with two terms complete the square on those terms.
So, in this case that means that we only need to complete
the square on the x terms. Recall how this is done. We first take half the coefficient of the x and square it.
We then add this to both sides of the equation.
Now, the first three terms will factor as a perfect
square.
Step 3 : This is now the standard form of the
equation of a circle and so we can pick the center and radius right off
this. They are,
[Return to Problems]
(b)
In this part we’ll go through the process a little
quicker. First get terms properly
grouped and placed.
Now, as noted above we’ll need to complete the square
twice here, once for the x terms
and once for the y terms. Let’s first get the numbers that we’ll need
to add to both sides.
Now, add these to both sides of the equation.
When adding the numbers to both sides make sure and place
them properly. This means that we need
to put the number from the coefficient of the x with the x terms and
the number from the coefficient of the y
with the y terms. This placement is important since this will
be the only way that the quadratics will factor as we need them to factor.
Now, factor the quadratics as show above. This will give the standard form of the
equation of the circle.
This looks a little messier than the equations that we’ve
seen to this point. However, this is
something that will happen on occasion so don’t get excited about it. Here is the center and radius for this circle.
Do not get excited about the messy radius or fractions in
the center coordinates.
[Return to Problems]
|