In this section we’re going to take a look at Fourier cosine
series. We’ll start off much as we did
in the previous section where we looked at Fourier sine series. Let’s start by assuming that the function, 
,
we’ll be working with initially is an even function (i.e. ) and that we want to write a series
representation for this function on in terms of cosines (which are also
even). In other words we are going to
look for the following,
This series is called a Fourier
cosine series and note that in this case (unlike with Fourier sine series)
we’re able to start the series representation at since that term will not be zero as it was
with sines. Also, as with Fourier Sine
series, the argument of in the cosines is being used only because it
is the argument that we’ll be running into in the next chapter. The only real requirement here is that the
given set of functions we’re using be orthogonal on the interval we’re working
on.
Note as well that we’re assuming that the series will in
fact converge to on at this point.
In a later section we’ll be
looking into the convergence of this series in more detail.
So, to determine a formula for the coefficients, ,
we’ll use the fact that do form an orthogonal set on the interval as we showed in a previous
section. In that section we also derived
the following formula that we’ll need in a bit.
We’ll get a formula for the coefficients in almost exactly
the same fashion that we did in the previous section. We’ll start with the representation above and
multiply both sides by where m
is a fixed integer in the range . Doing this gives,
Next, we integrate both sides from to and as we were able to do with the Fourier
Sine series we can again interchange the integral and the series.
We now know that the all of the integrals on the right side
will be zero except when because the set of cosines form an orthogonal
set on the interval . However, we need to be careful about the
value of m (or n depending on the letter you want to use). So, after evaluating all of the integrals we
arrive at the following set of formulas for the coefficients.
:
:
Summarizing everything up then, the Fourier cosine series of
an even function, on is given by,
Finally, before we work an example, let’s notice that
because both and the cosines are even the integrand in both
of the integrals above is even and so we can write the formulas for the ’s as follows,
Now let’s take a look at an example.
|
Example 1 Find
the Fourier cosine series for on .
Solution
We clearly have an even function here and so all we really
need to do is compute the coefficients and they are liable to be a little
messy because we’ll need to do integration by parts twice. We’ll leave most of the actual integration
details to you to verify.
The
coefficients are then,
The Fourier
cosine series is then,
Note that we’ll
often strip out the from the series as we’ve done here because
it will almost always be different from the other coefficients and it allows
us to actually plug the coefficients into the series.
|
Now, just as we did in the previous section let’s ask what
we need to do in order to find the Fourier cosine series of a function that is
not even. As with Fourier sine series
when we make this change we’ll need to move onto the interval now instead of and again we’ll assume that the series will
converge to at this point and leave the discussion of the
convergence of this series to a later section.
We could go through the work to find the coefficients here
twice as we did with Fourier sine series, however there’s no real reason
to. So, while we could redo all the work
above to get formulas for the coefficients let’s instead go straight to the
second method of finding the coefficients.
In this case, before we actually proceed with this we’ll
need to define the even extension of a function, on . So, given a function we’ll define the even extension of the
function as,
Showing that this is an even function is simple enough.
and we can see that on and if is already an even function we get on .
Let’s take a look at some functions and sketch the even
extensions for the functions.
|
Example 2 Sketch
the even extension of each of the given functions.
(a) on [Solution]
(b) on [Solution]
(c) [Solution]
Solution
(a) on
Here is the even extension of this function.
Here is the graph of both the original function and its
even extension. Note that we’ve put
the “extension” in with a dashed line to make it clear the portion of the
function that is being added to allow us to get the even extension
[Return to Problems]
(b) on
The even extension of this function is,
The sketch of the function and the even extension is,
[Return to Problems]
(c)
Here is the even extension of this function,
The sketch of
the function and the even extension is,
[Return to Problems]
|
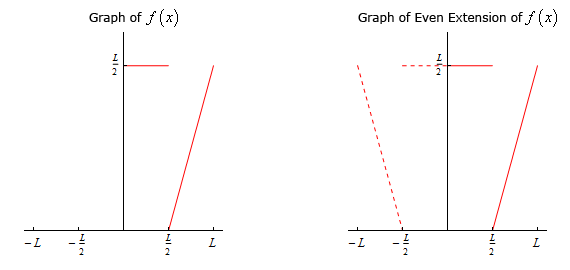
Okay, let’s now think about how we can use the even
extension of a function to find the Fourier cosine series of any function on .
So, given a function we’ll let be the even extension as defined above. Now, is an even function on and so we can write down its Fourier cosine
series. This is,
and note that we’ll use the second form of the integrals to
compute the constants.
Now, because we know that on we have and so the Fourier cosine series of on is also given by,
Let’s take a look at a couple of examples.
|
Example 3 Find
the Fourier cosine series for on .
Solution
All we need to do is compute the coefficients so here is
the work for that,
The Fourier
cosine series is then,
Note that as we
did with the first example in this section we stripped out the term before we plugged in the coefficients.
|
Next, let’s find the Fourier cosine series of an odd
function. Note that this is doable
because we are really finding the Fourier cosine series of the even extension
of the function.
|
Example 4 Find
the Fourier cosine series for on .
Solution
The integral for is simple enough but the integral for the
rest will be fairly messy as it will require three integration by parts. We’ll leave most of the details of the
actual integration to you to verify.
Here’s the work,
The Fourier
cosine series for this function is then,
|
Finally, let’s take a quick look at a piecewise function.
|
Example 5 Find
the Fourier cosine series for on .
Solution
We’ll need to split up the integrals for each of the
coefficients here. Here are the
coefficients.
For the rest of
the coefficients here is the integral we’ll need to do.
To make life a
little easier let’s do each of these separately.
Putting these
together gives,
So, after all
that work the Fourier cosine series is then,
|
Note that much as we saw with the Fourier sine series many
of the coefficients will quite messy to deal with.