There’s not much to do with this one.  Just divide both sides by 2 and then go to the unit circle.

So, we are looking for all the values of t for which cosine will have the value of .  So, let’s take a look at the following unit circle. 

From quick inspection we can see that  is a solution.  However, as I have shown on the unit circle there is another angle which will also be a solution.  We need to determine what this angle is.  When we look for these angles we typically want positive angles that lie between 0 and .  This angle will not be the only possibility of course, but by convention we typically look for angles that meet these conditions. 

To find this angle for this problem all we need to do is use a little geometry.  The angle in the first quadrant makes an angle of  with the positive x-axis, then so must the angle in the fourth quadrant.  So we could use , but again, it’s more common to use positive angles so, we’ll use .

We aren’t done with this problem.  As the discussion about finding the second angle has shown there are many ways to write any given angle on the unit circle.  Sometimes it will be  that we want for the solution and sometimes we will want both (or neither) of the listed angles.  Therefore, since there isn’t anything in this problem (contrast this with the next problem) to tell us which is the correct solution we will need to list ALL possible solutions. 

This is very easy to do.  Go back to my introduction in the Trig Function Evaluation section and you’ll see there that I used

to represent all the possible angles that can end at the same location on the unit circle, i.e. angles that end at .  Remember that all this says is that we start at  then rotate around in the counter-clockwise direction (n is positive) or clockwise direction (n is negative) for n complete rotations.  The same thing can be done for the second solution.

So, all together the complete solution to this problem is

As a final thought, notice that we can get  by using  in the second solution.

This problem is almost identical to the previous except now I want all the solutions that fall in the interval .  So we will start out with the list of all possible solutions from the previous problem.

Then start picking values of n until we get all possible solutions in the interval.

First notice that since both the angles are positive adding on any multiples of  (n positive) will get us bigger than  and hence out of the interval.  So, all positive values of n are immediately out.  Let’s take a look at the negatives values of n.

These are both greater than  and so are solutions, but if we subtract another  off (i.e use  ) we will once again be outside of the interval.

So, the solutions are : .

This one is very similar to Problem 1, although there is a very important difference.  We’ll start this problem in exactly the same way as we did in Problem 1.

So, we are looking for angles that will give  out of the sine function.  Let’s again go to our trusty unit circle.

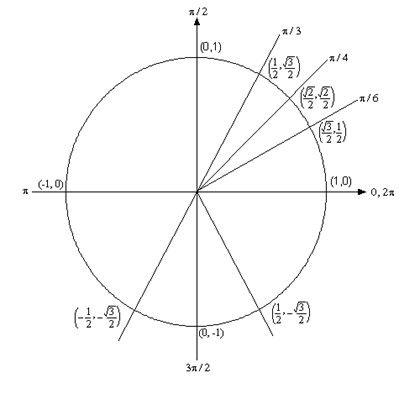
Now, there are no angles in the first quadrant for which sine has a value of .  However, there are two angles in the lower half of the unit circle for which sine will have a value of .  So, what are these angles?  A quick way of doing this is to, for a second, ignore the “-” in the problem and solve  in the first quadrant only.  Doing this give a solution of . Now, again using some geometry, this tells us that the angle in the third quadrant will be  below the negative x-axis or .  Likewise, the angle in the fourth quadrant will  below the positive x-axis or .  Remember that we’re looking for positive angles between 0 and .

Now we come to the very important difference between this problem and Problem 1.  The solution is NOT

This is not the set of solutions because we are NOT looking for values of x for which , but instead we are looking for values of x for which .  Note the difference in the arguments of the sine function!  One is x and the other is .  This makes all the difference in the world in finding the solution! Therefore, the set of solutions is

Well, actually, that’s not quite the solution.  We are looking for values of x so divide everything by 5 to get.

Notice that I also divided the  by 5 as well!  This is important!  If you don’t do that you WILL miss solutions.  For instance, take .

I’ll leave it to you to verify my work showing they are solutions.  However it makes the point.  If you didn’t divided the  by 5 you would have missed these solutions!

This problem is almost identical to the previous problem except this time we have an argument of  instead of .  However, most of the problem is identical.  In this case the solutions we get will be

Notice the difference in the left hand sides between this solution and the corresponding solution in the previous problem.

Now we need to solve for x.  We’ll first subtract 4 from both sides then divide by 5 to get the following solution.

It’s somewhat messy, but it is the solution.  Don’t get excited when solutions get messy.  They will on occasion and you need to get used to seeing them.

I’m going to leave most of the explanation that was in the previous three out of this one to see if you have caught on how to do these.

By examining a unit circle we see that

Or, upon dividing by 3,

Now, we are looking for solutions in the range .  So, let’s start trying some values of n.

 :                                                                                              

 :

 :

Once, we’ve hit the limit in one direction there’s no reason to continue on.  In, other words if using  gets values larger than  then so will all values of n larger than 2.  Note as well that it is possible to have one of these be a solution and the other to not be a solution.  It all depends on the interval being used.

Let’s not forget the negative values of n.

 :

 :

Again, now that we’ve started getting less than  all other values of  will also give values that are less than .

So putting all this together gives the following six solutions.

Finally, note again that if we hadn’t divided the  by 3 the only solutions we would have gotten would be  and .  We would have completely missed four of the solutions!

This one doesn’t actually have a lot of work involved.  We’re looking for values of t for which .  This is one of the few trig equations for which there is only a single angle in all of  which will work.  So our solutions are

Or, by dividing by 4,

Since we want the solutions on  negative values of n aren’t needed for this problem.  So, plugging in values of n will give the following four solutions

This is a trick question that is designed to remind you of certain properties about sine and cosine.  Recall that  and .  Therefore, since cosine will never be greater that 1 it definitely can’t be 2.  So THERE ARE NO SOLUTIONS to this equation!

This problem is a little different from the previous ones.  First, we need to do some rearranging and simplification.

So, solving  is the same as solving .   At some level we didn’t need to do this for this problem as all we’re looking for is angles in which sine and cosine have the same value, but opposite signs.  However, for other problems this won’t be the case and we’ll want to convert to tangent.

Looking at our trusty unit circle it appears that the solutions will be,

Or, upon dividing by the 2 we get the solutions

No interval was given so we’ll stop here.

Again, we need to do a little work to get this equation into a form we can handle.  The easiest way to do this one is to recall one of the trig formulas from the Trig Formulas section (in particular Problem 3).

At this point, proceed as we did in the previous problems..

Or, by dividing by 2,

Again, there is no interval so we stop here.

This problem is very different from the previous problems. 

DO NOT DIVIDE BOTH SIDES BY A COSINE!!!!!! 

If you divide both sides by a cosine you WILL lose solutions!  The best way to deal with this one is to “factor” the equations as follows.

So, solutions will be values of w for which

or,

In the first case we will have  at the following values.

In the second case we will have  at the following values.

Note that in this case we got a repeat answer.  Sometimes this will happen and sometimes it won’t so don’t expect this to always happen.  So, all together we get the following solutions,

As with the previous couple of problems this has no interval so we’ll stop here.  Notice as well that if we’d divided out a cosine we would have lost half the solutions.

This problem appears very difficult at first glance, but only the first step is different for the previous problems.  First notice that

The solutions to this are  and .  So, why cover this?  Well, if you think about it there is very little difference between this and the problem you are asked to do.  First, we factor the equation

The solutions to this are

The solutions to the first are

Or, upon dividing by 3,

The second has no solutions because cosine can’t be less that -1.  Don’t get used to this.  Often both will yield solutions!

Therefore, the solutions to this are (again no interval so we’re done at this point).

This problem, in some ways, is VERY different from the previous problems and yet will work in essentially the same manner.  To this point all the problems came down to a few “basic” angles that most people know and/or have used on a regular basis.  This problem won’t, but the solution process is pretty much the same.  First, get the sine on one side by itself.

Now, at this point we know that we don’t have one of the “basic” angles since those all pretty much come down to having 0, 1, ,  or  on the right side of the equal sign.  So, in order to solve this we’ll need to use our calculator.  Every calculator is different, but most will have an inverse sine (  ), inverse cosine (  ) and inverse tangent (  ) button on them these days.  If you aren’t familiar with inverse trig functions see the next section in this review.  Also, make sure that your calculator is set to do radians and not degrees for this problem.

It is also very important to understand the answer that your calculator will give.  First, note that I said answer (i.e. a single answer) because that is all your calculator will ever give and we know from our work above that there are infinitely many answers.  Next, when using your calculator to solve , i.e. using , we will get the following ranges for x.

So, when using the inverse sine button on your calculator it will ONLY return answers in the first or fourth quadrant depending upon the sign of a.

Using our calculator in this problem yields,

Don’t forget the 2 that is in the argument!  We’ll take care of that in a bit.

Now, we know from our work above that if there is a solution in the first quadrant to this equation then there will also be a solution in the second quadrant and that it will be at an angle of 0.2013579 above the x-axis as shown below.

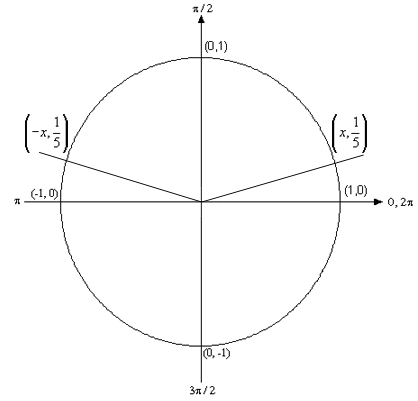
I didn’t put in the x, or cosine value, in the unit circle since it’s not needed for the problem.  I did however not that they will be the same value, except for the negative sign.  The angle in the second quadrant will then be,

So, let’s put all this together.

Note that I added the  onto our angles as well since we know that will be needed in order to get all the solutions.  The final step is to then divide both sides by the 2 in order to get all possible solutions.  Doing this gives,

The answers won’t be as “nice” as the answers in the previous problems but there they are.  Note as well that if we’d been given an interval we could plug in values of n to determine the solutions that actually fall in the interval that we’re interested in.

This problem is again very similar to previous problems and yet has some differences.  First get the cosine on one side by itself.

Now, let’s take a quick look at a unit circle so we can see what angles we’re after.

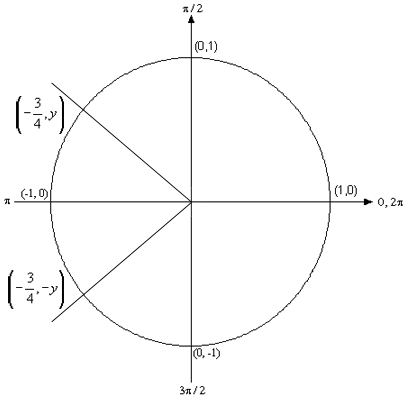
I didn’t put the y values in since they aren’t needed for this problem.  Note however, that they will be the same except have opposite signs.  Now, if this were a problem involving a “basic” angle we’d drop the “-” to determine the angle each of the lines above makes with the x-axis and then use that to find the actual angles.  However, in this case since we’re using a calculator we’ll get the angle in the second quadrant for free so we may as well jump straight to that one. 

However, prior to doing that let’s acknowledge how the calculator will work when working with inverse cosines.  If we’re going to solve , using , then our calculator will give one answer in one of the following ranges, depending upon the sign of a.

So, using our calculator we get the following angle in the second quadrant.

Now, we need to get the second angle that lies in the third quadrant.  To find this angle note that the line in the second quadrant and the line in the third quadrant both make the same angle with the negative x-axis.  Since we know what the angle in the second quadrant is we can find the angle that this line makes with the negative x-axis as follows,

This means that the angle in the third quadrant is,

Putting all this together gives,

Finally, we just need to multiply both sides by 5 to determine all possible solutions.

We’ll do this one much quicker than the previous two.  First get the sine on one side by itself.

From a unit circle we can see that the two angles we’ll be looking for are in the third and fourth quadrants.  Our calculator will give us the angle that is in the fourth quadrant and this angle is,

Note that in all the previous examples we generally wouldn’t have used this answer because it is negative.  There is nothing wrong with the answer, but as I mentioned several times in earlier problems we generally try to use positive angles between 0 and .  However, in this case since we are doing calculator work we won’t worry about that fact that it’s negative.  If we wanted the positive angle we could always get it as,

Now, the line corresponding to this solution makes an angle with the positive x-axis of 0.775395.  The angle in the third quadrant will be 0.775395 radians below the negative x-axis and so is,

Putting all this together gives,

To get the final solution all we need to do is add 2 to both sides.  All possible solutions are then,