You can navigate through this E-Book using the menu to the left. For E-Books that have a Chapter/Section organization each option in the menu to the left indicates a chapter and will open a menu showing the sections in that chapter. Alternatively, you can navigate to the next/previous section or chapter by clicking the links in the boxes at the very top and bottom of the material.
Also, depending upon the E-Book, it will be possible to download the complete E-Book, the chapter containing the current section and/or the current section. You can do this be clicking on the E-Book, Chapter, and/or the Section link provided below.
For those pages with mathematics on them you can, in most cases, enlarge the mathematics portion by clicking on the equation. Click the enlarged version to hide it.
In this section we’re going to take a look at some more
volume problems. However, the problems
we’ll be looking at here will not be solids of revolution as we looked at in
the previous two sections. There are
many solids out there that cannot be generated as solids of revolution, or at
least not easily and so we need to take a look at how to do some of these
problems.
Now, having said that these will not be solids of
revolutions they will still be worked in pretty much the same manner. For each solid we’ll need to determine the
cross-sectional area, either 
or ,
and they use the formulas we used in the previous two sections,
The “hard” part of these problems will be determining what
the cross-sectional area for each solid.
Each problem will be different and so each cross-sectional area will be
determined by different means.
Also, before we proceed with any examples we need to
acknowledge that the integrals in this section might look a little tricky at
first. There are going to be very few
numbers in these problems. All of the
examples in this section are going to be more general derivation of volume
formulas for certain solids. As such
we’ll be working with things like circles of radius r and we’ll not be giving a specific value of r and we’ll have heights of h
instead of specific heights, etc.
All the letters in the integrals are going to make the
integrals look a little tricky, but all you have to remember is that the r’s and the h’s are just letters being used to represent a fixed quantity for
the problem, i.e. it is a
constant. So when we integrate we only
need to worry about the letter in the differential as that is the variable
we’re actually integrating with respect to.
All other letters in the integral should be thought of as
constants. If you have trouble doing
that, just think about what you’d do if the r
was a 2 or the h was a 3 for example.
Let’s start with a simple example that we don’t actually
need to do an integral that will illustrate how these problems work in general
and will get us used to seeing multiple letters in integrals.
|
Example 1 Find
the volume of a cylinder of radius r
and height h.
Solution
Now, as we mentioned before starting this example we
really don’t need to use an integral to find this volume, but it is a good
example to illustrate the method we’ll need to use for these types of
problems.
We’ll start off with the sketch of the cylinder below.
We’ll center the cylinder on the x-axis and the cylinder will start at and end at as shown.
Note that we’re only choosing this particular set up to get an
integral in terms of x and to make
the limits nice to deal with. There
are many other orientations that we could use.
What we need here is to get a formula for the
cross-sectional area at any x. In this case the cross-sectional area is
constant and will be a disk of radius r. Therefore, for any x we’ll have the following cross-sectional area,
Next the limits for the integral will be since that is the range of x in which the cylinder lives. Here is the integral for the volume,
So, we get the
expected formula.
Also, recall we
are using r to represent the radius
of the cylinder. While r can clearly take different values it
will never change once we start the problem.
Cylinders do not change their radius in the middle of a problem and so
as we move along the center of the cylinder (i.e. the x-axis) r is a fixed number and won’t
change. In other words it is a
constant that will not change as we change the x. Therefore, because we
integrated with respect to x the r will be a constant as far as the
integral is concerned. The r can then be pulled out of the
integral as shown (although that’s not required, we just did it to make the
point). At this point we’re just
integrating dx and we know how to
do that.
When we
evaluate the integral remember that the limits are x values and so we plug into the x and NOT the r. Again, remember that r is just a letter that is being used
represent the radius of the cylinder and, once we start the integration, is
assumed to be a fixed constant.
As noted before
we started this example if you’re having trouble with the r just think of what you’d do if there
was a 2 there instead of an r. In this problem, because we’re integrating
with respect to x, both the 2 and
the r will behave in the same
manner. Note however that you should
NEVER actually replace the r with a
2 as that WILL lead to a wrong answer.
You should just think of what you would do IF the r was a 2.
|
So, to work these problems we’ll first need to get a sketch
of the solid with a set of x and y axes to help us see what’s going on. At the very least we’ll need the sketch to
get the limits of the integral, but we will often need it to see just what the
cross-sectional area is. Once we have
the sketch we’ll need to determine a formula for the cross-sectional area and
then do the integral.
Let’s work a couple of more complicated examples. In these examples the main issue is going to
be determining what the cross-sectional areas are.
|
Example 2 Find
the volume of a pyramid whose base is a square with sides of length L and whose height is h.
Solution
Let’s start off with a sketch of the pyramid. In this case we’ll center the pyramid on
the y-axis and to make the
equations easier we are going to position the point of the pyramid at the
origin.
Now, as shown here the cross-sectional area will be a
function of y and it will also be a
square with sides of length s. The area of the square is easy, but we’ll
need to get the length of the side in terms of y. To determine this
consider the figure on the right above.
If we look at the pyramid directly from the front we’ll see that we
have two similar triangles and we know that the ratio of any two sides of
similar triangles must be equal. In
other words, we know that,
So, the
cross-sectional area is then,
The limit for
the integral will be and the volume will be,
Again, do not get excited about the L and the h in the
integral. Once we start the problem if
we change y they will not change
and so they are constants as far as the integral is concerned and can get
pulled out of the integral. Also,
remember that when we evaluate will only plug the limits into the variable we
integrated with respect to, y in
this case.
|
Before we proceed with some more complicated examples we
should once again remind you to not get excited about the other letters in the
integrals. If we’re integrating with
respect to x or y then all other letters in the formula that represent fixed quantities
(i.e. radius, height, length of a
side, etc.) are just constants and
can be treated as such when doing the integral.
Now let’s do some more examples.
|
Example 3 For
a sphere of radius r find the
volume of the cap of height h.
Solution
A sketch is probably best to illustrate what we’re after
here.
We are after the top portion of the sphere and the height
of this is portion is h. In this case we’ll use a cross-sectional
area that starts at the bottom of the cap, which is at ,
and moves up towards the top, which is at . So, each cross-section will be a disk of
radius x. It is a little easier to see that the
radius will be x if we look at it
from the top as shown in the sketch to the right above. The area of this disk is then,
This is a problem however as we need the cross-sectional
area in terms of y. So, what we really need to determine what will be for any given y at the cross-section. To
get this let’s look at the sphere from the front.
In particular look at the triangle POR. Because the point R lies on the sphere itself we can see
that the length of the hypotenuse of this triangle (the line OR) is r, the radius of the sphere.
The line PR has a length of x and the line OP has length y so by
the Pythagorean Theorem we know,
So, we now know
what will be for any given y and so the cross-sectional area is,
As we noted
earlier the limits on y will be and so the volume is,
|
In the previous example we again saw an r in the integral. However,
unlike the previous two examples it was not multiplied times the x or the y and so could not be pulled out of the integral. In this case it was like we were integrating and we know how integrate that. So, in this case we need to treat the like the 4 and so when we integrate that we’ll
pick up a y.
|
Example 4 Find
the volume of a wedge cut out of a cylinder of radius r if the angle between the top and bottom of the wedge is .
Solution
We should really start off with a sketch of just what
we’re looking for here.
On the left we see how the wedge is being cut out of the
cylinder. The base of the cylinder is
the circle give by and the angle between this circle and the
top of the wedge is . The sketch in the upper right position is
the actual wedge itself. Given the
orientation of the axes here we get the portion of the circle with positive y and so we can write the equation of
the circle as since we only need the positive y values. Note as well that this is the reason for
the way we oriented the axes here. We
get positive y’s and we can write
the equation of the circle as a function only of x’s.
Now, as we can see in the two sketches of the wedge the
cross-sectional area will be a right triangle and the area will be a function
of x as we move from the back of
the cylinder, at ,
to the front of the cylinder, at .
The right angle of the triangle will be on the circle
itself while the point on the x-axis
will have an interior angle of . The base of the triangle will have a length
of y and using a little right
triangle trig we see that the height of the rectangle is,
So, we now know
the base and height of our triangle, in terms of y, and we have an equation for y in terms of x and so
we can see that the area of the triangle, i.e.
the cross-sectional area is,
The limits on x are and so the volume is then,
|
The next example is very similar to the previous one except
it can be a little difficult to visualize the solid itself.
|
Example 5 Find
the volume of the solid whose base is a disk of radius r and whose cross-sections are equilateral triangles.
Solution
Let’s start off with a couple of sketches of this
solid. The sketch on the left is from
the “front” of the solid and the sketch on the right is more from the top of
the solid.
The base of this solid is the disk of radius r and we move from the back of the
disk at to the front of the disk at we form equilateral triangles to form the
solid. A sample equilateral triangle,
which is also the cross-sectional area, is shown above to hopefully make it a
little clearer how the solid is formed.
Now, let’s get a formula for the cross-sectional
area. Let’s start with the two
sketches below.
In the left hand sketch we are looking at the solid from
directly above and notice that we “reoriented” the sketch a little to put the
x and y-axis in the “normal” orientation. The solid vertical line in this sketch is
the cross-sectional area. From this we
can see that the cross-section occurs at a given x and the top half will have a length of y where the value of y
will be the y-coordinate of the
point on the circle and so is,
Also, because the cross-section is an equilateral triangle
that is centered on the x-axis the
bottom half will also have a length of y. Thus the base of the cross-section must
have a length of 2y.
The sketch to the right is of one of the
cross-sections. As noted above the
base of the triangle has a length of 2y. Also note that because it is an equilateral
triangle the angles are all . If we divide the cross-section in two (as
shown with the dashed line) we now have two right triangles and using right
triangle trig we can see that the length of the dashed line is,
Therefore the
height of the cross-section is . Because the cross-section is a triangle we
know that that it’s area must then be,
Note that we used the cross-sectional area in terms of x because each of the cross-sections
is perpendicular to the x-axis and
this pretty much forces us to integrate with respect to x.
The volume of the solid is then,
|
The final example we’re going to work here is a little
tricky both in seeing how to set it up and in doing the integral.
|
Example 6 Find
the volume of a torus with radii r
and R.
Solution
First, just what is a torus? A torus is a donut shaped solid that is
generated by rotating the circle of radius r and centered at (R,
0) about the y-axis. This is shown in the sketch to the left
below.
One of the trickiest parts of this problem is seeing what
the cross-sectional area needs to be.
There is an obvious one. Most
people would probably think of using the circle of radius r that we’re rotating about the y-axis as the cross-section. It is definitely one of the more obvious
choices, however setting up an integral using this is not so easy.
So, what we’ll do is use a cross-section as shown in the
sketch to the right above. If we cut
the torus perpendicular to the y-axis
we’ll get a cross-section of a ring and finding the area of that shouldn’t be
too bad. To do that let’s take a look
at the two sketches below.
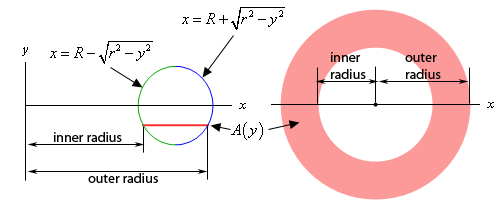
The sketch to the left is a sketch of the full
cross-section. The sketch to the left
is more important however. This is a
sketch of the circle that we are rotating about the y-axis. Included is a line
representing where the cross-sectional area would be in the torus.
Notice that the inner radius will always be the left
portion of the circle and the outer radius will always be the right portion
of the circle. Now, we know that the
equation of this is,
and so if we
solve for x we can get the
equations for the left and right sides as shown above in the sketch. This however means that we also now have
equations for the inner and outer radii.
The
cross-sectional area is then,
Next, the
lowest cross-section will occur at |