Paul's Online Math Notes
     
 
Online Notes / Differential Equations / Systems of DE`s / Modeling
Differential Equations

You can navigate through this E-Book using the menu to the left. For E-Books that have a Chapter/Section organization each option in the menu to the left indicates a chapter and will open a menu showing the sections in that chapter. Alternatively, you can navigate to the next/previous section or chapter by clicking the links in the boxes at the very top and bottom of the material.

Also, depending upon the E-Book, it will be possible to download the complete E-Book, the chapter containing the current section and/or the current section. You can do this be clicking on the E-Book, Chapter, and/or the Section link provided below.

For those pages with mathematics on them you can, in most cases, enlarge the mathematics portion by clicking on the equation. Click the enlarged version to hide it.
   
Laplace Transforms E-Book   Chapter   Section Series Solutions to DE's

In this section we’re going to go back and revisit the idea of modeling only this time we’re going to look at it in light of the fact that we now know how to solve systems of differential equations. 

 

We’re not actually going to be solving any differential equations in this section.  Instead we’ll just be setting up a couple of problems that are extensions of some of the work that we’ve done in earlier modeling sections whether it is the first order modeling or the vibrations work we did in the second order chapter.  Almost all of the systems that we’ll be setting up here will be nonhomogeneous systems (which we only briefly looked at), will be nonlinear (which we didn’t look at) and/or will involve systems with more than two differential equations (which we didn’t look at, although most of what we do know will still be true).

 

Mixing Problems

Let’s start things by looking at a mixing problem.  The last time we saw these was back in the first order chapter.  In those problems we had a tank of liquid with some type of contaminate dissolved in it.   Liquid, possibly with more contaminate dissolved in it, entered the tank and liquid left the tank.  In this situation we want to extend things out to the following situation.

Modeling_Mix_G1

We’ll now have two tanks that are interconnected with liquid potentially entering both and with an exit for some of the liquid if we need it (as illustrated by the lower connection).  For this situation we’re going to make the following assumptions.

 

  1. The inflow and outflow from each tank are equal, or in other words the volume in each tank is constant.  When we worked with a single tank we didn’t need to worry about this, but here if we don’t well end up with a system with nonconstant coefficients and those can be quite difficult to solve.

  2. The concentration of the contaminate in each tank is the same at each point in the tank.  In reality we know that this won’t be true but without this assumption we’d need to deal with partial differential equations.

  3. The concentration of contaminate in the outflow from tank 1 (the lower connection in the figure above) is the same as the concentration in tank 1.  Likewise, the concentration of contaminate in the outflow from tank 2 (the upper connection) is the same as the concentration in tank 2.

  4. The outflow from tank 1 is split and only some of the liquid exiting tank 1 actually reaches tank 2.  The remainder exits the system completely.  Note that if we don’t want any liquid to completely exit the system we can think of the exit as having a value that is turned off.  Also note that we could just as easily done the same thing for the outflow from tank 2 if we’d wanted to.

 

Let’s take a look at a quick example.

 

Example 1  Two 1000 liter tanks are with salt water.  Tank 1 contains 800 liters of water initially containing 20 grams of salt dissolved in it and tank 2 contains 1000 liters of water and initially has 80 grams of salt dissolved in it.  Salt water with a concentration of  gram/liter of salt enters tank 1 at a rate of 4 liters/hour.  Fresh water enters tank 2 at a rate of 7 liters/hour.  Through a connecting pipe water flows from tank 2 into tank 1 at a rate of 10 liters/hour.  Through a different connecting pipe 14 liters/hour flows out of tank 1 and 11 liters/hour are drained out of the pipe (and hence out of the system completely) and only 3 liters/hour flows back into tank 2.  Set up the system that will give the amount of salt in each tank at any given time. 

 

Solution

Okay, let  and  be the amount of salt in tank 1 and tank 2 at any time t respectively.  Now all we need to do is set up a differential equation for each tank just as we did back when we had a single tank.  The only difference is that we now need to deal with the fact that we’ve got a second inflow to each tank and the concentration of the second inflow will be the concentration of the other tank.

 

Recall that the basic differential equation is the rate of change of salt ( ) equals the rate at which salt enters minus the rate at salt leaves.  Each entering/leaving rate is found by multiplying the flow rate times the concentration.

 

Here is the differential equation for tank 1.

                      

 

In this differential equation the first pair of numbers is the salt entering from the external inflow.  The second set of numbers is the salt that entering into the tank from the water flowing in from tank 2.  The third set is the salt leaving tank as water flows out.

 

Here’s the second differential equation.

                      

 

Note that because the external inflow into tank 2 is fresh water the concentration of salt in this is zero.

 

In summary here is the system we’d need to solve,

                                        

 

This is a nonhomogeneous system because of the first term in the first differential equation.  If we had fresh water flowing into both of these we would in fact have a homogeneous system.

 

Population

The next type of problem to look at is the population problem.  Back in the first order modeling section we looked at some population problems.  In those problems we looked at a single population and often included some form of predation.  The problem in that section was we assumed that the amount of predation would be constant.  This however clearly won’t be the case in most situations.  The amount of predation will depend upon the population of the predators and the population of the predators will depend, as least partially, upon the population of the prey.

 

So, in order to more accurately (well at least more accurate than what we originally did) we really need to set up a model that will cover both populations, both the predator and the prey.  These types of problems are usually called predator-prey problems.  Here are the assumptions that we’ll make when we build up this model.

 

  1. The prey will grow at a rate that is proportional to its current population if there are no predators.

  2. The population of predators will decrease at a rate proportional to its current population if there is no prey.

  3. The number of encounters between predator and prey will be proportional to the product of the populations. 

  4. Each encounter between the predator and prey will increase the population of the predator and decrease the population of the prey.

 

So, given these assumptions let’s write down the system for this case.

 

Example 2  Write down the system of differential equations for the population of predators and prey using the assumptions above.    

 

Solution

We’ll start off by letting x represent the population of the predators and y represent the population of the prey.

 

Now, the first assumption tells us that, in the absence of predators, the prey will grow at a rate of  where .  Likewise the second assumption tells us that, in the absence of prey, the predators will decrease at a rate of  where .

 

Next, the third and fourth assumptions tell us how the population is affected by encounters between predators and prey.  So, with each encounter the population of the predators will increase at a rate of  and the population of the prey will decrease at a rate of  where  and .

 

Putting all of this together we arrive at the following system.

 

                                                    

 

Note that this is a nonlinear system and we’ve not (nor will we here) discuss how to solve this kind of system.  We simply wanted to give a “better” model for some population problems and to point out that not all systems will be nice and simple linear systems.

 

Mechanical Vibrations

When we first looked at mechanical vibrations we looked at a single mass hanging on a spring with the possibility of both a damper and/or an external force acting on the mass.  Here we want to look at the following situation.

Modeling_Vibration_G1

 

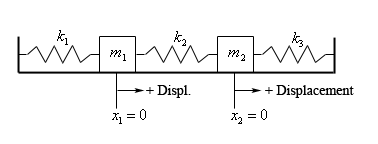
In the figure above we are assuming that the system is at rest.  In other words all three springs are currently at their natural lengths and are not exerting any forces on either of the two masses and that there are no currently any external forces acting on either mass.

 

We will use the following assumptions about this situation once we start the system in motion.

 

  1.  will measure the displacement of mass
     from its equilibrium (i.e. resting) position and
     will measure the displacement of mass
     from its equilibrium position.

  2. As noted in the figure above all displacement will be assumed to be positive if it is to the right of equilibrium position and negative if to the left of the equilibrium position.

  3. All forces acting to the right are positive forces and all forces acting to the left are negative forces.

  4. The spring constants,
    ,
    , and
    , are all positive and may or may not be the same value.

  5. The surface that the system is sitting on is frictionless and so the mass of each of the objects will not affect the system in any way.

 

Before writing down the system for this case recall that the force exerted by the spring on the each mass is the spring constant times the amount that the spring has been compressed or stretched and we’ll need to be careful with signs to make sure that the force is acting in the correct direction.

 

Example 3  Write down the system of differential equations for the spring and mass system above.         

 

Solution

To help us out let’s first take a quick look at a situation in which both of the masses have been moved.  This is shown below.

 

Modeling_Vibration_G2

Before proceeding let’s note that this is only a representation of a typical case, but most definitely not all possible cases. 

 

In this case we’re assuming that both  and  are positive and that , or in other words, both masses have been moved to the right of their respective equilibrium points and that  has been moved farther than .  So, under these assumption on   and  we know that the spring on the left (with spring constant  ) has been stretched past it’s natural length while the middle spring (spring constant  ) and the right spring (spring constant  ) are both under compression.

 

Also, we’ve shown the external forces,  and , as present and acting in the positive direction.  They do not, in practice, need to be present in every situation in which case we will assume that  and/or .  Likewise, if the forces are in fact acting in the negative direction we will then assume that  and/or .

 

Before proceeding we need to talk a little bit about how the middle spring will behave as the masses move.  Here are all the possibilities that we can have and the affect each will have on .  Note that in each case the amount of compression/stretch in the spring is given by  although we won’t be using the absolute value bars when we set up the differential equations.

 

1. If both mass move the same amount in the same direction then the middle spring will not have changed length and we’ll have . 

2. If both masses move in the positive direction then the sign of  will tell us which has moved more. If  moves more than  then the spring will be in compression and .  Likewise, if  moves more than  then the spring will have been stretched and .

3. If both masses move in the negative direction we’ll have pretty much the opposite behavior as #2.  If  moves more than  then the spring will have been stretched and .  Likewise, if  moves more than  then the spring will be in compression and .

4. If  moves in the positive direction and  moves in the negative direction then the spring will be in compression and .

5. Finally, if   moves in the negative direction and  moves in the positive direction then the spring will have been stretched and .

 

Now, we’ll use the figure above to help us develop the differential equations (the figure corresponds to case 2 above…) and then make sure that they will also hold for the other cases as well.

 

Let’s start off by getting the differential equation for the forces acting on .  Here is a quick sketch of the forces acting on  for the figure above.

Modeling_Vibration_G3

In this case  and so the first spring has been stretched and so will exert a negative (i.e. to the left) force on the mass.  The force from the first spring is then  and the “-” is needed because the force is negative but both  and  are positive.

 

Next, because we’re assuming that  has moved more than  and both have moved in the positive direction we also know that .  Because  has moved more than  we know that the second spring will be under compression and so the force should be acting in the negative direction on  and so the force will be .  Note that because  is positive and  is negative this force will have the correct sign (i.e. negative).

 

The differential equation for  is then,

                                               

 

Note that this will also hold for all the other cases.  If  has been moved in the negative direction the force form the spring on the right that acts on the mass will be positive and  will be a positive quantity in this case.  Next, if the middle is has been stretched (i.e.  ) then the force from this spring on  will be in the positive direction and  will be a positive quantity in this case.  Therefore, this differential equation holds for all cases not just the one we illustrated at the start of this problem.

 

Let’s now write down the differential equation for all the forces that are acting on .  Here is a sketch of the forces acting on this mass for the situation sketched out in the figure above.

Modeling_Vibration_G4

In this case  is positive and so the spring on the right is under compression and will exert a negative force on  and so this force should be , where the “-” is required because both  and  are positive.  Also, the middle spring is still under compression but the force that it exerts on this mass is now a positive force, unlike in the case of , and so is given by .  The “-” on this force is required because  is negative and the force must be positive.

 

The differential equation for  is then,

                                              

 

We’ll leave it to you to verify that this differential equation does in fact hold for all the other cases.

 

Putting all of this together and doing a little rewriting will then give the following system of differential equations for this situation.

 

                                               

 

This is a system to two linear second order differential equations that may or may not be nonhomogeneous depending whether there are any external forces,  and , acting on the masses.