Section 12.13 : Spherical Coordinates
In this section we will introduce spherical coordinates. Spherical coordinates can take a little getting used to. It’s probably easiest to start things off with a sketch.

Spherical coordinates consist of the following three quantities.
First there is \(\rho \). This is the distance from the origin to the point and we will require \(\rho \ge 0\).
Next there is \(\theta \). This is the same angle that we saw in polar/cylindrical coordinates. It is the angle between the positive \(x\)-axis and the line above denoted by \(r\) (which is also the same \(r\) as in polar/cylindrical coordinates). There are no restrictions on \(\theta \).
Finally, there is \(\varphi \). This is the angle between the positive \(z\)-axis and the line from the origin to the point. We will require \(0 \le \varphi \le \pi \).
In summary, \(\rho \) is the distance from the origin to the point, \(\varphi \) is the angle that we need to rotate down from the positive z-axis to get to the point and \(\theta \) is how much we need to rotate around the \(z\)-axis to get to the point.
We should first derive some conversion formulas. Let’s first start with a point in spherical coordinates and ask what the cylindrical coordinates of the point are. So, we know \(\left( {\rho ,\theta ,\varphi } \right)\) and want to find \(\left( {r,\theta ,z} \right)\). Of course, we really only need to find \(r\) and \(z\) since \(\theta \) is the same in both coordinate systems.
If we look at the sketch above from directly in front of the triangle we get the following sketch,
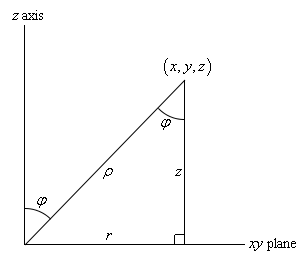
We know that the angle between the \(z\)-axis and \(\rho \) is \(\varphi \) and with a little geometry we also know that the angle between \(\rho \) and the vertical side of the right triangle is also \(\varphi \).
Then, with a little right triangle trig we get,
\[\begin{align*}z & = \rho \cos \varphi \\ r & = \rho \sin \varphi \end{align*}\]and these are exactly the formulas that we were looking for. So, given a point in spherical coordinates the cylindrical coordinates of the point will be,
Note as well from the Pythagorean theorem we also get,
Next, let’s find the Cartesian coordinates of the same point. To do this we’ll start with the cylindrical conversion formulas from the previous section.
\[\begin{align*}x & = r\cos \theta \\ y & = r\sin \theta \\ z & = z\end{align*}\]Now all that we need to do is use the formulas from above for \(r\) and \(z\) to get,
Also note that since we know that \({r^2} = {x^2} + {y^2}\) we get,
Converting points from Cartesian or cylindrical coordinates into spherical coordinates is usually done with the same conversion formulas. To see how this is done let’s work an example of each.
- Convert the point \(\displaystyle \left( {\sqrt 6 ,\frac{\pi }{4},\sqrt 2 } \right)\) from cylindrical to spherical coordinates.
- Convert the point \(\left( { - 1,1, - \sqrt 2 } \right)\) from Cartesian to spherical coordinates.
We’ll start by acknowledging that \(\theta \) is the same in both coordinate systems and so we don’t need to do anything with that.
Next, let’s find\(\rho \).
\[\rho = \sqrt {{r^2} + {z^2}} = \sqrt {6 + 2} = \sqrt 8 = 2\sqrt 2 \]Finally, let’s get \(\varphi \). To do this we can use either the conversion for \(r\) or \(z\). We’ll use the conversion for \(z\).
\[z = \rho \cos \varphi \hspace{0.25in} \Rightarrow \hspace{0.25in}\cos \varphi = \frac{z}{\rho } = \frac{{\sqrt 2 }}{{2\sqrt 2 }}\hspace{0.25in} \Rightarrow \hspace{0.25in}\varphi = {\cos ^{ - 1}}\left( {\frac{1}{2}} \right) = \frac{\pi }{3}\]Notice that there are many possible values of \(\varphi \) that will give \(\cos \varphi = \frac{1}{2}\), however, we have restricted \(\varphi \) to the range \(0 \le \varphi \le \pi \) and so this is the only possible value in that range.
So, the spherical coordinates of this point will are \(\left( {2\sqrt 2 ,\frac{\pi }{4},\frac{\pi }{3}} \right)\).
b Convert the point \(\left( { - 1,1, - \sqrt 2 } \right)\) from Cartesian to spherical coordinates. Show Solution
The first thing that we’ll do here is find \(\rho \).
\[\rho = \sqrt {{x^2} + {y^2} + {z^2}} = \sqrt {1 + 1 + 2} = 2\]Now we’ll need to find \(\varphi \). We can do this using the conversion for \(z\).
\[z = \rho \cos \varphi \hspace{0.25in} \Rightarrow \hspace{0.25in}\cos \varphi = \frac{z}{\rho } = \frac{{ - \sqrt 2 }}{2}\hspace{0.25in} \Rightarrow \hspace{0.25in}\varphi = {\cos ^{ - 1}}\left( {\frac{{ - \sqrt 2 }}{2}} \right) = \frac{{3\pi }}{4}\]As with the last parts this will be the only possible \(\varphi \) in the range allowed.
Finally, let’s find \(\theta \). To do this we can use the conversion for \(x\) or \(y\). We will use the conversion for \(y\) in this case.
\[\sin \theta = \frac{y}{{\rho \sin \varphi }} = \frac{1}{{2\left( {\frac{{\sqrt 2 }}{2}} \right)}} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\hspace{0.5in} \Rightarrow \hspace{0.25in}\theta = \frac{\pi }{4}\,\,{\mbox{or}}\,\,\theta = \frac{{3\pi }}{4}\]Now, we actually have more possible choices for \(\theta \) but all of them will reduce down to one of the two angles above since they will just be one of these two angles with one or more complete rotations around the unit circle added on.
We will however, need to decide which one is the correct angle since only one will be. To do this let’s notice that, in two dimensions, the point with coordinates \(x = - 1\) and \(y = 1\) lies in the second quadrant. This means that \(\theta \) must be angle that will put the point into the second quadrant. Therefore, the second angle, \(\theta = \frac{{3\pi }}{4}\), must be the correct one.
The spherical coordinates of this point are then \(\left( {2,\frac{{3\pi }}{4},\frac{{3\pi }}{4}} \right)\).
Now, let’s take a look at some equations and identify the surfaces that they represent.
- \(\rho = 5\)
- \(\displaystyle \varphi = \frac{\pi }{3}\)
- \(\displaystyle \theta = \frac{{2\pi }}{3}\)
- \(\rho \sin \varphi = 2\)
There are a couple of ways to think about this one.
First, think about what this equation is saying. This equation says that, no matter what \(\theta \) and \(\varphi \) are, the distance from the origin must be 5. So, we can rotate as much as we want away from the \(z\)-axis and around the \(z\)-axis, but we must always remain at a fixed distance from the origin. This is exactly what a sphere is. So, this is a sphere of radius 5 centered at the origin.
The other way to think about it is to just convert to Cartesian coordinates.
\[\begin{align*}\rho & = 5\\ {\rho ^2} & = 25\\ {x^2} + {y^2} + {z^2} & = 25\end{align*}\]Sure enough a sphere of radius 5 centered at the origin.
b \(\displaystyle \varphi = \frac{\pi }{3}\) Show Solution
In this case there isn’t an easy way to convert to Cartesian coordinates so we’ll just need to think about this one a little. This equation says that no matter how far away from the origin that we move and no matter how much we rotate around the \(z\)-axis the point must always be at an angle of \(\frac{\pi }{3}\) from the \(z\)-axis.
This is exactly what happens in a cone. All of the points on a cone are a fixed angle from the \(z\)-axis. So, we have a cone whose points are all at an angle of \(\frac{\pi }{3}\) from the \(z\)-axis.
c \(\displaystyle \theta = \frac{{2\pi }}{3}\) Show Solution
As with the last part we won’t be able to easily convert to Cartesian coordinates here. In this case no matter how far from the origin we get or how much we rotate down from the positive \(z\)-axis the points must always form an angle of \(\frac{{2\pi }}{3}\) with the \(x\)-axis.
Points in a vertical plane will do this. So, we have a vertical plane that forms an angle of \(\frac{{2\pi }}{3}\) with the positive \(x\)-axis.
d \(\rho \sin \varphi = 2\) Show Solution
In this case we can convert to Cartesian coordinates so let’s do that. There are actually two ways to do this conversion. We will look at both since both will be used on occasion.
Solution 1
In this solution method we will convert directly to Cartesian coordinates. To do this we will first need to square both sides of the equation.
Now, for no apparent reason add \({\rho ^2}{\cos ^2}\varphi \) to both sides.
\[\begin{align*}{\rho ^2}{\sin ^2}\varphi + {\rho ^2}{\cos ^2}\varphi & = 4 + {\rho ^2}{\cos ^2}\varphi \\ {\rho ^2}\left( {{{\sin }^2}\varphi + {{\cos }^2}\varphi } \right) & = 4 + {\rho ^2}{\cos ^2}\varphi \\ {\rho ^2} & = 4 + {\left( {\rho \cos \varphi } \right)^2}\end{align*}\]Now we can convert to Cartesian coordinates.
\[\begin{align*}{x^2} + {y^2} + {z^2} & = 4 + {z^2}\\ {x^2} + {y^2} & = 4\end{align*}\]So, we have a cylinder of radius 2 centered on the \(z\)-axis.
This solution method wasn’t too bad, but it did require some not so obvious steps to complete.
Solution 2
This method is much shorter, but also involves something that you may not see the first time around. In this case instead of going straight to Cartesian coordinates we’ll first convert to cylindrical coordinates.
This won’t always work, but in this case all we need to do is recognize that \(r = \rho \sin \varphi \) and we will get something we can recognize. Using this we get,
\[\begin{align*}\rho \sin \varphi & = 2\\ r & = 2\end{align*}\]At this point we know this is a cylinder (remember that we’re in three dimensions and so this isn’t a circle!). However, let’s go ahead and finish the conversion process out.
\[\begin{align*}{r^2} & = 4\\ {x^2} + {y^2} & = 4\end{align*}\]So, as we saw in the last part of the previous example it will sometimes be easier to convert equations in spherical coordinates into cylindrical coordinates before converting into Cartesian coordinates. This won’t always be easier, but it can make some of the conversions quicker and easier.
The last thing that we want to do in this section is generalize the first three parts of the previous example.
\[\begin{align*}\rho & = a\hspace{0.5in}{\mbox{sphere of radius }}a{\mbox{ centered at the origin}}\\ \varphi & = \alpha \hspace{0.5in}{\mbox{cone that makes an angle of }}\alpha {\mbox{ with the positive }}z - {\mbox{axis}}\\ \theta & = \beta \hspace{0.5in}{\mbox{vertical plane that makes an angle of }}\beta {\mbox{ with the positive }}x - {\mbox{axis}}\end{align*}\]