The next partial differential equation that we’re going to
solve is the 2-D Laplace’s equation,
A natural question to ask before we start learning how to
solve this is does this equation come up naturally anywhere? The answer is a very resounding yes! If we consider the 2-D heat equation,
We can see that
Laplace’s equation would correspond to finding the equilibrium solution (i.e. time independent solution) if there
were not sources. So, this is an
equation that can arise from physical situations.
How we solve Laplace’s equation will depend upon the
geometry of the 2-D object we’re solving it on.
Let’s start out by solving it on the rectangle given by 
,
. For this geometry Laplace’s equation along
with the four boundary conditions will be,
One of the important things to note here is that unlike the
heat equation we will not have any initial conditions here. Both variables are spatial variables and each
variable occurs in a 2nd order derivative and so we’ll need two
boundary conditions for each variable.
Next, let’s notice that while the partial differential
equation is both linear and homogeneous the boundary conditions are only linear
and are not homogeneous. This creates a problem
because separation of variables requires homogeneous boundary conditions.
To completely solve Laplace’s equation we’re in fact going
to have to solve it four times. Each
time we solve it only one of the four boundary conditions can be nonhomogeneous
while the remaining three will be homogeneous.
The four problems are probably best shown with a quick
sketch so let’s consider the following sketch.
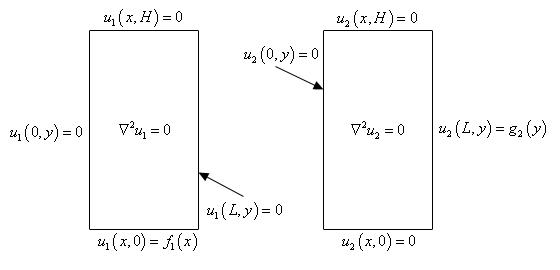
Now, once we solve all four of these problems the solution
to our original system, (1), will be,
Because we know that Laplace’s equation is linear and
homogeneous and each of the pieces is a solution to Laplace’s equation then the
sum will also be a solution. Also, this
will satisfy each of the four original boundary conditions. We’ll verify the first one and leave the rest
to you to verify.
In each of these cases the lone nonhomogeneous boundary condition
will take the place of the initial condition in the heat equation problems that
we solved a couple of sections ago. We
will apply separation of variables to the each problem and find a product
solution that will satisfy the differential equation and the three homogeneous
boundary conditions. Using the Principle
of Superposition we’ll find a solution to the problem and then apply the final
boundary condition to determine the value of the constant(s) that are left in
the problem. The process is nearly
identical in many ways to what we did when we were solving the heat equation.
We’re going to do two of the cases here and we’ll leave the
remaining two for you to do.
|
Example 1 Find
a solution to the following partial differential equation.
Solution
We’ll start by assuming that our solution will be in the
form,
and then recall
that we performed separation of variables on this problem (with a small
change in notation) back in Example 5 of the
Separation of Variables section. So
from that problem we know that separation of variables yields the following
two ordinary differential equations that we’ll need to solve.
Note that in
this case, unlike the heat equation we must solve the boundary value problem
first. Without knowing what is there is no way that we can solve
the first differential equation here with only one boundary condition since
the sign of will affect the solution.
Let’s also
notice that we solved the boundary value problem in Example 1 of Solving the
Heat Equation and so there is no reason to resolve it here. Taking a change of letters into account the
eigenvalues and eigenfunctions for the boundary value problem here are,
Now that we
know what the eigenvalues are let’s write down the first differential
equation with plugged in.
Because the
coefficient of in the differential equation above is
positive we know that a solution to this is,
However, this
is not really suited for dealing with the boundary condition. So, let’s also notice that the following is
also a solution.
You should
verify this by plugging this into the differential equation and checking that
it is in fact a solution. Applying the
lone boundary condition to this “shifted” solution gives,
The solution to
the first differential equation is now,
and this is all
the farther we can go with this because we only had a single boundary
condition. That is not really a
problem however because we now have enough information to form the product
solution for this partial differential equation.
A product
solution for this partial differential equation is,
The Principle
of Superposition then tells us that a solution to the partial differential
equation is,
and this
solution will satisfy the three homogeneous boundary conditions.
To determine
the constants all we need to do is apply the final boundary condition.
Now, in the
previous problems we’ve done this has clearly been a Fourier series of some
kind and in fact it still is. The
difference here is that the coefficients of the Fourier sine series are now,
instead of just
. We might be a little more tempted to use
the orthogonality of the sines to derive formulas for the ,
however we can still reuse the work that we’ve done previously to get
formulas for the coefficients here.
Remember that a
Fourier sine series is just a series of coefficients (depending on n) times a sine. We still have that here, except the
“coefficients” are a little messier this time that what we saw when we first
dealt with Fourier series. So, the
coefficients can be found using exactly the same formula from the Fourier sine series section of a function on
we just need to be careful with the
coefficients.
The formulas
for the are a little messy this time in comparison
to the other problems we’ve done but they aren’t really all that messy.
|
Okay, let’s do one of the other problems here so we can make
a couple of points.
|
Example 2 Find
a solution to the following partial differential equation.
Solution
Okay, for the first time we’ve hit a problem where we
haven’t previous done the separation of variables so let’s go through
that. We’ll assume the solution is in
the form,
We’ll apply
this to the homogeneous boundary conditions first since we’ll need those once
we get reach the point of choosing the separation constant. We’ll let you verify that the boundary
conditions become,
Next, we’ll
plug the product solution into the differential equation.
Now, at this
point we need to choose a separation constant. We’ve got two homogeneous boundary
conditions on h so let’s choose the
constant so that the differential equation for h yields a familiar boundary value problem so we don’t need to
redo any of that work. In this case,
unlike the case, we’ll need .
This is a good
problem in that is clearly illustrates that sometimes you need as a separation constant and at other times
you need . Not only that but sometimes all it takes is
a small change in the boundary conditions it force the change.
So, after
adding in the separation constant we get,
and two
ordinary differential equations that we get from this case (along with their
boundary conditions) are,
Now, as we
noted above when we were deciding which separation constant to work with
we’ve already solved the first boundary value problem. So, the eigenvalues and eigenfunctions for
the first boundary value problem are,
The second
differential equation is then,
Because the
coefficient of the is positive we know that a solution to this
is,
In this case,
unlike the previous example, we won’t need to use a shifted version of the
solution because this will work just fine with the boundary condition we’ve
got for this. So, applying the
boundary condition to this gives,
and this
solution becomes,
The product
solution for this case is then,
The solution to
this partial differential equation is then,
Finally, let’s apply the nonhomogeneous boundary condition
to get the coefficients for this solution.
As we’ve come
to expect this is again a Fourier sine (although it won’t always be a sine)
series and so using previously done work instead of using the orthogonality
of the sines to we see that,
|
Okay, we’ve worked two of the four cases that would need to
be solved in order to completely solve (1). As we’ve seen each case was very similar and
yet also had some differences. We saw
the use of both separation constants and that sometimes we need to use a
“shifted” solution in order to deal with one of the boundary conditions.
Before moving on let’s note that we used prescribed
temperature boundary conditions here, but we could just have easily used
prescribed flux boundary conditions or a mix of the two. No matter what kind of boundary conditions we
have they will work the same.
As a final example in this section let’s take a look at
solving Laplace’s equation on a disk of radius a and a prescribed temperature on the boundary. Because we are now on a disk it makes sense
that we should probably do this problem in polar coordinates and so the first
thing we need to so do is write down Laplace’s equation in terms of polar
coordinates.
Laplace’s equation in terms of polar coordinates is,
Okay, this is a lot more complicated than the Cartesian form
of Laplace’s equation and it will add in a few complexities to the solution
process, but it isn’t as bad as it looks.
The main problem that we’ve got here really is that fact that we’ve got
a single boundary condition. Namely,
This specifies the temperature on the boundary of the
disk. We are clearly going to need three
more conditions however since we’ve got a 2nd derivative in both r and .
When we solved Laplace’s equation on a rectangle we used
conditions at the end points of the range of each variable and so it makes some
sense here that we should probably need the same kind of conditions here as
well. The range on our variables here are,
Note that the limits on are somewhat arbitrary here and are chosen for
convenience here. Any set of limits that
covers the complete disk will work, however as we’ll see with these limits we
will get another familiar boundary value problem arising. The best choice here is often not known until
the separation of variables is done. At
that point you can go back and make your choices.
Okay, we now need conditions for and . First, note that Laplace’s equation in terms
of polar coordinates is singular at (i.e.
we get division by zero). However, we
know from physical considerations that the temperature must remain finite
everywhere in the disk and so let’s impose the condition that,
This may seem like an odd condition and it definitely
doesn’t conform to the other boundary conditions that we’ve seen to this point,
but it will work out for us as we’ll see.
Now, for boundary conditions for we’ll do something similar to what we did for
the 1-D head equation on a thin
ring. The two limits on are really just different sides of a line in
the disk and so let’s use the periodic conditions there. In other words,
With all of this out of the way let’s solve Laplace’s
equation on a disk of radius a.
|
Example 3 Find
a solution to the following partial differential equation.
Solution
In this case we’ll assume that the solution will be in the
form,
Plugging this
into the periodic boundary conditions gives,
Now let’s plug
the product solution into the partial differential equation.
This is
definitely more of a mess that we’ve seen to this point when it comes to
separating variables. In this case
simply dividing by the product solution, while still necessary, will not be
sufficient to separate the variables.
We are also going to have to multiply by to completely separate variables. So, doing all that, moving each term to one
side of the equal sign and introduction a separation constant gives,
We used as the separation constant this time to get
the differential equation for to match up with one we’ve already done.
The ordinary
differential equations we get are then,
Now, we solved
the boundary value problem above in Example
3 of the Eigenvalues and Eigenfunctions section of the previous chapter
and so there is no reason to redo it here.
The eigenvalues and eigenfunctions for this problem are,
Plugging this
into the first ordinary differential equation and using the product rule on
the derivative we get,
This is an Euler differential equation and so we know that
solutions will be in the form provided p
is a root of,
So, because the
case will yield a double root, versus two
real distinct roots if we have two cases here. They are,
Now we need to
recall the condition that . Each of the solutions above will have as Therefore in order to meet this boundary
condition we must have .
Therefore, the
solution reduces to,
and notice that
with the second term gone we can combine the two solutions into a single
solution.
So, we have two
product solutions for this problem.
They are,
Our solution is
then the sum of all these solutions or,
Applying our
final boundary condition to this gives,
This is a full Fourier
series for on the interval ,
i.e. . Also note that once again the
“coefficients” of the Fourier series are a little messier than normal, but
not quite as messy as when we were working on a rectangle above. We could once again use the orthogonality
of the sines and cosines to derive formulas for the and or we could just use the formulas from the Fourier series section with to get,
Upon solving
for the coefficients we get,
|
Prior to this example most of the separation of variable
problems tended to look very similar and it is easy to fall in to the trap of
expecting everything to look like what we’d seen earlier. With this example we can see that the
problems can definitely be different on occasion so don’t get too locked into
expecting them to always work in exactly the same way.
Before we leave this section let’s briefly talk about what
you’d need to do on a partial disk. The
periodic boundary conditions above were only there because we had a whole
disk. What if we only had a disk between
say .
When we’ve got a partial disk we now have two new boundaries
that we not present in the whole disk and the periodic boundary conditions will
no longer make sense. The periodic
boundary conditions are only used when we have the two “boundaries” in contact
with each other and that clearly won’t be the case with a partial disk.
So, if we stick with prescribed temperature boundary
conditions we would then have the following conditions
Also note that in order to use separation of variables on
these conditions we’d need to have to make sure they are homogeneous.
As a final note we could just have easily used flux boundary
conditions for the last two if we’d wanted to.
The boundary value problem would be different, but outside of that the
problem would work in the same manner.
We could also use a flux condition on the boundary but we haven’t really talked yet
about how to apply that kind of condition to our solution. Recall that this is the condition that we
apply to our solution to determine the coefficients. It’s not difficult to use we just haven’t
talked about this kind of condition yet.
We’ll be doing that in the next section.