Section 6.3 : Volume With Rings
In this section we will start looking at the volume of a solid of revolution. We should first define just what a solid of revolution is. To get a solid of revolution we start out with a function, \(y = f\left( x \right)\), on an interval \(\left[ {a,b} \right]\).

We then rotate this curve about a given axis to get the surface of the solid of revolution. For purposes of this discussion let’s rotate the curve about the \(x\)-axis, although it could be any vertical or horizontal axis. Doing this for the curve above gives the following three dimensional region.

What we want to do over the course of the next two sections is to determine the volume of this object.
In the Area and Volume Formulas section of the Extras chapter we derived the following formulas for the volume of this solid.
where, \(A\left( x \right)\) and \(A\left( y \right)\) are the cross-sectional area functions of the solid. There are many ways to get the cross-sectional area and we’ll see two (or three depending on how you look at it) over the next two sections. Whether we will use \(A\left( x \right)\) or \(A\left( y \right)\) will depend upon the method and the axis of rotation used for each problem.
One of the easier methods for getting the cross-sectional area is to cut the object perpendicular to the axis of rotation. Doing this the cross section will be either a solid disk if the object is solid (as our above example is) or a ring if we’ve hollowed out a portion of the solid (we will see this eventually).
In the case that we get a solid disk the area is,
\[A = \pi {\left( {{\mbox{radius}}} \right)^2}\]where the radius will depend upon the function and the axis of rotation.
In the case that we get a ring the area is,
where again both of the radii will depend on the functions given and the axis of rotation. Note as well that in the case of a solid disk we can think of the inner radius as zero and we’ll arrive at the correct formula for a solid disk and so this is a much more general formula to use.
Also, in both cases, whether the area is a function of \(x\) or a function of \(y\) will depend upon the axis of rotation as we will see.
This method is often called the method of disks or the method of rings.
Let’s do an example.
The first thing to do is get a sketch of the bounding region and the solid obtained by rotating the region about the \(x\)-axis. We don’t need a picture perfect sketch of the curves we just need something that will allow us to get a feel for what the bounded region looks like so we can get a quick sketch of the solid. With that in mind we can note that the first equation is just a parabola with vertex \(\left( {2,1} \right)\) (you do remember how to get the vertex of a parabola right?) and opens upward and so we don’t really need to put a lot of time into sketching it.
Here are both of these sketches.


Okay, to get a cross section we cut the solid at any \(x\). Below are a couple of sketches showing a typical cross section. The sketch on the right shows a cut away of the object with a typical cross section without the caps. The sketch on the left shows just the curve we’re rotating as well as its mirror image along the bottom of the solid.


In this case the radius is simply the distance from the \(x\)-axis to the curve and this is nothing more than the function value at that particular \(x\) as shown above. The cross-sectional area is then,
\[A\left( x \right) = \pi {\left( {{x^2} - 4x + 5} \right)^2} = \pi \left( {{x^4} - 8{x^3} + 26{x^2} - 40x + 25} \right)\]Next, we need to determine the limits of integration. Working from left to right the first cross section will occur at \(x = 1\) and the last cross section will occur at \(x = 4\). These are the limits of integration.
The volume of this solid is then,
\[\begin{align*}V &= \int_{{\,a}}^{{\,b}}{{A\left( x \right)\,dx}}\\ & = \pi \int_{{\,1}}^{{\,4}}{{{x^4} - 8{x^3} + 26{x^2} - 40x + 25\,dx}}\\ & = \pi \left. {\left( {\frac{1}{5}{x^5} - 2{x^4} + \frac{{26}}{3}{x^3} - 20{x^2} + 25x} \right)} \right|_1^4\\ & = \frac{{78\pi }}{5}\end{align*}\]In the above example the object was a solid object, but the more interesting objects are those that are not solid so let’s take a look at one of those.
First, let’s get a graph of the bounding region and a graph of the object. Remember that we only want the portion of the bounding region that lies in the first quadrant. There is a portion of the bounding region that is in the third quadrant as well, but we don't want that for this problem.
![This is the graphs of $y=\frac{x}{4}$ and $y=\sqrt[3]{x}$ (looks basically like the graph of $\sqrt{x}$) on the domain 0<x<8. This is the bounded region we are after for this example.](VolumeWithRings_Files/image007.gif)

There are a couple of things to note with this problem. First, we are only looking for the volume of the “walls” of this solid, not the complete interior as we did in the last example.
Next, we will get our cross section by cutting the object perpendicular to the axis of rotation. The cross section will be a ring (remember we are only looking at the walls) for this example and it will be horizontal at some \(y\). This means that the inner and outer radius for the ring will be \(x\) values and so we will need to rewrite our functions into the form \(x = f\left( y \right)\). Here are the functions written in the correct form for this example.
\[\begin{align*}y & = \sqrt[3]{x}\hspace{0.5in}\ \Rightarrow \hspace{0.5in}x = {y^3}\\ y & = \frac{x}{4}\hspace{0.65in} \Rightarrow \hspace{0.5in}x = 4y\end{align*}\]Here are a couple of sketches of the boundaries of the walls of this object as well as a typical ring. The sketch on the left includes the back portion of the object to give a little context to the figure on the right.


The inner radius in this case is the distance from the \(y\)-axis to the inner curve while the outer radius is the distance from the \(y\)-axis to the outer curve. Both of these are then \(x\) distances and so are given by the equations of the curves as shown above.
The cross-sectional area is then,
\[A\left( y \right) = \pi \left( {{{\left( {4y} \right)}^2} - {{\left( {{y^3}} \right)}^2}} \right) = \pi \left( {16{y^2} - {y^6}} \right)\]Working from the bottom of the solid to the top we can see that the first cross-section will occur at \(y = 0\) and the last cross-section will occur at \(y = 2\). These will be the limits of integration. The volume is then,
\[\begin{align*}V &= \int_{{\,c}}^{{\,d}}{{A\left( y \right)\,dy}}\\ & = \pi \int_{{\,0}}^{{\,2}}{{16{y^2} - {y^6}\,dy}}\\ & = \pi \left. {\left( {\frac{{16}}{3}{y^3} - \frac{1}{7}{y^7}} \right)} \right|_0^2\\ & = \frac{{512\pi }}{{21}}\end{align*}\]With these two examples out of the way we can now make a generalization about this method. If we rotate about a horizontal axis (the \(x\)-axis for example) then the cross-sectional area will be a function of \(x\). Likewise, if we rotate about a vertical axis (the \(y\)‑axis for example) then the cross-sectional area will be a function of \(y\).
The remaining two examples in this section will make sure that we don’t get too used to the idea of always rotating about the \(x\) or \(y\)-axis.
First let’s get the bounding region and the solid graphed.


Again, we are going to be looking for the volume of the walls of this object. Also, since we are rotating about a horizontal axis we know that the cross-sectional area will be a function of \(x\).
Here are a couple of sketches of the boundaries of the walls of this object as well as a typical ring. The sketch on the left includes the back portion of the object to give a little context to the figure on the right.


Now, we’re going to have to be careful here in determining the inner and outer radius as they aren’t going to be quite as simple they were in the previous two examples.
Let’s start with the inner radius as this one is a little clearer. First, the inner radius is NOT \(x\). The distance from the \(x\)-axis to the inner edge of the ring is \(x\), but we want the radius and that is the distance from the axis of rotation to the inner edge of the ring. So, we know that the distance from the axis of rotation to the \(x\)-axis is 4 and the distance from the \(x\)-axis to the inner ring is \(x\). The inner radius must then be the difference between these two. Or,
\[{\mbox{inner radius}} = 4 - x\]The outer radius works the same way. The outer radius is,
\[{\mbox{outer radius}} = 4 - \left( {{x^2} - 2x} \right) = - {x^2} + 2x + 4\]Note that given the location of the typical ring in the sketch above the formula for the outer radius may not look quite right but it is in fact correct. As sketched the outer edge of the ring is below the \(x\)-axis and at this point the value of the function will be negative and so when we do the subtraction in the formula for the outer radius we’ll actually be subtracting off a negative number which has the net effect of adding this distance onto 4 and that gives the correct outer radius. Likewise, if the outer edge is above the \(x\)-axis, the function value will be positive and so we’ll be doing an honest subtraction here and again we’ll get the correct radius in this case.
The cross-sectional area for this case is,
\[A\left( x \right) = \pi \left( {{{\left( { - {x^2} + 2x + 4} \right)}^2} - {{\left( {4 - x} \right)}^2}} \right) = \pi \left( {{x^4} - 4{x^3} - 5{x^2} + 24x} \right)\]The first ring will occur at \(x = 0\) and the last ring will occur at \(x = 3\) and so these are our limits of integration. The volume is then,
\[\begin{align*}V & = \int_{{\,a}}^{{\,b}}{{A\left( x \right)\,dx}}\\ & = \pi \int_{{\,0}}^{{\,3}}{{{x^4} - 4{x^3} - 5{x^2} + 24x\,dx}}\\ & = \pi \left. {\left( {\frac{1}{5}{x^5} - {x^4} - \frac{5}{3}{x^3} + 12{x^2}} \right)} \right|_0^3\\ & = \frac{{153\pi }}{5}\end{align*}\]As with the previous examples, let’s first graph the bounded region and the solid.

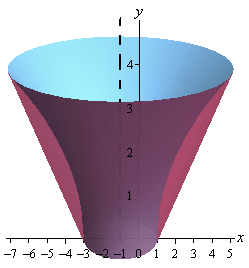
Now, let’s notice that since we are rotating about a vertical axis and so the cross-sectional area will be a function of \(y\). This also means that we are going to have to rewrite the functions to also get them in terms of \(y\).
\[\begin{align*}y &= 2\sqrt {x - 1} \hspace{0.5in} \Rightarrow \hspace{0.5in}x = \frac{{{y^2}}}{4} + 1\\ y & = x - 1\hspace{0.75in} \Rightarrow \hspace{0.5in}x = y + 1\end{align*}\]Here are a couple of sketches of the boundaries of the walls of this object as well as a typical ring. The sketch on the left includes the back portion of the object to give a little context to the figure on the right.
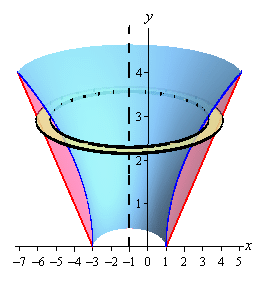

The inner and outer radius for this case is both similar and different from the previous example. This example is similar in the sense that the radii are not just the functions. In this example the functions are the distances from the \(y\)-axis to the edges of the rings. The center of the ring however is a distance of 1 from the \(y\)-axis. This means that the distance from the center to the edges is a distance from the axis of rotation to the \(y\)-axis (a distance of 1) and then from the \(y\)-axis to the edge of the rings.
So, the radii are then the functions plus 1 and that is what makes this example different from the previous example. Here we had to add the distance to the function value whereas in the previous example we needed to subtract the function from this distance. Note that without sketches the radii on these problems can be difficult to get.
So, in summary, we’ve got the following for the inner and outer radius for this example.
\[\begin{align*}{\mbox{outer radius}} & = y + 1 + 1 = y + 2\\ {\mbox{inner radius}} & = \frac{{{y^2}}}{4} + 1 + 1 = \frac{{{y^2}}}{4} + 2\end{align*}\]The cross-sectional area is then,
\[A\left( y \right) = \pi \left( {{{\left( {y + 2} \right)}^2} - {{\left( {\frac{{{y^2}}}{4} + 2} \right)}^2}} \right) = \pi \left( {4y - \frac{{{y^4}}}{{16}}} \right)\]The first ring will occur at \(y = 0\) and the final ring will occur at \(y = 4\) and so these will be our limits of integration.
The volume is,
\[\begin{align*}V & = \int_{{\,c}}^{{\,d}}{{A\left( y \right)\,dy}}\\ & = \pi \int_{{\,0}}^{{\,4}}{{4y - \frac{{{y^4}}}{{16}}\,dy}}\\ & = \pi \left. {\left( {2{y^2} - \frac{1}{{80}}{y^5}} \right)} \right|_0^4\\ & = \frac{{96\pi }}{5}\end{align*}\]