Section 3.4 : The Definition of a Function
18. Determine the domain of the following function.
\[f\left( x \right) = \frac{1}{{\sqrt {{x^2} - 8x + 15} }}\] Show SolutionRecall that the domain is simply all the values of \(x\) that we can plug into the function and the resulting function value will be a real number.
In this case we have a square root in the denominator of a rational expression. The numerator is a constant and so won’t cause any problems for us. However, because of the root in the denominator we need to require that the quantity under the root be positive.
Note as well that while we don’t have a problem with zero under a square root because the root is in the denominator allowing the quantity under the root to be zero would result in a division by zero problem and so we need to also avoid that.
In other words, we need to require,
\[\begin{align*}{x^2} - 8x + 15 & > 0\\ \left( {x - 3} \right)\left( {x - 5} \right) & > 0\end{align*}\]If you don’t recall how to solve polynomial inequalities you should go back to that section and do some of the practice problems there. Here is a quick solution for this one.
We can see that the polynomial on the left is zero at \(x = 3\) and \(x = 5\). A quick number line for this inequality is,
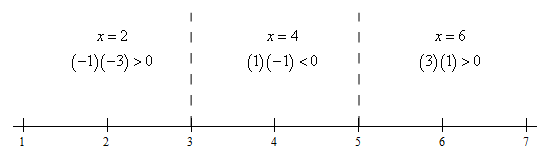
From this number line we can see that the polynomial is positive in the ranges \(x < 3\) and \(x > 5\) .
Therefore, the domain for this function is \(x < 3\) and \(x > 5\) .