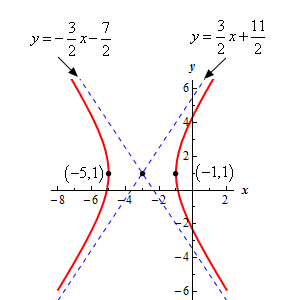I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.
Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.
Paul
February 18, 2026
Section 4.4 : Hyperbolas
2. Sketch the graph of the following hyperbola.
\[\frac{{{{\left( {x + 3} \right)}^2}}}{4} - \frac{{{{\left( {y - 1} \right)}^2}}}{9} = 1\]Show All Steps Hide All Steps
Start SolutionThe first step here is to simply compare our equation to the standard form of the hyperbola and identify all the important information. For reference purposes here is the standard form of the hyperbola that matches the one we have here.
\[\frac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} - \frac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1\]Comparing our equation to this we can see we have the following information.
\[h = - 3\hspace{0.25in}k = 1\hspace{0.25in}a = 2\hspace{0.25in}b = 3\]Because the \(x\) term is the positive term we know that this hyperbola will open right and left.
Show Step 2With the information we found in the first step we can see that the center of the hyperbola is \(\left( { - 3,1} \right)\).
The vertices of hyperbola are : \(\left( { - 5,1} \right)\) and \(\left( { - 1,1} \right)\).
The equations of the two asymptotes are,
\[y = 1 + \frac{3}{2}\left( {x + 3} \right) = \frac{3}{2}x + \frac{{11}}{2}\hspace{0.25in}y = 1 - \frac{3}{2}\left( {x + 3} \right) = - \frac{3}{2}x - \frac{7}{2}\] Show Step 3Here is a sketch of the hyperbola including the points and asymptotes we found above.