Section 2.3 : Applications of Linear Equations
4. Mike starts out 35 feet in front of Kim and they both start moving towards the right at the same time. Mike moves at 2 ft/sec while Kim moves at 3.4 ft/sec. How long will it take for Kim to catch up with Mike?
Show All Steps Hide All Steps
Start SolutionLet’s start with a diagram of what is going on in this situation.
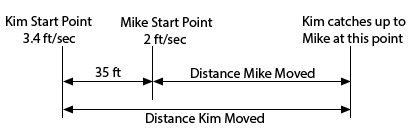
We can next set up a word equation for this situation.
\[\left( \begin{array}{c}{\mbox{Distance}}\\ {\mbox{Kim Moved}}\end{array} \right) = 35 + \left( \begin{array}{c}{\mbox{Distance}}\\ {\mbox{Mike Moved}}\end{array} \right)\]We know that Distance = Rate X Time so this gives to following word equation.
\[\left( \begin{array}{c}{\mbox{Rate of}}\\ {\mbox{Kim}}\end{array} \right)\left( \begin{array}{c}{\mbox{Time of}}\\ {\mbox{Kim}}\end{array} \right) = 35 + \left( \begin{array}{c}{\mbox{Rate of}}\\ {\mbox{Mike}}\end{array} \right)\left( \begin{array}{c}{\mbox{Time of}}\\ {\mbox{Mike}}\end{array} \right)\] Show Step 3Both Kim and Mike move for the same amount of time so let’s call that \(t\). We also know that Kim moves at 3.4 ft/sec while Mike moves at 2 ft/sec. Plugging all this information into the word equation above gives the following equation.
\[\begin{align*}\left( {3.4} \right)\left( t \right) & = 35 + \left( 2 \right)\left( t \right)\\ 3.4t & = 35 + 2t\end{align*}\] Show Step 4Now we can solve this equation for the time they traveled.
\[\begin{align*}3.4t & = 35 + 2t\\ 1.4t & = 35\\ t & = 25\end{align*}\]So, Kim will catch up with Mike after she moves for 25 seconds.