Next let’s set up a sketch for this situation.

Show Step 3

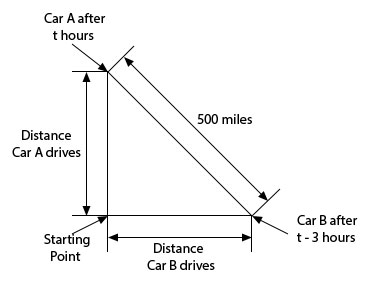
Okay. Now we need to get an equation for this situation. The first thing to notice about our sketch is that we have a right triangle! This means we can relate all three lengths using the Pythagorean Theorem (this is one of the reasons to have a sketch – to see these kinds of things).

The Pythagorean Theorem tells us that,

\[{\left( \begin{array}{c}{\mbox{Distance}}\\ {\mbox{Car A drives}}\end{array} \right)^2} + {\left( \begin{array}{c}{\mbox{Distance}}\\ {\mbox{Car B drives}}\end{array} \right)^2} = {\left( {500} \right)^2} = 250,000\] Show Step 4

Next, we know that we can find the distance of each car using the formula,

\[{\mbox{Distance}} = \left( {{\mbox{Speed of Car}}} \right)\left( {{\mbox{Time driving}}} \right)\]

So, for each car we have,

\[\begin{array}{l}{\mbox{Distance of Car A}} = \left( {40} \right)\left( t \right) = 40t\\ {\mbox{Distance of Car B}} = \left( {60} \right)\left( {t - 3} \right) = 60\left( {t - 3} \right)\end{array}\]

Putting all of this into the “word equation” we wrote down in Step 3 we get the following equation.

\[\begin{array}{rl}{\left( {40t} \right)^2} + {\left( {60\left( {t - 3} \right)} \right)^2} & = 250,000\\{40^2}{t^2} + {60^2}{\left( {t - 3} \right)^2} & = 250,000\\ 1600{t^2} + 3600\left( {{t^2} - 6t + 9} \right) & = 250,000\\ 1600{t^2} + 3600{t^2} - 21,600t + 32,400 & = 250,000\\5200{t^2} - 21,600t - 217,600 & = 0\end{array}\]

Note as well that we did quite a bit of simplification to get the equation into a standard form. Also, do not get excited about the “large” numbers here! They happen on occasion so they are nothing to worry about. This is still just a quadratic and we know how to solve quadratic equations. It doesn’t matter if the numbers are single digit numbers of significantly larger numbers as they are here.

Show Step 5

As noted in the previous step this is just a quadratic equation and we know how to solve those! Using the quadratic formula gives,

\[t = \frac{{ - \left( { - 21,600} \right) \pm \sqrt {{{\left( { - 21,600} \right)}^2} - 4\left( {5200} \right)\left( { - 217,600} \right)} }}{{2\left( {5200} \right)}} = \frac{{21,600 \pm \sqrt {4,992,640,000} }}{{10,400}}\] Show Step 6

Reducing the two values we got in the previous steps to decimals we arrive at the following two solutions to the quadratic equation from Step 4.

\[t = \frac{{21,600 - \sqrt {4,992,640,000} }}{{10,400}} = - 4.7172\hspace{0.25in}t = \frac{{21,600 + \sqrt {4,992,640,000} }}{{10,400}} = 8.8710\]

The first solution to the equation doesn’t make any sense since it is negative (we are working with time and so it’s safe to assume we are starting at \(t = 0\) after all!) so that means the second is the answer we need.

This means that Car A (i.e. the one traveling at 40 mph) travels for 8.871 hours while Car B (i.e. the one traveling at 60 mph) travels for 5.871 hours (three hours less than Car A time!).