Section 2.12 : Polynomial Inequalities
6. Solve the following inequality.
\[{t^4} + {t^3} - 12{t^2} < 0\]Show All Steps Hide All Steps
Start SolutionThe first thing we need to do is get a zero on one side of the inequality (which is already done for this problem) and then, if possible, factor the polynomial.
\[\begin{array}{c}{t^2}\left( {{t^2} + t - 12} \right) & < 0\\ {t^2}\left( {t + 4} \right)\left( {t - 3} \right) & < 0\end{array}\]Despite the fact that this is an inequality we first need to know where the polynomial is zero. From the factored from we can quickly see that the polynomial will be zero at,
\[t = - 4\hspace{0.25in}t = 0\hspace{0.25in}t = 3\]Remember that these points are important because they are the only places where the polynomial on the left side of the inequality might change sign. Given that we want to know where the polynomial is negative knowing where the polynomial might change sign will help considerably with determining the answer we’re looking for.
Recall from the discussion in the notes for this section that because the points from the previous step are the only places where the polynomial might change sign we can quickly determine if the polynomial is positive/negative in the ranges between each of these points simply by plugging in “test points” from each region into the polynomial to check the sign.
So, let’s sketch a quick number line with the points where the polynomial is zero graphed on it. We’ll also show the test point computations on the number line as well. Here is the number line.
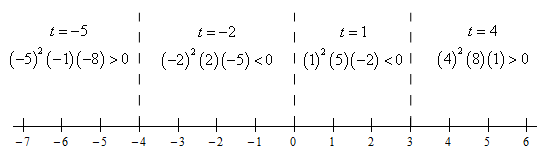
Be careful with the first term in the factored form when plugging in the test points! It is squared and so will always be positive regardless of the sign of the test points. One of the bigger mistakes that students make with this kind of problem is to miss the square and treat that term as negative when plugging in a negative test point.
Show Step 4All we need to do now is get the solution from the number line in the previous step. Here is both the inequality and interval notation from of the answer.
\[\require{bbox} \bbox[2pt,border:1px solid black]{\begin{array}{c} - 4 < t < 0\hspace{0.25in}{\mbox{and }}\hspace{0.25in}0 < t < 3\\ \left( { - 4,0} \right)\hspace{0.25in}{\mbox{and }}\hspace{0.25in}\left( {0,3} \right)\end{array}}\]Be careful with your answer here and don’t include \(t = 0\)! It might be tempting to do that to “simplify” the answer into a single inequality/interval but the polynomial is zero at \(t = 0\) and we only want to know where the polynomial is negative! Therefore we cannot include \(t = 0\) in our answer and we’ll need to write it as two inequalities/intervals.