Section 1.10 : Common Graphs
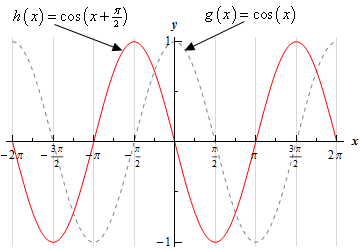
Without using a graphing calculator sketch the graph of \(h\left( x \right) = \cos \left( {x + \frac{\pi }{2}} \right)\).
Recall the basic Algebraic transformations. If we know the graph of \(g\left( x \right)\) then the graph of \(g\left( {x + c} \right)\) is simply the graph of \(g\left( x \right)\) shifted right by \(c\) units if \(c < 0\) or shifted left by \(c\) units if \(c > 0\).
So, in our case if \(g\left( x \right) = \cos \left( x \right)\) we can see that,
\[h\left( x \right) = \cos \left( {x + \frac{\pi }{2}} \right) = g\left( {x + \frac{\pi }{2}} \right)\]and so the graph we’re being asked to sketch is the graph of the cosine function shifted left by \(\frac{\pi }{2}\) units.
Here is the graph of \(h\left( x \right) = \cos \left( {x + \frac{\pi }{2}} \right)\) and note that to help see the transformation we have also sketched in the graph of \(g\left( x \right) = \cos \left( x \right)\).
