Calculus I - One-Sided Limits

Show Mobile Notice

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 2.3 : One-Sided Limits

Back to Problem List

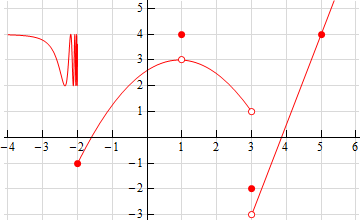
2. Below is the graph of $f\left( x \right)$ . For each of the given points determine the value of $f\left( a \right)$ , $\mathop {\lim }\limits_{x \to {a^{\, - }}} f\left( x \right)$ , $\mathop {\lim }\limits_{x \to {a^{\, + }}} f\left( x \right)$ , and $\mathop {\lim }\limits_{x \to a} f\left( x \right)$ . If any of the quantities do not exist clearly explain why.

$a = - 2$
$a = 1$
$a = 3$
$a = 5$

Show All Solutions Hide All Solutions

$a = - 2$ Show Solution

From the graph we can see that,

$\require{bbox} \bbox[2pt,border:1px solid black]{{f\left( { - 2} \right) = - 1}}$

because the closed dot is at the value of $y = - 1$ .

We can also see that as we approach $x = - 2$ from the left the graph is not approaching a single value, but instead oscillating wildly, and as we approach from the right the graph is approaching a value of -1. Therefore, we get,

$\require{bbox} \bbox[4pt,border:1px solid black]{{\mathop {\lim }\limits_{x \to \, - {2^{\, - }}} f\left( x \right){\mbox{ does not exist}}\hspace{0.25in} \& \hspace{0.25in},\mathop {\lim }\limits_{x \to \, - {2^{\, + }}} f\left( x \right) = - 1}}$

Recall that in order for limit to exist the function must be approaching a single value and so, in this case, because the graph to the left of $x = - 2$ is not approaching a single value the left-hand limit will not exist. This does not mean that the right-hand limit will not exist. In this case the graph to the right of $x = - 2$ is approaching a single value the right-hand limit will exist.

Now, because the two one-sided limits are different we know that,

$\require{bbox} \bbox[2pt,border:1px solid black]{{\mathop {\lim }\limits_{x \to \, - 2} f\left( x \right)\,\,{\mbox{does not exist}}}}$

$a = 1$ Show Solution

From the graph we can see that,

$\require{bbox} \bbox[2pt,border:1px solid black]{{f\left( 1 \right) = 4}}$

because the closed dot is at the value of $y = 4$ .

We can also see that as we approach $x = 1$ from both sides the graph is approaching the same value, 3, and so we get,

$\require{bbox} \bbox[4pt,border:1px solid black]{{\mathop {\lim }\limits_{x \to \,{1^{\, - }}} f\left( x \right) = 3\hspace{0.25in}\& \hspace{0.25in}\mathop {\lim }\limits_{x \to \,{1^{\, + }}} f\left( x \right) = 3}}$

The two one-sided limits are the same so we know,

$\require{bbox} \bbox[2pt,border:1px solid black]{{\mathop {\lim }\limits_{x \to \,1} f\left( x \right) = 3}}$

$a = 3$ Show Solution

From the graph we can see that,

$\require{bbox} \bbox[2pt,border:1px solid black]{{f\left( 3 \right) = - 2}}$

because the closed dot is at the value of $y = - 2$ .

We can also see that as we approach $x = 2$ from the left the graph is approaching a value of 1 and as we approach from the right the graph is approaching a value of -3. Therefore, we get,

$\require{bbox} \bbox[4pt,border:1px solid black]{{\mathop {\lim }\limits_{x \to \,{3^{\, - }}} f\left( x \right) = 1\hspace{0.25in}\& \hspace{0.25in}\mathop {\lim }\limits_{x \to \,{3^{\, + }}} f\left( x \right) = - 3}}$

Now, because the two one-sided limits are different we know that,

$\require{bbox} \bbox[2pt,border:1px solid black]{{\mathop {\lim }\limits_{x \to \,3} f\left( x \right)\,\,{\mbox{does not exist}}}}$

$a = 5$ Show Solution

From the graph we can see that,

$\require{bbox} \bbox[2pt,border:1px solid black]{{f\left( 5 \right) = 4}}$

because the closed dot is at the value of $y = 4$ .

We can also see that as we approach $x = 5$ from both sides the graph is approaching the same value, 4, and so we get,

$\require{bbox} \bbox[4pt,border:1px solid black]{{\mathop {\lim }\limits_{x \to \,{5^{\, - }}} f\left( x \right) = 4\hspace{0.25in}\& \hspace{0.25in}\mathop {\lim }\limits_{x \to \,{5^{\, + }}} f\left( x \right) = 4}}$

The two one-sided limits are the same so we know,

$\require{bbox} \bbox[2pt,border:1px solid black]{{\mathop {\lim }\limits_{x \to \,5} f\left( x \right) = 4}}$