Calculus II - Center of Mass

Show General Notice Show Mobile Notice Show All Notes Hide All Notes

General Notice

I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.

Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.

Paul
February 18, 2026

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 8.3 : Center Of Mass

Back to Problem List

3. Find the center of mass for the triangle with vertices \((0, 0)\), \((-4, 2)\) and \((0,6)\).

Show All Steps Hide All Steps

Start Solution

Let’s start out with a quick sketch of the region, with the center of mass indicated by the dot (the coordinates of this dot are of course to be determined in the final step…..).

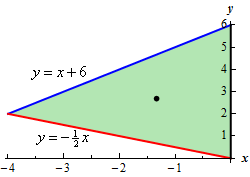
We’ll leave it to you verify the equations of the upper and lower leg of the triangle.

We’ll also need the area of this region so let’s find that first.

\[A = \int_{{ - 4}}^{0}{{\left( {x + 6} \right) - \left( { - \frac{1}{2}x} \right)\,dx}} = \int_{{ - 4}}^{0}{{\frac{3}{2}x + 6\,dx}} = \left. {\left( {\frac{3}{4}{x^2} + 6x} \right)} \right|_{ - 4}^0 = 12\] Show Step 2

Next, we need to compute the two moments. We didn’t include the density in the computations below because it will only cancel out in the final step.

\[\begin{align*}{M_x} & = \int_{{ - 4}}^{0}{{\frac{1}{2}\left[ {{{\left( {x + 6} \right)}^2} - {{\left( { - \frac{1}{2}x} \right)}^2}} \right]\,dx}} = \int_{{ - 4}}^{0}{{\frac{3}{8}{x^2} + 6x + 18\,dx}} = \left. {\left( {\frac{1}{8}{x^3} + 3{x^2} + 18x} \right)} \right|_{ - 4}^0 = 32\\ {M_y} & = \int_{{ - 4}}^{0}{{x\left( {\left( {x + 6} \right) - \left( { - \frac{1}{2}x} \right)} \right)\,dx}} = \int_{{ - 4}}^{0}{{\frac{3}{2}{x^2} + 6x\,dx}} = \left. {\left( {\frac{1}{2}{x^3} + 3{x^2}} \right)} \right|_{ - 4}^0 = - 16\end{align*}\] Show Step 3

Finally, the coordinates of the center of mass is,

\[\overline{x} = \frac{{{M_y}}}{M} = \frac{{\rho \left( { - 16} \right)}}{{\rho \left( {12} \right)}} = - \frac{4}{3}\hspace{0.25in}\hspace{0.25in}\overline{y} = \frac{{{M_x}}}{M} = \frac{{\rho \left( {32} \right)}}{{\rho \left( {12} \right)}} = \frac{8}{3}\]

The center of mass is then : \(\require{bbox} \bbox[2pt,border:1px solid black]{{\left( { - \frac{4}{3},\frac{8}{3}} \right)}}\).