Section 8.4 : Hydrostatic Pressure and Force
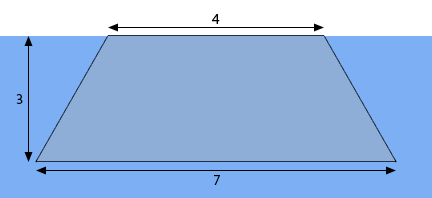
2. Find the hydrostatic force on the plate submerged in water as shown in the image below.
Consider the top of the blue “box” to be the surface of the water in which the plate is submerged. Note as well that the dimensions in the image will not be perfectly to scale in order to better fit the plate in the image. The lengths given in the image are in meters.
Show All Steps Hide All Steps
The first thing we should do is define an axis system for the portion of the plate that is below the water.

Note that we started the \(x\)-axis at the surface of the water and by doing this \(x\) will give the depth of any point on the plate below the surface of the water. This in turn means that the bottom of the plate will be defined by \(x = 3\).
It is always useful to define some kind of axis system for the plate to help with the rest of the problem. There are lots of ways to actually define the axis system and how we define them will in turn affect how we work the rest of the problem. There is nothing special about one definition over another but there is often an “easier” axis definition and by “easier’ we mean is liable to make some portions of the rest of the work go a little easier.
As we did in the notes we’ll break up the plate into \(n\) horizontal strips of width \(\Delta \,x\) and we’ll let each strip be defined by the interval \(\left[ {{x_{i - 1}},\,\,{x_i}} \right]\) with \(i = 1,2,3, \ldots n\). Finally, we’ll let \(x_i^*\) be any point that is in the interval and hence will be some point on the strip.
Below is yet another sketch of the plate only this time we’ve got a representative strip sketched on the plate. Note that the strip is “thicker” than the strip really should be but it will make it easier to see what the strip looks like and get all of the appropriate lengths clearly listed.
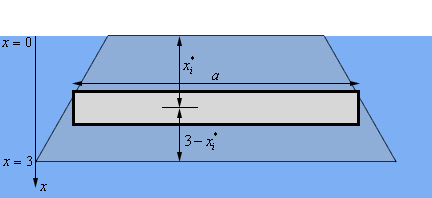
Now \(x_i^*\) is a point from the interval defining the strip and so, for sufficiently thin strips, it is safe to assume that the strip will be at the point \(x_i^*\) below the surface of the water as shown in the figure above. In other words, the strip is a distance of \(x_i^*\) below the surface of the water.
The width of each of the strips will be dependent on the depth of the strip and so temporarily let’s just call the width \(a\).
To determine the value of \(a\) for each strip let’s consider the following set of similar triangles.
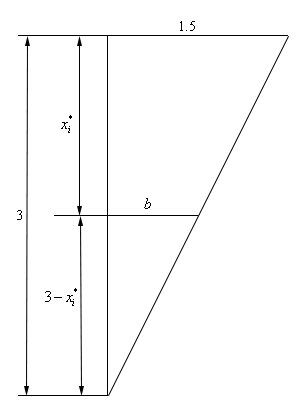
This is the triangle of “empty” space to the left of the plate. The overall height of the larger triangle is the same as the plate, namely 3. The overall width of the larger triangle is 1.5. We arrived at this number by noticing that the top of the plate was 3 meters shorter than the bottom and if we assume the top was perfectly centered over the bottom there must be 1.5 meters of “empty” space to either side of the top.
The top of the smaller triangle corresponds to the strip on the plate. We’ll call the width of the smaller triangle \(b\). and the height of the smaller triangle must be \(3 - x_i^*\) for each strip.
Because the two triangles are similar triangles we have the following equation.
\[\frac{b}{{3 - x_i^*}} = \frac{{1.5}}{3}\hspace{0.25in}\hspace{0.25in}b = \frac{1}{2}\left( {3 - x_i^*} \right)\]Note that while we looked only at the empty space to the left of the plate we’d get an almost identical triangle for the empty space to the right of the plate. The only exception would be that it would be a mirror image of this triangle.
Now, let’s get back to the width of the strip in our picture of the plate. Assuming that the top is centered over the bottom of the plate we can see that we have to have,
\[a = 7 - 2b = 7 - 2\left( {\frac{1}{2}} \right)\left( {3 - x_i^*} \right) = 4 + x_i^*\]We’ll assume that the strip is sufficiently thin so the hydrostatic pressure on the strip will be constant and is given by,
\[{P_i} = \rho g{d_i} = \left( {1000} \right)\left( {9.81} \right)x_i^* = 9810x_i^*\]This, in turn, means that the hydrostatic force on each strip is given by,
\[{F_i} = {P_i}{A_i} = \left( {9810x_i^*} \right)\left[ {\left( {4 + x_i^*} \right)\left( {\Delta \,x} \right)} \right] = 9810\left[ {4x_i^* + {{\left( {x_i^*} \right)}^2}} \right]\Delta \,x\]We can now approximate the total hydrostatic force on plate as the sum off the force on each of the strips. Or,
\[F \approx \sum\limits_{i = 1}^n {9810\left[ {4x_i^* + {{\left( {x_i^*} \right)}^2}} \right]\Delta \,x} \]Now, we can get an expression for the actual hydrostatic force on the plate simply by letting \(n\) go to infinity.
Or in other words, we take the limit as follows,
\[F = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {9810\left[ {4x_i^* + {{\left( {x_i^*} \right)}^2}} \right]\Delta \,x} \]Finally, we know from the definition of the definite integral that this is nothing more than the following definite integral that we can easily compute.
\[F = \int_{0}^{3}{{9810\left( {4x + {x^2}} \right)dx}} = \left. {9810\left( {2{x^2} + \frac{1}{3}{x^3}} \right)} \right|_0^3 = \require{bbox} \bbox[2pt,border:1px solid black]{{264,870N}}\]