From this we can see that the following substitution should work for us.

\[u = z + 1\hspace{0.5in} \Rightarrow \hspace{0.5in}du = dz\hspace{0.25in}\& \hspace{0.25in}z = u - 1\]

Doing the substitution gives,

\[\int{{\frac{{3z}}{{{{\left( {1 - 4z - 2{z^2}} \right)}^2}}}\,dz}} = \int{{\frac{{3\left( {u - 1} \right)}}{{{{\left( {3 - 2{u^2}} \right)}^2}}}\,du}} = \int{{\frac{{3u - 3}}{{{{\left( {3 - 2{u^2}} \right)}^2}}}\,du}}\] Show Step 3

Next, we’ll need to split the integral up as follows,

\[\int{{\frac{{3z}}{{{{\left( {1 - 4z - 2{z^2}} \right)}^2}}}\,dz}} = \int{{\frac{{3u}}{{{{\left( {3 - 2{u^2}} \right)}^2}}}\,du}} - \int{{\frac{3}{{{{\left( {3 - 2{u^2}} \right)}^2}}}\,du}}\]

The first integral can be done with the substitution \(v = 3 - 2{u^2}\) and the second integral will require the trig substitution \(u = \frac{{\sqrt 3 }}{{\sqrt 2 }}\sin \theta \) . Here is the substitution work.

\[\begin{align*}\int{{\frac{{3z}}{{{{\left( {1 - 4z - 2{z^2}} \right)}^2}}}\,dz}} & = - \frac{3}{4}\int{{{v^{ - 2}}\,dv}} - \int{{\frac{3}{{{{\left( {3 - 3{{\sin }^2}\theta } \right)}^2}}}\left( {\frac{{\sqrt 3 }}{{\sqrt 2 }}\cos \theta } \right)\,d\theta }}\\ & = - \frac{3}{4}\int{{{v^{ - 2}}\,dv}} - \int{{\frac{3}{{{{\left( {3{{\cos }^2}\theta } \right)}^2}}}\left( {\frac{{\sqrt 3 }}{{\sqrt 2 }}\cos \theta } \right)\,d\theta }}\\ & = - \frac{3}{4}\int{{{v^{ - 2}}\,dv}} - \frac{1}{{\sqrt 6 }}\int{{{{\sec }^3}\theta \,d\theta }}\end{align*}\]

The second integral for this problem comes down to an integral that was done in the notes for the second section of this chapter and so we’ll just use the formula derived in that section to do this integral.

Here is the rest of the integration process for this problem.

\[\int{{\frac{{3z}}{{{{\left( {1 - 4z - 2{z^2}} \right)}^2}}}\,dz}} = \frac{3}{4}{v^{ - 1}} - \frac{1}{{2\sqrt 6 }}\left[ {\sec \theta \tan \theta + \ln \left| {\sec \theta + \tan \theta } \right|} \right] + c\] Show Step 4

We now need to do quite a bit of back substitution to get the answer back into \(z\)’s. Let’s start with the result of the second integration. Converting the \(\theta \)’s back to \(u\)’s will require a quick right triangle.

From the substitution we have, \[\sin \theta = \frac{{\sqrt 2 \,u}}{{\sqrt 3 }}\,\,\,\,\,\left( { = \frac{{{\mbox{opp}}}}{{{\mbox{hyp}}}}} \right)\] From the right triangle we get, \[\tan \theta = \frac{{\sqrt 2 \,u}}{{\sqrt {3 - 2{u^2}} }}\,\,\,\,\,\,\,\& \,\,\,\,\,\,\,\sec \theta = \frac{{\sqrt 3 }}{{\sqrt {3 - 2{u^2}} }}\]

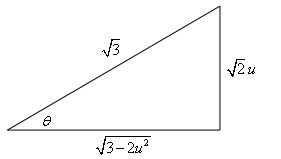
Plugging this into the integral above gives,

\[\int{{\frac{{3z}}{{{{\left( {1 - 4z - 2{z^2}} \right)}^2}}}\,dz}} = \frac{3}{{4\left( {3 - 2{u^2}} \right)}} - \frac{1}{{2\sqrt 6 }}\left[ {\frac{{\sqrt 6 \,u}}{{3 - 2{u^2}}} + \ln \left| {\frac{{\sqrt 3 + \sqrt 2 \,u}}{{\sqrt {3 - 2{u^2}} }}} \right|} \right] + c\]

Note that we also back substituted for the \(v\) in the first term as well and rewrote the first term a little. Finally, all we need to do is back substitute for the \(u\).

\[\int{{\frac{{3z}}{{{{\left( {1 - 4z - 2{z^2}} \right)}^2}}}\,dz}} = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{3}{{4\left( {3 - 2{{\left( {z + 1} \right)}^2}} \right)}} - \frac{{z + 1}}{{6 - 4{{\left( {z + 1} \right)}^2}}} - \frac{1}{{2\sqrt 6 }}\ln \left| {\frac{{\sqrt 3 + \sqrt 2 \,\left( {z + 1} \right)}}{{\sqrt {3 - 2{{\left( {z + 1} \right)}^2}} }}} \right| + c}}\]

We’ll leave this solution with a final note about these kinds of problems. They are often very long, messy and there are ample opportunities for mistakes so be careful with these and don’t get into too much of a hurry when working them.