Section 10.17 : Applications of Series
2. Write down \({T_2}\left( x \right)\), \({T_3}\left( x \right)\) and \({T_4}\left( x \right)\) for the Taylor Series of \(f\left( x \right) = {{\bf{e}}^{ - 6x}}\) about \(x = - 4\). Graph all three of the Taylor polynomials and \(f\left( x \right)\) on the same graph for the interval \(\left[ { - 8, - 2} \right]\).
Show All Steps Hide All Steps
Start SolutionThe first thing we need to do here is get the Taylor Series for \(f\left( x \right) = {{\bf{e}}^{ - 6x}}\) about \(x = - 4\). Luckily enough for us we did that in Problem 3 of the previous section. Here is the Taylor Series we derived in that problem.
\[{{\bf{e}}^{ - 6x}} = \sum\limits_{n = 0}^\infty {\frac{{{{\left( { - 6} \right)}^n}{{\bf{e}}^{24}}}}{{n!}}{{\left( {x + 4} \right)}^n}} \] Show Step 2Here are the three Taylor polynomials needed for this problem.
\[\begin{align*}{T_2}\left( x \right) & = {{\bf{e}}^{24}} - 6{{\bf{e}}^{24}}\left( {x + 4} \right) + 18{{\bf{e}}^{24}}{\left( {x + 4} \right)^2}\\ {T_3}\left( x \right) & = {{\bf{e}}^{24}} - 6{{\bf{e}}^{24}}\left( {x + 4} \right) + 18{{\bf{e}}^{24}}{\left( {x + 4} \right)^2} - 36{{\bf{e}}^{24}}{\left( {x + 4} \right)^3}\\ {T_4}\left( x \right) & = {{\bf{e}}^{24}} - 6{{\bf{e}}^{24}}\left( {x + 4} \right) + 18{{\bf{e}}^{24}}{\left( {x + 4} \right)^2} - 36{{\bf{e}}^{24}}{\left( {x + 4} \right)^3} + 54{{\bf{e}}^{24}}{\left( {x + 4} \right)^4}\end{align*}\] Show Step 3Here is the graph for this problem.
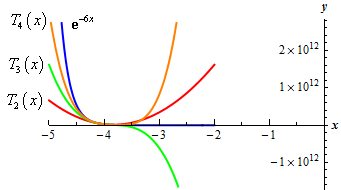
We can see that as long as we stay “near” \(x = - 4\) the graphs of the polynomial are pretty close to the graph of the exponential function. However, if we get too far away the graphs really do start to diverge from the graph of the exponential function.