I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.
Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.
Paul
February 18, 2026
Section 12.6 : Vector Functions
5. Sketch the graph of the vector function : \(\vec r\left( t \right) = \left\langle {4\sin \left( t \right),8\cos \left( t \right)} \right\rangle \)
Show All Steps Hide All Steps
Start SolutionOne way to sketch the graph of vector functions of course is to just compute a bunch of vectors and then recall that we consider them to be position vectors and plot the “points” we get out of them.
This will work provided we pick the “correct” values of \(t\) that gives us good points that we can use to actually determine what the graph is.
So, to avoid doing that, recall that because we consider these to be position vectors we can write down a corresponding set of parametric equations that we can use to sketch the graph. The parametric equations for this vector function are,
\[\begin{align*}x & = 4\sin \left( t \right)\\ y & = 8\cos \left( t \right)\end{align*}\] Show Step 2Now, recall from our look at parametric equations we now know that this will be the graph of an ellipse centered at the origin with right/left points a distance of 4 from the origin and top/bottom points a distance of 8 from the origin.
Show Step 3A sketch of the graph is below.
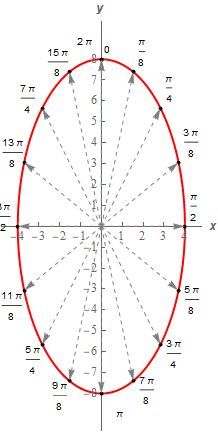
For illustration purposes we also put in a set of vectors for variety of \(t\)’s just to show that with enough them we would have also gotten the graph. Of course, it was easier to eliminate the parameter and just graph the algebraic equations (i.e. the equation involving only \(x\) and \(y\)).