I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.
Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.
Paul
February 18, 2026
Section 2.3 : Exact Equations
The next type of first order differential equations that we’ll be looking at is exact differential equations. Before we get into the full details behind solving exact differential equations it’s probably best to work an example that will help to show us just what an exact differential equation is. It will also show some of the behind the scenes details that we usually don’t bother with in the solution process.
The vast majority of the following example will not be done in any of the remaining examples and the work that we will put into the remaining examples will not be shown in this example. The whole point behind this example is to show you just what an exact differential equation is, how we use this fact to arrive at a solution and why the process works as it does. The majority of the actual solution details will be shown in a later example.
Let’s start off by supposing that somewhere out there in the world is a function \(\Psi\left(x,y\right)\) that we can find. For this example the function that we need is
\[\Psi \left( {x,y} \right) = {y^2} + \left( {{x^2} + 1} \right)y - 3{x^3}\]Do not worry at this point about where this function came from and how we found it. Finding the function, \(\Psi\left(x,y\right)\), that is needed for any particular differential equation is where the vast majority of the work for these problems lies. As stated earlier however, the point of this example is to show you why the solution process works rather than showing you the actual solution process. We will see how to find this function in the next example, so at this point do not worry about how to find it, simply accept that it can be found and that we’ve done that for this particular differential equation.
Now, take some partial derivatives of the function.
\[\begin{align*}{\Psi _x} & = 2xy - 9{x^2}\\ {\Psi _y} & = 2y + {x^2} + 1\end{align*}\]Now, compare these partial derivatives to the differential equation and you’ll notice that with these we can now write the differential equation as.
\[\begin{equation}{\Psi _x} + {\Psi _y}\frac{{dy}}{{dx}} = 0 \label{eq:eq1} \end{equation}\]Now, recall from your multi-variable calculus class (probably Calculus III), that \(\eqref{eq:eq1}\) is nothing more than the following derivative (you’ll need the multi-variable chain rule for this…).
\[\frac{d}{{dx}}\left( {\Psi \left( {x,y\left( x \right)} \right)} \right)\]So, the differential equation can now be written as
\[\frac{d}{{dx}}\left( {\Psi \left( {x,y\left( x \right)} \right)} \right) = 0\]Now, if the ordinary (not partial…) derivative of something is zero, that something must have been a constant to start with. In other words, we’ve got to have \(\Psi \left( {x,y} \right) = c\). Or,
\[{y^2} + \left( {{x^2} + 1} \right)y - 3{x^3} = c\]This then is an implicit solution for our differential equation! If we had an initial condition we could solve for \(c\). We could also find an explicit solution if we wanted to, but we’ll hold off on that until the next example.
Okay, so what did we learn from the last example? Let’s look at things a little more generally. Suppose that we have the following differential equation.
\[\begin{equation} M\left( {x,y} \right) + N\left( {x,y} \right)\frac{{dy}}{{dx}} = 0 \label{eq:eq2} \end{equation} \]Note that it’s important that it must be in this form! There must be an “= 0” on one side and the sign separating the two terms must be a “+”. Now, if there is a function somewhere out there in the world, \(\Psi\left(x,y\right)\), so that,
\[{\Psi _x} = M\left( {x,y} \right)\hspace{0.25in}\,\,\,\,\,\,\,\,\,\,\,\,{\mbox{and }}\,\,\hspace{0.25in}{\Psi _y} = N\left( {x,y} \right)\]then we call the differential equation exact. In these cases we can write the differential equation as
\[\begin{equation} {\Psi _x} + {\Psi _y}\frac{{dy}}{{dx}} = 0 \label{eq:eq3} \end{equation} \]Then using the chain rule from your Multivariable Calculus class we can further reduce the differential equation to the following derivative,
\[\frac{d}{{dx}}\left( {\Psi \left( {x,y\left( x \right)} \right)} \right) = 0\]The (implicit) solution to an exact differential equation is then
\[\begin{equation} \Psi \left( {x,y} \right) = c \label{eq:eq4} \end{equation} \]Well, it’s the solution provided we can find \(\Psi\left(x,y\right)\) anyway. Therefore, once we have the function we can always just jump straight to \(\eqref{eq:eq4}\) to get an implicit solution to our differential equation.
Finding the function \(\Psi\left(x,y\right)\) is clearly the central task in determining if a differential equation is exact and in finding its solution. As we will see, finding \(\Psi\left(x,y\right)\) can be a somewhat lengthy process in which there is the chance of mistakes. Therefore, it would be nice if there was some simple test that we could use before even starting to see if a differential equation is exact or not. This will be especially useful if it turns out that the differential equation is not exact, since in this case \(\Psi\left(x,y\right)\) will not exist. It would be a waste of time to try and find a nonexistent function!
So, let's see if we can find a test for exact differential equations. Let's start with \(\eqref{eq:eq2}\) and assume that the differential equation is in fact exact. Since its exact we know that somewhere out there is a function \(\Psi\left(x,y\right)\) that satisfies
\[\begin{align*}{\Psi _x} & = M\\ {\Psi _y} & = N\end{align*}\]Now, provided \(\Psi\left(x,y\right)\) is continuous and its first order derivatives are also continuous we know that
\[{\Psi _{x\,y}} = {\Psi _{y\,x}}\]However, we also have the following.
\[\begin{align*}{\Psi _{x\,y}} & = {\left( {{\Psi _x}} \right)_y} = {\left( M \right)_y} = {M_y}\\ {\Psi _{y\,x}} & = {\left( {{\Psi _y}} \right)_x} = {\left( N \right)_x} = {N_x}\end{align*}\]Therefore, if a differential equation is exact and \(\Psi\left(x,y\right)\) meets all of its continuity conditions we must have.
\[\begin{equation} {M_y} = {N_x} \label{eq:eq5} \end{equation}\]Likewise, if \(\eqref{eq:eq5}\) is not true there is no way for the differential equation to be exact.
Therefore, we will use \(\eqref{eq:eq5}\) as a test for exact differential equations. If \(\eqref{eq:eq5}\) is true we will assume that the differential equation is exact and that \(\Psi\left(x,y\right)\) meets all of its continuity conditions and proceed with finding it. Note that for all the examples here the continuity conditions will be met and so this won’t be an issue.
Okay, let’s go back and rework the first example. This time we will use the example to show how to find \(\Psi\left(x,y\right)\). We’ll also add in an initial condition to the problem.
First identify \(M\) and \(N\) and check that the differential equation is exact.
\[\begin{align*}M & = 2xy - 9{x^2}\hspace{0.25in}{M_y} = 2x\\ N & = 2y + {x^2} + 1\hspace{0.25in}{N_x} = 2x\end{align*}\]So, the differential equation is exact according to the test. However, we already knew that as we have given you \(\Psi\left(x,y\right)\). It’s not a bad thing to verify it however and to run through the test at least once however.
Now, how do we actually find \(\Psi\left(x,y\right)\)? Well recall that
\[\begin{align*}{\Psi _x} & = M\\ {\Psi _y} & = N\end{align*}\]We can use either of these to get a start on finding \(\Psi\left(x,y\right)\) by integrating as follows.
\[\Psi = \int{{M\,dx}}\hspace{0.25in}{\mbox{OR}}\hspace{0.25in}\Psi = \int{{N\,dy}}\]However, we will need to be careful as this won’t give us the exact function that we need. Often it doesn’t matter which one you choose to work with while in other problems one will be significantly easier than the other. In this case it doesn’t matter which one we use as either will be just as easy.
So, we’ll use the first one.
\[\Psi \left( {x,y} \right) = \int{{2xy - 9{x^2}\,dx}} = {x^2}y - 3{x^3} + h\left( y \right)\]Note that in this case the “constant” of integration is not really a constant at all, but instead it will be a function of the remaining variable(s), \(y\) in this case.
Recall that in integration we are asking what function we differentiated to get the function we are integrating. Since we are working with two variables here and talking about partial differentiation with respect to \(x\), this means that any term that contained only constants or \(y\)’s would have differentiated away to zero, therefore we need to acknowledge that fact by adding on a function of \(y\) instead of the standard \(c\).
Okay, we’ve got most of \(\Psi\left(x,y\right)\) we just need to determine \(h(y)\) and we’ll be done. This is actually easy to do. We used \({\Psi _x} = M\) to find most of \(\Psi\left(x,y\right)\) so we’ll use \({\Psi _y} = N\) to find \(h(y)\). Differentiate our \(\Psi\left(x,y\right)\) with respect to \(y\) and set this equal to \(N\) (since they must be equal after all). Don’t forget to “differentiate” \(h(y)\)! Doing this gives,
\[{\Psi _y} = {x^2} + h'\left( y \right) = 2y + {x^2} + 1 = N\]From this we can see that
\[h'\left( y \right) = 2y + 1\]Note that at this stage \(h(y)\) must be only a function of \(y\) and so if there are any \(x\)’s in the equation at this stage we have made a mistake somewhere and it’s time to go look for it.
We can now find \(h(y)\) by integrating.
\[h\left( y \right) = \int{{2y + 1\,dy}} = {y^2} + y + k\]You’ll note that we included the constant of integration, \(k\), here. It will turn out however that this will end up getting absorbed into another constant so we can drop it in general.
So, we can now write down \(\Psi\left(x,y\right)\).
\[\Psi \left( {x,y} \right) = {x^2}y - 3{x^3} + {y^2} + y + k = {y^2} + \left( {{x^2} + 1} \right)y - 3{x^3} + k\]With the exception of the \(k\) this is identical to the function that we used in the first example. We can now go straight to the implicit solution using \(\eqref{eq:eq4}\).
\[{y^2} + \left( {{x^2} + 1} \right)y - 3{x^3} + k = c\]We’ll now take care of the \(k\). Since both \(k\) and \(c\) are unknown constants all we need to do is subtract one from both sides and combine and we still have an unknown constant.
\[\begin{align*}{y^2} + \left( {{x^2} + 1} \right)y - 3{x^3} & = c - k\\ {y^2} + \left( {{x^2} + 1} \right)y - 3{x^3} & = c\end{align*}\]Therefore, we’ll not include the \(k\) in anymore problems.
This is where we left off in the first example. Let’s now apply the initial condition to find \(c\).
\[{\left( { - 3} \right)^2} + \left( {0 + 1} \right)\left( { - 3} \right) - 3{\left( 0 \right)^3} = c\hspace{0.25in} \Rightarrow \hspace{0.25in}\,\,\,\,\,c = 6\]The implicit solution is then.
\[{y^2} + \left( {{x^2} + 1} \right)y - 3{x^3} - 6 = 0\]Now, as we saw in the separable differential equation section, this is quadratic in \(y\) and so we can solve for \(y(x)\) by using the quadratic formula.
\[\begin{align*}y\left( x \right) & = \frac{{ - \left( {{x^2} + 1} \right) \pm \sqrt {{{\left( {{x^2} + 1} \right)}^2} - 4\left( 1 \right)\left( { - 3{x^3} - 6} \right)} }}{{2\left( 1 \right)}}\\ & = \frac{{ - \left( {{x^2} + 1} \right) \pm \sqrt {{x^4} + 12{x^3} + 2{x^2} + 25} }}{2}\end{align*}\]Now, reapply the initial condition to figure out which of the two signs in the \( \pm \) that we need.
\[ - 3 = y\left( 0 \right) = \frac{{ - 1 \pm \sqrt {25} }}{2} = \frac{{ - 1 \pm 5}}{2} = - 3,\,2\]So, it looks like the “-” is the one that we need. The explicit solution is then.
\[y\left( x \right) = \frac{{ - \left( {{x^2} + 1} \right) - \sqrt {{x^4} + 12{x^3} + 2{x^2} + 25} }}{2}\]Now, for the interval of validity. It looks like we might well have problems with square roots of negative numbers. So, we need to solve
\[{x^4} + 12{x^3} + 2{x^2} + 25 = 0\]Upon solving this equation is zero at \(x\) = –11.81557624 and \(x\) = –1.396911133. Note that you’ll need to use some form of computational aid in solving this equation. Here is a graph of the polynomial under the radical.
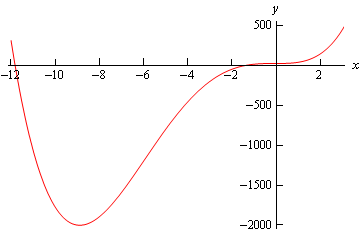
So, it looks like there are two intervals where the polynomial will be positive.
\[\begin{array}{c}- \infty < x \le - {\mbox{11}}{\mbox{.81557624}}\\ - {\mbox{1}}{\mbox{.396911133}} \le x < \infty \end{array}\]However, recall that intervals of validity need to be continuous intervals and contain the value of \(x\) that is used in the initial condition. Therefore, the interval of validity must be.
\[ - {\mbox{1}}{\mbox{.396911133}} \le x < \infty \]Here is a quick graph of the solution.
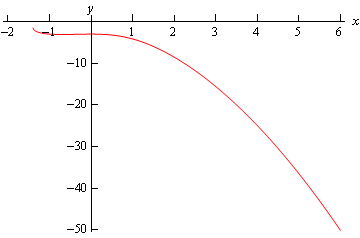
That was a long example, but mostly because of the initial explanation of how to find \(\Psi\left(x,y\right)\). The remaining examples will not be as long.
Here, we first need to put the differential equation into proper form before proceeding. Recall that it needs to be “= 0” and the sign separating the two terms must be a plus!
\[\begin{align*}2x{y^2} + 4 - 2\left( {3 - {x^2}y} \right)y' & = 0\\ 2x{y^2} + 4 + 2\left( {{x^2}y - 3} \right)y' & = 0\end{align*}\]So, we have the following
\[\begin{align*}M & = 2x{y^2} + 4\hspace{0.25in}{M_y} = 4xy\\ N & = 2{x^2}y - 6\hspace{0.25in}{N_x} = 4xy\end{align*}\]and so the differential equation is exact. We can either integrate \(M\) with respect to \(x\) or integrate \(N\) with respect to \(y\). In this case either would be just as easy so we’ll integrate \(N\) this time so we can say that we’ve got an example of both down here.
\[\Psi \left( {x,y} \right) = \int{{2{x^2}y - 6\,dy}} = {x^2}{y^2} - 6y + h\left( x \right)\]This time, as opposed to the previous example, our “constant” of integration must be a function of \(x\) since we integrated with respect to y. Now differentiate with respect to \(x\) and compare this to \(M\).
\[{\Psi _x} = 2x{y^2} + h'\left( x \right) = 2x{y^2} + 4 = M\]So, it looks like
\[h'\left( x \right) = 4\hspace{0.25in} \Rightarrow \hspace{0.25in}\,\,\,h\left( x \right) = 4x\]Again, we’ll drop the constant of integration that technically should be present in \(h(x)\) since it will just get absorbed into the constant we pick up in the next step. Also note that, \(h(x)\) should only involve \(x\)’s at this point. If there are any \(y\)’s left at this point a mistake has been made so go back and look for it.
Writing everything down gives us the following for \(\Psi\left(x,y\right)\).
\[\Psi \left( {x,y} \right) = {x^2}{y^2} - 6y + 4x\]So, the implicit solution to the differential equation is
\[{x^2}{y^2} - 6y + 4x = c\]Applying the initial condition gives,
\[64 - 48 - 4 = c\hspace{0.25in}c = 12\]The solution is then
\[{x^2}{y^2} - 6y + 4x - 12 = 0\]Using the quadratic formula gives us
\[\begin{align*}y\left( x \right) & = \frac{{6 \pm \sqrt {36 - 4{x^2}\left( {4x - 12} \right)} }}{{2{x^2}}}\\ & = \frac{{6 \pm \sqrt {36 + 48{x^2} - 16{x^3}} }}{{2{x^2}}}\\ & = \frac{{6 \pm 2\sqrt {9 + 12{x^2} - 4{x^3}} }}{{2{x^2}}}\\ & = \frac{{3 \pm \sqrt {9 + 12{x^2} - 4{x^3}} }}{{{x^2}}}\end{align*}\]Reapplying the initial condition shows that this time we need the “+” (we’ll leave those details to you to check). Therefore, the explicit solution is
\[y\left( x \right) = \frac{{3 + \sqrt {9 + 12{x^2} - 4{x^3}} }}{{{x^2}}}\]Now let’s find the interval of validity. We’ll need to avoid \(x\) = 0 so we don’t get division by zero. We’ll also have to watch out for square roots of negative numbers so solve the following equation.
\[ - 4{x^3} + 12{x^2} + 9 = 0\]The only real solution here is \(x = 3.217361577\). Below is a graph of the polynomial.
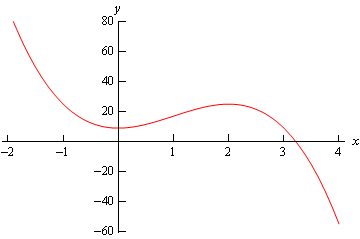
So, it looks like the polynomial will be positive, and hence okay under the square root on
\[ - \infty < x < {\mbox{3}}{\mbox{.217361577}}\]Now, this interval can’t be the interval of validity because it contains \(x = 0\) and we need to avoid that point. Therefore, this interval actually breaks up into two different possible intervals of validity.
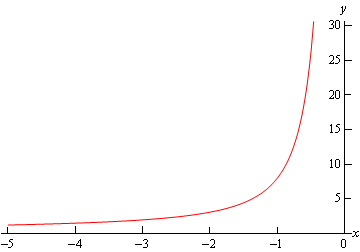
\[\begin{array}{c} - \infty < x < 0\\ 0 < x < {\mbox{3}}{\mbox{.217361577}}\end{array}\]The first one contains \(x = -1\), the \(x\) value from the initial condition. Therefore, the interval of validity for this problem is \( - \infty < x < 0\).
Here is a graph of the solution.
So, first deal with that minus sign separating the two terms.
\[\frac{{2ty}}{{{t^2} + 1}} - 2t + \left( {\ln \left( {{t^2} + 1} \right) - 2} \right)y' = 0\]Now, find \(M\) and \(N\) and check that it’s exact.
\[\begin{align*}M & = \frac{{2ty}}{{{t^2} + 1}} - 2t & \hspace{0.25in}{M_y} & = \frac{{2t}}{{{t^2} + 1}}\\ N & = \ln \left( {{t^2} + 1} \right) - 2 & \hspace{0.25in}{N_t} & = \frac{{2t}}{{{t^2} + 1}}\end{align*}\]So, it’s exact. We’ll integrate the first one in this case.
\[\Psi \left( {t,y} \right) = \int{{\frac{{2ty}}{{{t^2} + 1}} - 2t\,dt}} = y\ln \left( {{t^2} + 1} \right) - {t^2} + h\left( y \right)\]Differentiate with respect to \(y\) and compare to \(N\).
\[{\Psi _y} = \ln \left( {{t^2} + 1} \right) + h'\left( y \right) = \ln \left( {{t^2} + 1} \right) - 2 = N\]So, it looks like we’ve got.
\[h'\left( y \right) = - 2\hspace{0.25in}\,\, \Rightarrow \hspace{0.25in}\,\,\,h\left( y \right) = - 2y\]This gives us
\[\Psi \left( {t,y} \right) = y\ln \left( {{t^2} + 1} \right) - {t^2} - 2y\]The implicit solution is then,
\[y\ln \left( {{t^2} + 1} \right) - {t^2} - 2y = c\]Applying the initial condition gives,
\[ - 25 = c\]The implicit solution is now,
\[y\left( {\ln \left( {{t^2} + 1} \right) - 2} \right) - {t^2} = - 25\]This solution is much easier to solve than the previous ones. No quadratic formula is needed this time, all we need to do is solve for \(y\). Here’s what we get for an explicit solution.
\[y\left( t \right) = \frac{{{t^2} - 25}}{{\ln \left( {{t^2} + 1} \right) - 2}}\]Alright, let’s get the interval of validity. The term in the logarithm is always positive so we don’t need to worry about negative numbers in that. We do need to worry about division by zero however. We will need to avoid the following point(s).
\[\begin{align*}\ln \left( {{t^2} + 1} \right) - 2 & = 0\\ \ln \left( {{t^2} + 1} \right) & = 2\\ {t^2} + 1 & = {{\bf{e}}^2}\\ t & = \pm \sqrt {{{\bf{e}}^2} - 1} \end{align*}\]We now have three possible intervals of validity.
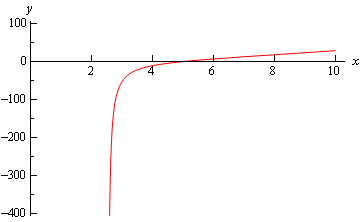
\[\begin{array}{ccc} - \infty < t < - \sqrt {{{\bf{e}}^2} - 1} \\ - \sqrt {{{\bf{e}}^2} - 1} < t < \sqrt {{{\bf{e}}^2} - 1} \\ \sqrt {{{\bf{e}}^2} - 1} < t < \infty \end{array}\]The last one contains \(t = 5\) and so is the interval of validity for this problem is \(\sqrt {{{\bf{e}}^2} - 1} < t < \infty \). Here’s a graph of the solution.
Let’s identify \(M\) and \(N\) and check that it’s exact.
\[\begin{align*}M & = 3{y^3}{{\bf{e}}^{3xy}} - 1 & \hspace{0.25in}{M_y} & = 9{y^2}{{\bf{e}}^{3xy}} + 9x{y^3}{{\bf{e}}^{3xy}}\\ N & = 2y{{\bf{e}}^{3xy}} + 3x{y^2}{{\bf{e}}^{3xy}} & \hspace{0.25in}{N_x} & = 9{y^2}{{\bf{e}}^{3xy}} + 9x{y^3}{{\bf{e}}^{3xy}}\end{align*}\]So, it’s exact. With the proper simplification integrating the second one isn’t too bad.
However, the first is already set up for easy integration so let’s do that one.
\[\Psi \left( {x,y} \right) = \int{{3{y^3}{{\bf{e}}^{3xy}} - 1\,dx}} = {y^2}{{\bf{e}}^{3xy}} - x + h\left( y \right)\]Differentiate with respect to \(y\) and compare to \(N\).
\[{\Psi _y} = 2y{{\bf{e}}^{3xy}} + 3x{y^2}{{\bf{e}}^{3xy}} + h'\left( y \right) = 2y{{\bf{e}}^{3xy}} + 3x{y^2}{{\bf{e}}^{3xy}} = N\]So, it looks like we’ve got
\[h'\left( y \right) = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}h\left( y \right) = 0\]Recall that actually \(h(y) = k\), but we drop the \(k\) because it will get absorbed in the next step. That gives us \(h(y) = 0\). Therefore, we get.
\[\Psi \left( {x,y} \right) = {y^2}{{\bf{e}}^{3xy}} - x\]The implicit solution is then
\[{y^2}{{\bf{e}}^{3xy}} - x = c\]Apply the initial condition.
\[1 = c\]The implicit solution is then
\[{y^2}{{\bf{e}}^{3xy}} - x = 1\]This is as far as we can go. There is no way to solve this for \(y\) and get an explicit solution.