I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.
Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.
Paul
February 18, 2026
Section 3.11 : Mechanical Vibrations
It’s now time to take a look at an application of second order differential equations. We’re going to take a look at mechanical vibrations. In particular we are going to look at a mass that is hanging from a spring.
Vibrations can occur in pretty much all branches of engineering and so what we’re going to be doing here can be easily adapted to other situations, usually with just a change in notation.
Let’s get the situation setup. We are going to start with a spring of length \(l\), called the natural length, and we’re going to hook an object with mass \(m\) up to it. When the object is attached to the spring the spring will stretch a length of \(L\). We will call the equilibrium position the position of the center of gravity for the object as it hangs on the spring with no movement.
Below is sketch of the spring with and without the object attached to it.
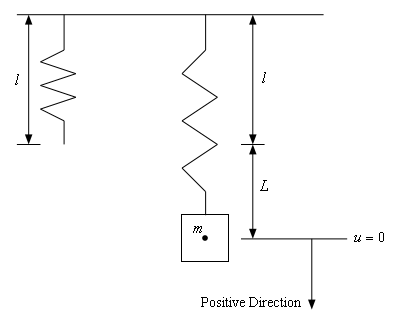
As denoted in the sketch we are going to assume that all forces, velocities, and displacements in the downward direction will be positive. All forces, velocities, and displacements in the upward direction will be negative.
Also, as shown in the sketch above, we will measure all displacement of the mass from its equilibrium position. Therefore, the \(u = 0\) position will correspond to the center of gravity for the mass as it hangs on the spring and is at rest (i.e. no movement).
Now, we need to develop a differential equation that will give the displacement of the object at any time \(t\). First, recall Newton’s Second Law of Motion.
\[ma = F\]In this case we will use the second derivative of the displacement, \(u\), for the acceleration and so Newton<’s Second Law becomes,
\[mu'' = F\left( {t,u,u'} \right)\]We now need to determine all the forces that will act upon the object. There are four forces that we will assume act upon the object. Two that will always act on the object and two that may or may not act upon the object.
Here is a list of the forces that will act upon the object.
- Gravity, \(F_{g}\)
The force due to gravity will always act upon the object of course. This force is
\[{F_g} = mg\] - Spring, \(F_{s}\)
We are going to assume that Hooke’s Law will govern the force that the spring exerts on the object. This force will always be present as well and is
\[{F_s} = - k\left( {L + u} \right)\]Hooke’s Law tells us that the force exerted by a spring will be the spring constant, \(k > 0\), times the displacement of the spring from its natural length. For our set up the displacement from the spring’s natural length is \(L + u\) and the minus sign is in there to make sure that the force always has the correct direction.
Let’s make sure that this force does what we expect it to. If the object is at rest in its equilibrium position the displacement is \(L\) and the force is simply \(F_{s} = –kL\) which will act in the upward position as it should since the spring has been stretched from its natural length.
If the spring has been stretched further down from the equilibrium position then \(L + u\) will be positive and \(F_{s}\) will be negative acting to pull the object back up as it should be.
Next, if the object has been moved up past its equilibrium point, but not yet to its natural length then \(u\) will be negative, but still less than \(L\) and so \(L + u\) will be positive and once again \(F_{s}\) will be negative acting to pull the object up.
Finally, if the object has been moved upwards so that the spring is now compressed, then \(u\) will be negative and greater than \(L\). Therefore, \(L + u\) will be negative and now \(F_{s}\) will be positive acting to push the object down.
So, it looks like this force will act as we expect that it should.
- Damping, \(F_{d}\)
The next force that we need to consider is damping. This force may or may not be present for any given problem.
Dampers work to counteract any movement. There are several ways to define a damping force. The one that we’ll use is the following.
\[{F_d} = - \gamma \,u'\]where, \(\gamma > 0\) is the damping coefficient. Let’s think for a minute about how this force will act. If the object is moving downward, then the velocity (\(u'\)) will be positive and so \(F_{d}\) will be negative and acting to pull the object back up. Likewise, if the object is moving upward, the velocity (\(u'\)) will be negative and so \(F_{d}\) will be positive and acting to push the object back down.
In other words, the damping force as we’ve defined it will always act to counter the current motion of the object and so will act to damp out any motion in the object.
- External Forces, \(F(t)\)
This is the catch all force. If there are any other forces that we decide we want to act on our object we lump them in here and call it good. We typically call \(F(t)\) the forcing function.
Putting all of these together gives us the following for Newton’s Second Law.
\[mu'' = mg - k\left( {L + u} \right) - \gamma u' + F\left( t \right)\]Or, upon rewriting, we get,
\[mu'' + \gamma u' + ku = mg - kL + F\left( t \right)\]Now, when the object is at rest in its equilibrium position there are exactly two forces acting on the object, the force due to gravity and the force due to the spring. Also, since the object is at rest (i.e. not moving) these two forces must be canceling each other out. This means that we must have,
\[\begin{equation}mg = kL\label{eq:eq1}\end{equation}\]Using this in Newton’s Second Law gives us the final version of the differential equation that we’ll work with.
\[\begin{equation}mu'' + \gamma u' + ku = F\left( t \right)\label{eq:eq2}\end{equation}\]Along with this differential equation we will have the following initial conditions.
\[\begin{equation}\begin{aligned}u\left( 0 \right) & = {u_0}\hspace{0.25in}{\mbox{Initial displacement from the equilibrium position}}{\mbox{.}}\\ u'\left( 0 \right) & = {{u'}_0}\hspace{0.25in}{\mbox{Initial velocity}}{\mbox{.}}\end{aligned}\label{eq:eq3}\end{equation}\]Note that we’ll also be using \(\eqref{eq:eq1}\) to determine the spring constant, \(k\).
Okay. Let’s start looking at some specific cases.
Free, Undamped Vibrations
This is the simplest case that we can consider. Free or unforced vibrations means that \(F(t) = 0\) and undamped vibrations means that \(\gamma = 0\). In this case the differential equation becomes,
\[mu'' + ku = 0\]This is easy enough to solve in general. The characteristic equation has the roots,
\[r = \pm \,\,i\,\sqrt {\frac{k}{m}} \]This is usually reduced to,
\[r = \pm \,{\omega _0}\,i\]where,
\[\omega {_0} = \sqrt {\frac{k}{m}} \]and \({\omega _0}\) is called the natural frequency. Recall as well that \(m > 0\) and \(k > 0\) and so we can guarantee that this quantity will not be complex. The solution in this case is then
\[\begin{equation} u\left( t \right) = {c_1}\cos \left( {{\omega _0}\,t} \right) + {c_2}\sin \left( {{\omega _0}\,t} \right)\label{eq:eq4}\end{equation}\]We can write \(\eqref{eq:eq4}\) in the following form,
\[\begin{equation}u\left( t \right) = R\cos \left( {{\omega _0}t - \delta } \right)\label{eq:eq5}\end{equation}\]where \(R\) is the amplitude of the displacement and \(\delta \) is the phase shift or phase angle of the displacement.
When the displacement is in the form of \(\eqref{eq:eq5}\) it is usually easier to work with. However, it’s easier to find the constants in \(\eqref{eq:eq4}\) from the initial conditions than it is to find the amplitude and phase shift in \(\eqref{eq:eq5}\) from the initial conditions. So, in order to get the equation into the form in \(\eqref{eq:eq5}\) we will first put the equation in the form in \(\eqref{eq:eq4}\), find the constants, \(c_{1}\) and \(c_{2}\) and then convert this into the form in \(\eqref{eq:eq5}\).
So, assuming that we have \(c_{1}\) and \(c_{2}\) how do we determine \(R\) and \(\delta \)? Let’s start with \(\eqref{eq:eq5}\) and use a trig identity to write it as
\[\begin{equation}u\left( t \right) = R\cos \left( \delta \right)\cos \left( {{\omega _0}t} \right) + R\sin \left( \delta \right)\sin \left( {{\omega _0}t} \right)\label{eq:eq6}\end{equation}\]Now, \(R\) and \(\delta \) are constants and so if we compare \(\eqref{eq:eq6}\) to \(\eqref{eq:eq4}\) we can see that
\[{c_1} = R\cos \delta \hspace{0.25in}{c_2} = R\sin \delta \]We can find \(R\) in the following way.
\[c_1^2 + c_2^2 = {R^2}{\cos ^2}\delta + {R^2}{\sin ^2}\delta = {R^2}\]Taking the square root of both sides and assuming that \(R\) is positive will give
\[\begin{equation}R = \sqrt {c_1^2 + c_2^2} \label{eq:eq7}\end{equation}\]Finding \(\delta \) is just as easy. We’ll start with
\[\frac{{{c_2}}}{{{c_1}}} = \frac{{R\sin \delta }}{{R\cos \delta }} = \tan \delta \]Taking the inverse tangent of both sides gives,
\[\begin{equation}\delta = {\tan ^{ - 1}}\left( {\frac{{{c_2}}}{{{c_1}}}} \right)\label{eq:eq8}\end{equation}\]Before we work any examples let’s talk a little bit about units of mass and the Imperial vs. metric system differences.
Recall that the weight of the object is given by
\[W = mg\]where \(m\) is the mass of the object and \(g\) is the gravitational acceleration. For the examples in this problem we’ll be using the following values for \(g\).
\[\begin{align*}&{\mbox{Imperial : }}g = 32\,\,ft/{s^2}\\ & {\mbox{Metric : }}g = 9.8\,\,m/{s^2}\end{align*}\]This is not the standard 32.2 ft/s2 or 9.81 m/s2, but using these will make some of the numbers come out a little nicer.
In the metric system the mass of objects is given in kilograms (kg) and there is nothing for us to do. However, in the British system we tend to be given the weight of an object in pounds (yes, pounds are the units of weight not mass…) and so we’ll need to compute the mass for these problems.
At this point we should probably work an example of all this to see how this stuff works.
We first need to set up the IVP for the problem. This requires us to get our hands on \(m\) and \(k\).
This is the Imperial system so we’ll need to compute the mass.
\[m = \frac{W}{g} = \frac{{16}}{{32}} = \frac{1}{2}\]Now, let’s get \(k\). We can use the fact that \(mg = kL\) to find \(k\). Don’t forget that we’ll need all of our length units the same. We’ll use feet for the unit of measurement for this problem.
\[k = \frac{{mg}}{L} = \frac{{16}}{{{}^{8}/{}_{9}}} = 18\]We can now set up the IVP.
\[\frac{1}{2}u'' + 18u = 0\hspace{0.25in}u\left( 0 \right) = - \frac{1}{2}\hspace{0.25in}u'\left( 0 \right) = 1\]For the initial conditions recall that upward displacement/motion is negative while downward displacement/motion is positive. Also, since we decided to do everything in feet we had to convert the initial displacement to feet.
Now, to solve this we can either go through the characteristic equation or we can just jump straight to the formula that we derived above. We’ll do it that way. First, we need the natural frequency,
\[{\omega _0} = \sqrt {\frac{{18}}{{{}^{1}/{}_{2}}}} = \sqrt {36} = 6\]The general solution, along with its derivative, is then,
\[\begin{align*}u\left( t \right) & = {c_1}\cos \left( {6t} \right) + {c_2}\sin \left( {6t} \right)\\ u'\left( t \right) & = - 6{c_1}\sin \left( {6t} \right) + 6{c_2}\cos \left( {6t} \right)\end{align*}\]Applying the initial conditions gives
\[\begin{align*} - \frac{1}{2} = u\left( 0 \right) & = {c_1}\hspace{0.25in}{c_1} = - \frac{1}{2}\\ 1 = u'\left( 0 \right) & = 6{c_2}\cos \left( {6t} \right)\hspace{0.25in}{c_2} = \frac{1}{6}\end{align*}\]The displacement at any time \(t\) is then
\[u\left( t \right) = - \frac{1}{2}\cos \left( {6t} \right) + \frac{1}{6}\sin \left( {6t} \right)\]Now, let’s convert this to a single cosine. First let’s get the amplitude, \(R\).
\[R = \sqrt {{{\left( { - \frac{1}{2}} \right)}^2} + {{\left( {\frac{1}{6}} \right)}^2}} = \frac{{\sqrt {10} }}{6} = 0.52705\]You can use either the exact value here or a decimal approximation. Often the decimal approximation will be easier.
Now let’s get the phase shift.
\[\delta = {\tan ^{ - 1}}\left( {\frac{{{}^{1}/{}_{6}}}{{ - {}^{1}/{}_{2}}}} \right) = - 0.32175\]We need to be careful with this part. The phase angle found above is in Quadrant IV, but there is also an angle in Quadrant II that would work as well. We get this second angle by adding \(\pi \) onto the first angle. So, we actually have two angles. They are
\[\begin{align*}{\delta _1} & = - 0.32175\\ {\delta _2} & = {\delta _1} + \pi = 2.81984\end{align*}\]We need to decide which of these phase shifts is correct, because only one will be correct. To do this recall that
\[\begin{align*}{c_1} & = R\cos \delta \\ {c_2} & = R\sin \delta \end{align*}\]Now, since we are assuming that \(R\) is positive this means that the sign of \(\cos \delta \) will be the same as the sign of \(c_{1}\) and the sign of \(\sin \delta \) will be the same as the sign of \(c_{2}\). So, for this particular case we must have \(\cos \delta < 0\) and \(\sin \delta > 0\). This means that the phase shift must be in Quadrant II and so the second angle is the one that we need.
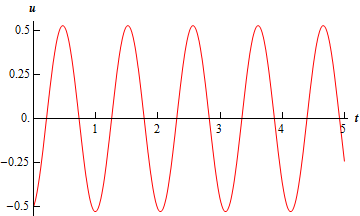
So, after all of this the displacement at any time \(t\) is.
\[u\left( t \right) = 0.52705\cos \left( {6t - 2.81984} \right)\]Here is a sketch of the displacement for the first 5 seconds.
Now, let’s take a look at a slightly more realistic situation. No vibration will go on forever. So, let’s add in a damper and see what happens now.
Free, Damped Vibrations
We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. In this case the differential equation will be.
\[mu'' + \gamma u' + ku = 0\]where \(m\), \(\gamma \), and \(k\) are all positive constants. Upon solving for the roots of the characteristic equation we get the following.
\[{r_{1,2}} = \frac{{ - \gamma \pm \sqrt {{\gamma ^2} - 4mk} }}{{2m}}\]We will have three cases here.
- \({\gamma ^2} - 4mk = 0\)
In this case we will get a double root out of the characteristic equation and the displacement at any time \(t\) will be.
\[u\left( t \right) = {c_1}{{\bf{e}}^{ - \frac{{\gamma \,t}}{{2\,m}}}} + {c_2}t{{\bf{e}}^{ - \frac{{\gamma \,t}}{{2\,m}}}}\]Notice that as \(t \to \infty \) the displacement will approach zero and so the damping in this case will do what it’s supposed to do.
This case is called critical damping and will happen when the damping coefficient is,
\[\begin{align*}{\gamma ^2} - 4mk & = 0\\ {\gamma ^2} & = 4mk\\ \gamma & = 2\sqrt {mk} = {\gamma _{CR}}\end{align*}\]The value of the damping coefficient that gives critical damping is called the critical damping coefficient and denoted by \({\gamma _{CR}}\).
- \({\gamma ^2} - 4mk > 0\)
In this case let’s rewrite the roots a little.
\[\begin{align*}{r_{1,2}} & = \frac{{ - \gamma \pm \sqrt {{\gamma ^2} - 4mk} }}{{2m}}\\ & = \frac{{ - \gamma \pm \gamma \sqrt {1 - \frac{{4mk}}{{{\gamma ^2}}}} }}{{2m}}\\ & = - \frac{\gamma }{{2m}}\left( {1 \pm \sqrt {1 - \frac{{4mk}}{{{\gamma ^2}}}} } \right)\end{align*}\]Also notice that from our initial assumption that we have,
\[\begin{align*}{\gamma ^2} & > 4mk\\ 1 & > \frac{{4mk}}{{{\gamma ^2}}}\end{align*}\]Using this we can see that the fraction under the square root above is less than one. Then if the quantity under the square root is less than one, this means that the square root of this quantity is also going to be less than one. In other words,
\[\sqrt {1 - \frac{{4mk}}{{{\gamma ^2}}}} < 1\]Why is this important? Well, the quantity in the parenthesis is now one plus/minus a number that is less than one. This means that the quantity in the parenthesis is guaranteed to be positive and so the two roots in this case are guaranteed to be negative. Therefore, the displacement at any time \(t\) is,
\[u\left( t \right) = {c_1}{{\bf{e}}^{{r_1}t}} + {c_2}{{\bf{e}}^{{r_2}t}}\]and will approach zero as \(t \to \infty \). So, once again the damper does what it is supposed to do.
This case will occur when
\[\begin{align*}{\gamma ^2} & > 4mk\\ \gamma & > 2\sqrt {mk} \\ \gamma & > {\gamma _{CR}}\end{align*}\]and is called over damping.
- \({\gamma ^2} - 4mk < 0\)
In this case we will get complex roots out of the characteristic equation.
\[{r_{1,2}} = \frac{{ - \gamma }}{{2m}} \pm \frac{{\sqrt {{\gamma ^2} - 4mk} }}{{2m}} = \lambda \pm \mu \,i\]where the real part is guaranteed to be negative and so the displacement is
\[\begin{align*}u\left( t \right) & = {c_1}{{\bf{e}}^{\lambda t}}\cos \left( {\mu t} \right) + {c_2}{{\bf{e}}^{\lambda t}}\sin \left( {\mu t} \right)\\ & = {{\bf{e}}^{\lambda t}}\left( {{c_1}\cos \left( {\mu t} \right) + {c_2}\sin \left( {\mu t} \right)} \right)\\ & = R{{\bf{e}}^{\lambda t}}\cos \left( {\mu t - \delta } \right)\end{align*}\]Notice that we reduced the sine and cosine down to a single cosine in this case as we did in the undamped case. Also, since \(\lambda < 0\) the displacement will approach zero as \(t \to \infty \) and the damper will also work as it’s supposed to in this case.
We will get this case will occur when
\[\begin{align*}{\gamma ^2} & < 4mk\\ \gamma & < 2\sqrt {mk} \\ \gamma & < {\gamma _{CR}}\end{align*}\]and is called under damping.
Let’s take a look at a couple of examples here with damping.
The mass and spring constant were already found in the first example so we won’t do the work here. We do need to find the damping coefficient however. To do this we will use the formula for the damping force given above with one modification. The original damping force formula is,
\[{F_d} = - \gamma u'\]However, remember that the force and the velocity are always acting in opposite directions. So, if the velocity is upward (i.e. negative) the force will be downward (i.e. positive) and so the minus in the formula will cancel against the minus in the velocity. Likewise, if the velocity is downward (i.e. positive) the force will be upwards (i.e. negative) and in this case the minus sign in the formula will cancel against the minus in the force. In other words, we can drop the minus sign in the formula and use
\[{F_d} = \gamma u'\]and then just ignore any signs for the force and velocity.
Doing this gives us the following for the damping coefficient
\[12 = \gamma \left( 2 \right)\hspace{0.25in} \Rightarrow \hspace{0.25in}\gamma = 6\]The IVP for this example is then,
\[\frac{1}{2}u'' + 6u' + 18u = 0\hspace{0.25in}u\left( 0 \right) = - \frac{1}{2}\hspace{0.25in}u'\left( 0 \right) = 1\]Before solving let’s check to see what kind of damping we’ve got. To do this all we need is the critical damping coefficient.
\[{\gamma _{CR}} = 2\sqrt {km} = 2\sqrt {\left( {18} \right)\left( {\frac{1}{2}} \right)} = 2\sqrt 9 = 6\]So, it looks like we’ve got critical damping. Note that this means that when we go to solve the differential equation we should get a double root.
Speaking of solving, let’s do that. I’ll leave the details to you to check that the displacement at any time \(t\) is.
\[u\left( t \right) = - \frac{1}{2}{{\bf{e}}^{ - 6t}} - 2t{{\bf{e}}^{ - 6t}}\]Here is a sketch of the displacement during the first 3 seconds.
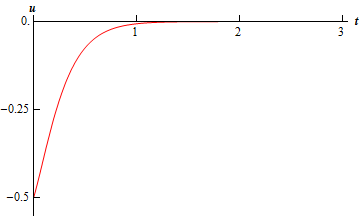
Notice that the “vibration” in the system is not really a true vibration as we tend to think of them. In the critical damping case there isn’t going to be a real oscillation about the equilibrium point that we tend to associate with vibrations. The damping in this system is strong enough to force the “vibration” to die out before it ever really gets a chance to do much in the way of oscillation.
So, the only difference between this example and the previous example is damping force. So, let’s find the damping coefficient
\[17 = \gamma \left( 2 \right)\hspace{0.25in} \Rightarrow \hspace{0.25in}\gamma = \frac{{17}}{2} = 8.5 > {\gamma _{CR}}\]So, it looks like we’ve got over damping this time around so we should expect to get two real distinct roots from the characteristic equation and they should both be negative. The IVP for this example is,
\[\frac{1}{2}u'' + \frac{{17}}{2}u' + 18u = 0\hspace{0.25in}u\left( 0 \right) = - \frac{1}{2}\hspace{0.25in}u'\left( 0 \right) = 1\]This one’s a little messier than the previous example so we’ll do a couple of the steps, leaving it to you to fill in the blanks. The roots of the characteristic equation are
\[{r_{1,2}} = \frac{{ - 17 \pm \sqrt {145} }}{2} = - 2.4792,\,\, - 14.5208\]In this case it will be easier to just convert to decimals and go that route. Note that, as predicted we got two real, distinct and negative roots. The general and actual solution for this example are then,
\[\begin{align*}u\left( t \right) & = {c_1}{{\bf{e}}^{ - 2.4792\,\,t}} + {c_2}{{\bf{e}}^{ - 14.5208\,\,t}}\\ u\left( t \right) & = - 0.5198{{\bf{e}}^{ - 2.4792\,\,t}} + 0.0199{{\bf{e}}^{ - 14.5208\,\,t}}\end{align*}\]Here’s a sketch of the displacement for this example.
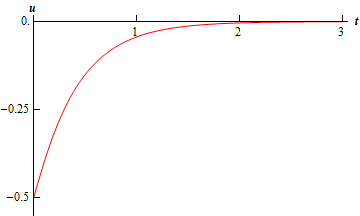
Notice an interesting thing here about the displacement here. Even though we are “over” damped in this case, it actually takes longer for the vibration to die out than in the critical damping case. Sometimes this happens, although it will not always be the case that over damping will allow the vibration to continue longer than the critical damping case.
Also notice that, as with the critical damping case, we don’t get a vibration in the sense that we usually think of them. Again, the damping is strong enough to force the vibration do die out quick enough so that we don’t see much, if any, of the oscillation that we typically associate with vibrations.
Let’s take a look at one more example before moving on the next type of vibrations.
So, let’s get the damping coefficient.
\[5 = \gamma \left( 2 \right)\hspace{0.25in} \Rightarrow \hspace{0.25in}\gamma = \frac{5}{2} = 2.5 < {\gamma _{CR}}\]So, it’s under damping this time. That shouldn’t be too surprising given the first two examples. The IVP for this example is,
\[\frac{1}{2}u'' + \frac{5}{2}u' + 18u = 0\hspace{0.25in}u\left( 0 \right) = - \frac{1}{2}\hspace{0.25in}u'\left( 0 \right) = 1\]In this case the roots of the characteristic equation are
\[{r_{1,2}} = \frac{{ - 5 \pm \sqrt {119} \,i}}{2}\]They are complex as we expected to get since we are in the under damped case. The general solution and actual solution are
\[\begin{align*}u\left( t \right) & = {{\bf{e}}^{ - \frac{{5t}}{2}}}\left( {{c_1}\cos \left( {\frac{{\sqrt {119} }}{2}t} \right) + {c_2}\sin \left( {\frac{{\sqrt {119} }}{2}t} \right)} \right)\\ u\left( t \right) & = {{\bf{e}}^{ - \frac{{5t}}{2}}}\left( { - 0.5\cos \left( {\frac{{\sqrt {119} }}{2}t} \right) - 0.04583\sin \left( {\frac{{\sqrt {119} }}{2}t} \right)} \right)\end{align*}\]Let’s convert this to a single cosine as we did in the undamped case.
\[\begin{align*}R & = \sqrt {{{\left( { - 0.5} \right)}^2} + {{\left( { - 0.04583} \right)}^2}} = 0.502096\\ {\delta _1} & = {\tan ^{ - 1}}\left( {\frac{{ - 0.04583}}{{ - 0.5}}} \right) = 0.09051\hspace{0.25in}{\mbox{OR}}\hspace{0.25in}{\delta _2} = {\delta _1} + \pi = 3.2321\end{align*}\]As with the undamped case we can use the coefficients of the cosine and the sine to determine which phase shift that we should use. The coefficient of the cosine (\(c_{1}\)) is negative and so \(\cos \delta \) must also be negative. Likewise, the coefficient of the sine (\(c_{2}\)) is also negative and so \(\sin \delta \) must also be negative. This means that \(\delta \) must be in the Quadrant III and so the second angle is the one that we want.
The displacement is then
\[u\left( t \right) = 0.502096{{\bf{e}}^{ - \frac{{5t}}{2}}}\cos \left( {\frac{{\sqrt {119} }}{2}t - 3.2321} \right)\]Here is a sketch of this displacement.
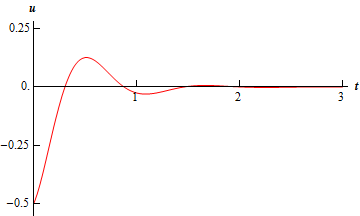
In this case we finally got what we usually consider to be a true vibration. In fact, that is the point of critical damping. As we increase the damping coefficient, the critical damping coefficient will be the first one in which a true oscillation in the displacement will not occur. For all values of the damping coefficient larger than this (i.e. over damping) we will also not see a true oscillation in the displacement.
From a physical standpoint critical (and over) damping is usually preferred to under damping. Think of the shock absorbers in your car. When you hit a bump you don’t want to spend the next few minutes bouncing up and down while the vibration set up by the bump die out. You would like there to be as little movement as possible. In other words, you will want to set up the shock absorbers in your car so get at the least critical damping so that you can avoid the oscillations that will arise from an under damped case.
It’s now time to look at systems in which we allow other external forces to act on the object in the system.
Undamped, Forced Vibrations
We will first take a look at the undamped case. The differential equation in this case is
\[mu'' + ku = F\left( t \right)\]This is just a nonhomogeneous differential equation and we know how to solve these. The general solution will be
\[u\left( t \right) = {u_c}\left( t \right) + {U_P}\left( t \right)\]where the complementary solution is the solution to the free, undamped vibration case. To get the particular solution we can use either undetermined coefficients or variation of parameters depending on which we find easier for a given forcing function.
There is a particular type of forcing function that we should take a look at since it leads to some interesting results. Let’s suppose that the forcing function is a simple periodic function of the form
\[F\left( t \right) = {F_0}\cos \left( {\omega \,t} \right)\hspace{0.25in}{\mbox{OR}}\hspace{0.25in}F\left( t \right) = {F_0}\sin \left( {\omega \,t} \right)\]For the purposes of this discussion we’ll use the first one. Using this, the IVP becomes,
\[mu'' + ku = {F_0}\cos \left( {\omega \,t} \right)\]The complementary solution, as pointed out above, is just
\[{u_c}\left( t \right) = {c_1}\cos \left( {{\omega _0}t} \right) + {c_2}\sin \left( {{\omega _0}t} \right)\]where \({\omega _0}\) is the natural frequency.
We will need to be careful in finding a particular solution. The reason for this will be clear if we use undetermined coefficients. With undetermined coefficients our guess for the form of the particular solution would be,
\[{U_P}\left( t \right) = A\cos \left( {\omega \,t} \right) + B\sin \left( {\omega \,t} \right)\]Now, this guess will be problems if \({\omega _0} = \omega \). If this were to happen the guess for the particular solution is exactly the complementary solution and so we’d need to add in a \(t\). Of course, if we don’t have \({\omega _0} = \omega \) then there will be nothing wrong with the guess.
So, we will need to look at this in two cases.
- \({\omega _0} \ne \omega \)
In this case our initial guess is okay since it won’t be the complementary solution. Upon differentiating the guess and plugging it into the differential equation and simplifying we get,
\[\left( { - m{\omega ^2}A + kA} \right)\cos \left( {\omega t} \right) + \left( { - m{\omega ^2}B + kB} \right)\sin \left( {\omega t} \right) = {F_0}\cos \left( {\omega t} \right)\]Setting coefficients equal gives us,
\[\begin{align*} & \cos \left( {\omega \,t} \right)\,: & \left( { - m{\omega ^2} + k} \right)A & = {F_0} & \Rightarrow \hspace{0.25in}A & = \frac{{{F_0}}}{{k - m{\omega ^2}}}\\ & \sin \left( {\omega \,t} \right)\,: & \left( { - m{\omega ^2} + k} \right)B & = 0 & \Rightarrow \hspace{0.25in}B & = 0\end{align*}\]The particular solution is then
\[\begin{align*}{U_P}\left( t \right) & = \frac{{{F_0}}}{{k - m{\omega ^2}}}\cos \left( {\omega t} \right)\\ & = \frac{{{F_0}}}{{m\left( {\frac{k}{m} - {\omega ^2}} \right)}}\cos \left( {\omega t} \right)\\ & = \frac{{{F_0}}}{{m\left( {\omega _0^2 - {\omega ^2}} \right)}}\cos \left( {\omega t} \right)\end{align*}\]Note that we rearranged things a little. Depending on the form that you’d like the displacement to be in we can have either of the following.
\[\begin{align*}u\left( t \right) & = {c_1}\cos \left( {{\omega _0}t} \right) + {c_2}\sin \left( {{\omega _0}t} \right) + \frac{{{F_0}}}{{m\left( {\omega _0^2 - {\omega ^2}} \right)}}\cos \left( {\omega t} \right)\\ u\left( t \right) & = R\cos \left( {{\omega _0}t - \delta } \right) + \frac{{{F_0}}}{{m\left( {\omega _0^2 - {\omega ^2}} \right)}}\cos \left( {\omega t} \right)\end{align*}\]If we used the sine form of the forcing function we could get a similar formula.
- \({\omega _0} = \omega \)
In this case we will need to add in a \(t\) to the guess for the particular solution.
\[{U_P}\left( t \right) = At\cos \left( {{\omega _0}t} \right) + Bt\sin \left( {{\omega _0}t} \right)\]Note that we went ahead and acknowledge that \({\omega _0} = \omega \) in our guess. Acknowledging this will help with some simplification that we’ll need to do later on. Differentiating our guess, plugging it into the differential equation and simplifying gives us the following.
\[\begin{align*}& \left( { - m\omega _0^2 + k} \right)At\cos \left( {\omega t} \right) + \left( { - m\omega _0^2 + k} \right)Bt\sin \left( {\omega t} \right) + \\ & \hspace{1.5in}2m{\omega _0}B\cos \left( {\omega t} \right) - 2m{\omega _0}A\sin \left( {\omega t} \right) = {F_0}\cos \left( {\omega t} \right)\end{align*}\]Before setting coefficients equal, let’s remember the definition of the natural frequency and note that
\[ - m\omega _0^2 + k = - m{\left( {\sqrt {\frac{k}{m}} } \right)^2} + k = - m\left( {\frac{k}{m}} \right) + k = 0\]So, the first two terms actually drop out (which is a very good thing…) and this gives us,
\[2m{\omega _0}B\cos \left( {\omega t} \right) - 2m{\omega _0}A\sin \left( {\omega t} \right) = {F_0}\cos \left( {\omega t} \right)\]Now let’s set coefficient equal.
\[\begin{align*} & \cos \left( {\omega t} \right)\,: & 2m{\omega _0}B & = {F_0} & \Rightarrow \hspace{0.25in}B & = \frac{{{F_0}}}{{2m{\omega _0}}}\\ & \sin \left( {\omega t} \right)\,: & 2m{\omega _0}A & = 0 & \Rightarrow \hspace{0.25in}A & = 0\end{align*}\]In this case the particular will be,
\[{U_P}\left( t \right) = \frac{{{F_0}}}{{2m{\omega _0}}}t\sin \left( {{\omega _0}t} \right)\]The displacement for this case is then
\[\begin{align*}u\left( t \right) & = {c_1}\cos \left( {{\omega _0}t} \right) + {c_2}\sin \left( {{\omega _0}t} \right) + \frac{{{F_0}}}{{2m{\omega _0}}}t\sin \left( {{\omega _0}t} \right)\\ u\left( t \right) & = R\cos \left( {{\omega _0}t - \delta } \right) + \frac{{{F_0}}}{{2m{\omega _0}}}t\sin \left( {{\omega _0}t} \right)\end{align*}\]depending on the form that you prefer for the displacement.
So, what was the point of the two cases here? Well in the first case, \({\omega _0} \ne \omega \) our displacement function consists of two cosines and is nice and well behaved for all time.
In contrast, the second case, \({\omega _0} = \omega \) will have some serious issues at \(t\) increases. The addition of the \(t\) in the particular solution will mean that we are going to see an oscillation that grows in amplitude as \(t\) increases. This case is called resonance and we would generally like to avoid this at all costs.
In this case resonance arose by assuming that the forcing function was,
\[F\left( t \right) = {F_0}\cos \left( {{\omega _0}\,t} \right)\]We would also have the possibility of resonance if we assumed a forcing function of the form.
\[F\left( t \right) = {F_0}\sin \left( {{\omega _0}\,t} \right)\]We should also take care to not assume that a forcing function will be in one of these two forms. Forcing functions can come in a wide variety of forms. If we do run into a forcing function different from the one that used here you will have to go through undetermined coefficients or variation of parameters to determine the particular solution.
is attached to the object and the system will experience resonance. If the object is initially displaced 20 cm downward from its equilibrium position and given a velocity of 10 cm/sec upward find the displacement at any time \(t\).
Since we are in the metric system we won’t need to find mass as it’s been given to us. Also, for all calculations we’ll be converting all lengths over to meters.
The first thing we need to do is find \(k\).
\[k = \frac{{mg}}{L} = \frac{{\left( 3 \right)\left( {9.8} \right)}}{{0.392}} = 75\]Now, we are told that the system experiences resonance so let’s go ahead and get the natural frequency so we can completely set up the IVP.
\[{\omega _0} = \sqrt {\frac{k}{m}} = \sqrt {\frac{{75}}{3}} = 5\]The IVP for this is then
\[3u'' + 75u = 10\cos \left( {5t} \right)\hspace{0.25in}u\left( 0 \right) = 0.2\hspace{0.25in}u'\left( 0 \right) = - 0.1\]Solution wise there isn’t a whole lot to do here. The complementary solution is the free undamped solution which is easy to get and for the particular solution we can just use the formula that we derived above.
The general solution is then,
\[\begin{align*}u\left( t \right) & = {c_1}\cos \left( {5t} \right) + {c_2}\sin \left( {5t} \right) + \frac{{10}}{{2\left( 3 \right)\left( 5 \right)}}t\sin \left( {5t} \right)\\ u\left( t \right) & = {c_1}\cos \left( {5t} \right) + {c_2}\sin \left( {5t} \right) + \frac{1}{3}t\sin \left( {5t} \right)\end{align*}\]Applying the initial conditions gives the displacement at any time \(t\). We’ll leave the details to you to check.
\[u\left( t \right) = \frac{1}{5}\cos \left( {5t} \right) - \frac{1}{{50}}\sin \left( {5t} \right) + \frac{1}{3}t\sin \left( {5t} \right)\]The last thing that we’ll do is combine the first two terms into a single cosine.
\[\begin{align*}R & = \sqrt {{{\left( {\frac{1}{5}} \right)}^2} + {{\left( { - \frac{1}{{50}}} \right)}^2}} = 0.200998\\ {\delta _1} & = {\tan ^{ - 1}}\left( {\frac{{ - {}^{1}/{}_{{50}}}}{{{}^{1}/{}_{5}}}} \right) = - 0.099669\hspace{0.25in}{\delta _2} = {\delta _1} + \pi = 3.041924\end{align*}\]In this case the coefficient of the cosine is positive and the coefficient of the sine is negative. This forces \(\cos \delta \) to be positive and \(\sin \delta \) to be negative. This means that the phase shift needs to be in Quadrant IV and so the first one is the correct phase shift this time.
The displacement then becomes,
\[u\left( t \right) = 0.200998\cos \left( {5t + 0.099669} \right) + \frac{1}{3}t\sin \left( {5t} \right)\]Here is a sketch of the displacement for this example.
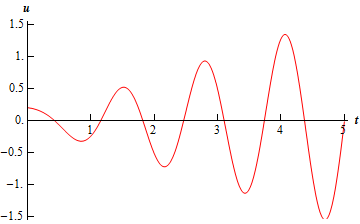
It’s now time to look at the final vibration case.
Forced, Damped Vibrations
This is the full blown case where we consider every last possible force that can act upon the system. The differential equation for this case is,
\[mu'' + \gamma u' + ku = F\left( t \right)\]The displacement function this time will be,
\[u\left( t \right) = {u_c}\left( t \right) + {U_P}\left( t \right)\]where the complementary solution will be the solution to the free, damped case and the particular solution will be found using undetermined coefficients or variation of parameter, whichever is most convenient to use.
There are a couple of things to note here about this case. First, from our work back in the free, damped case we know that the complementary solution will approach zero as \(t\) increases. Because of this the complementary solution is often called the transient solution in this case.
Also, because of this behavior the displacement will start to look more and more like the particular solution as \(t\) increases and so the particular solution is often called the steady state solution or forced response.
Let’s work one final example before leaving this section. As with the previous examples, we’re going to leave most of the details out for you to check.
So, all we need to do is compute the damping coefficient for this problem then pull everything else down from the previous problem. The damping coefficient is
\[\begin{align*}{F_d} & = \gamma u'\\ 45 & = \gamma \left( {0.5} \right)\\ \gamma & = 90\end{align*}\]The IVP for this problem is.
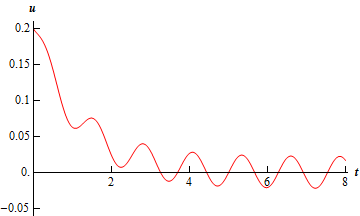
\[3u'' + 90u' + 75u = 10\cos \left( {5t} \right)\hspace{0.25in}u\left( 0 \right) = 0.2\hspace{0.25in}u'\left( 0 \right) = - 0.1\]The complementary solution for this example is
\[\begin{align*}{u_c}\left( t \right) & = {c_1}{{\bf{e}}^{\left( { - 15 + 10\sqrt 2 } \right)t}} + {c_2}{{\bf{e}}^{\left( { - 15 - 10\sqrt 2 } \right)t}}\\ {u_c}\left( t \right) & = {c_1}{{\bf{e}}^{ - 0.8579t}} + {c_2}{{\bf{e}}^{ - 29.1421t}}\end{align*}\]For the particular solution we the form will be,
\[{U_P}\left( t \right) = A\cos \left( {5t} \right) + B\sin \left( {5t} \right)\]Plugging this into the differential equation and simplifying gives us,
\[450B\cos \left( {5t} \right) - 450A\sin \left( {5t} \right) = 10\cos \left( {5t} \right)\]Setting coefficient equal gives,
\[{U_P}\left( t \right) = \frac{1}{{45}}\sin \left( {5t} \right)\]The general solution is then
\[u\left( t \right) = {c_1}{{\bf{e}}^{ - 0.8579t}} + {c_2}{{\bf{e}}^{ - 29.1421t}} + \frac{1}{{45}}\sin \left( {5t} \right)\]Applying the initial condition gives
\[u\left( t \right) = 0.1986{{\bf{e}}^{ - 0.8579t}} + 0.001398{{\bf{e}}^{ - 29.1421t}} + \frac{1}{{45}}\sin \left( {5t} \right)\]Here is a sketch of the displacement for this example.