Example 1  Determine the volume of the solid obtained by rotating the region bounded by  and the x-axis about the y-axis.

Solution

As we did in the previous section, let’s first graph the bounded region and solid.  Note that the bounded region here is the shaded portion shown.  The curve is extended out a little past this for the purposes of illustrating what the curve looks like.

So, we’ve basically got something that’s roughly doughnut shaped.  If we were to use rings on this solid here is what a typical ring would look like.

This leads to several problems.  First, both the inner and outer radius are defined by the same function.  This, in itself, can be dealt with on occasion as we saw in a example in the Area Between Curves section.  However, this usually means more work than other methods so it’s often not the best approach.

This leads to the second problem we got here.  In order to use rings we would need to put this function into the form .  That is NOT easy in general for a cubic polynomial and in other cases may not even be possible to do.   Even when it is possible to do this the resulting equation is often significantly messier than the original which can also cause problems.

The last problem with rings in this case is not so much a problem as its just added work.  If we were to use rings the limit would be y limits and this means that we will need to know how high the graph goes.  To this point the limits of integration have always been intersection points that were fairly easy to find.  However, in this case the highest point is not an intersection point, but instead a relative maximum.   We spent several sections in the Applications of Derivatives chapter talking about how to find maximum values of functions.  However, finding them can, on occasion, take some work.

So, we’ve seen three problems with rings in this case that will either increase our work load or outright prevent us from using rings.

What we need to do is to find a different way to cut the solid that will give us a cross-sectional area that we can work with.  One way to do this is to think of our solid as a lump of cookie dough and instead of cutting it perpendicular to the axis of rotation we could instead center a cylindrical cookie cutter on the axis of rotation and push this down into the solid.  Doing this would give the following picture,

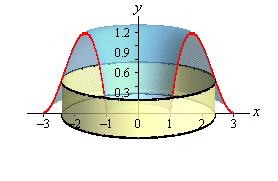
Doing this gives us a cylinder or shell in the object and we can easily find its surface area.  The surface area of this cylinder is,

Notice as well that as we increase the radius of the cylinder we will completely cover the solid and so we can use this in our formula to find the volume of this solid.  All we need are limits of integration.  The first cylinder will cut into the solid at  and as we increase x to  we will completely cover both sides of the solid since expanding the cylinder in one direction will automatically expand it in the other direction as well.

The volume of this solid is then,

Example 2  Determine the volume of the solid obtained by rotating the region bounded by ,  and the x-axis about the x-axis.

Solution

First let’s get a graph of the bounded region and the solid.

Okay, we are rotating about a horizontal axis.  This means that the area will be a function of y and so our equation will also need to be wrote in  form.

As we did in the ring/disk section let’s take a couple of looks at a typical cylinder.  The sketch on the left shows a typical cylinder with the back half of the object also in the sketch to give the right sketch some context.  The sketch on the right contains a typical cylinder and only the curves that define the edge of the solid.

In this case the width of the cylinder is not the function value as it was in the previous example.  In this case the function value is the distance between the edge of the cylinder and the y-axis.  The distance from the edge out to the line is  and so the width is then .   The cross sectional area in this case is,

The first cylinder will cut into the solid at  and the final cylinder will cut in at  and so these are our limits of integration.

The volume of this solid is,

Example 3  Determine the volume of the solid obtained by rotating the region bounded by  and  about the line .

Solution

Here’s a graph of the bounded region and solid.

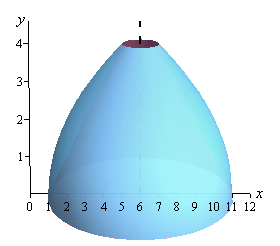
Here are our sketches of a typical cylinder.  Again, the sketch on the left is here to provide some context for the sketch on the right.

Okay, there is a lot going on in the sketch to the left.  First notice that the radius is not just an x or y as it was in the previous two cases.  In this case x is the distance from the x-axis to the edge of the cylinder and we need the distance from the axis of rotation to the edge of the cylinder.  That means that the radius of this cylinder is .

Secondly, the height of the cylinder is the difference of the two functions in this case.

The cross sectional area is then,

Now the first cylinder will cut into the solid at  and the final cylinder will cut into the solid at   so there are our limits.

Here is the volume.

The integration of the last term is a little tricky so let’s do that here.  It will use the substitution,

We saw one of these kinds of substitutions back in the substitution section.

Example 4  Determine the volume of the solid obtained by rotating the region bounded by  and  about the line .

Solution

We should first get the intersection points there.

So, the two curves will intersect at  and .  Here is a sketch of the bounded region and the solid.

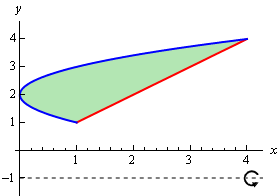
Here are our sketches of a typical cylinder.  Tthe sketch on the left is here to provide some context for the sketch on the right.

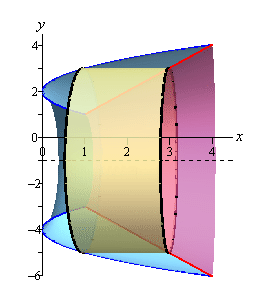
Here’s the cross sectional area for this cylinder.

The first cylinder will cut into the solid at  and the final cylinder will cut in at .  The volume is then,