This is a fairly simple proof. We’ll assume that \(f\left( x \right)\) has a relative maximum to do the proof. The proof for a relative minimum is nearly identical. So, if we assume that we have a relative maximum at \(x = c\) then we know that \(f\left( c \right) \ge f\left( x \right)\) for all \(x\) that are sufficiently close to \(x = c\). In particular for all \(h\) that are sufficiently close to zero (positive or negative) we must have,

\[f\left( c \right) \ge f\left( {c + h} \right)\]

or, with a little rewrite we must have,

\[\begin{equation}f\left( {c + h} \right) - f\left( c \right) \le 0 \label{eq:eq1}\end{equation}\]

Now, at this point assume that \(h > 0\) and divide both sides of \(\eqref{eq:eq1}\) by \(h\). This gives,

\[\frac{{f\left( {c + h} \right) - f\left( c \right)}}{h} \le 0\]

Because we’re assuming that \(h > 0\) we can now take the right-hand limit of both sides of this.

\[\mathop {\lim }\limits_{h \to {0^ + }} \frac{{f\left( {c + h} \right) - f\left( c \right)}}{h} \le \mathop {\lim }\limits_{h \to {0^ + }} 0 = 0\]

We are also assuming that \(f'\left( c \right)\) exists and recall that if a normal limit exists then it must be equal to both one-sided limits. We can then say that,

\[f'\left( c \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {c + h} \right) - f\left( c \right)}}{h} = \mathop {\lim }\limits_{h \to {0^ + }} \frac{{f\left( {c + h} \right) - f\left( c \right)}}{h} \le 0\]

If we put this together we have now shown that \(f'\left( c \right) \le 0\).

Okay, now let’s turn things around and assume that \(h < 0\) and divide both sides of \(\eqref{eq:eq1}\) by \(h\). This gives,

\[\frac{{f\left( {c + h} \right) - f\left( c \right)}}{h} \ge 0\]

Remember that because we’re assuming \(h < 0\) we’ll need to switch the inequality when we divide by a negative number. We can now do a similar argument as above to get that,

\[f'\left( c \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {c + h} \right) - f\left( c \right)}}{h} = \mathop {\lim }\limits_{h \to {0^ - }} \frac{{f\left( {c + h} \right) - f\left( c \right)}}{h} \ge \mathop {\lim }\limits_{h \to {0^ - }} 0 = 0\]

The difference here is that this time we’re going to be looking at the left-hand limit since we’re assuming that \(h < 0\). This argument shows that \(f'\left( c \right) \ge 0\).

We’ve now shown that \(f'\left( c \right) \le 0\) and \(f'\left( c \right) \ge 0\). Then only way both of these can be true at the same time is to have \(f'\left( c \right) = 0\) and this in turn means that \(x = c\) must be a critical point.

As noted above, if we assume that \(f\left( x \right)\) has a relative minimum then the proof is nearly identical and so isn’t shown here. The main differences are simply some inequalities need to be switched.

Let \({x_1}\) and \({x_2}\) be in \(I\) and suppose that \({x_1} < {x_2}\). Now, using the Mean Value Theorem on \(\left[ {{x_1},{x_2}} \right]\) means there is a number \(c\) such that \({x_1} < c < {x_2}\) and,

\[f\left( {{x_2}} \right) - f\left( {{x_1}} \right) = f'\left( c \right)\left( {{x_2} - {x_1}} \right)\]

Because \({x_1} < c < {x_2}\) we know that \(c\) must also be in \(I\) and so we know that \(f'\left( c \right) > 0\) we also know that \({x_2} - {x_1} > 0\). So, this means that we have,

\[f\left( {{x_2}} \right) - f\left( {{x_1}} \right) > 0\]

Rewriting this gives,

\[f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\]

and so, by definition, since \({x_1}\) and \({x_2}\) were two arbitrary numbers in \(I\), \(f\left( x \right)\)must be increasing on \(I\).

This proof is nearly identical to the previous part.

Let \({x_1}\) and \({x_2}\) be in \(I\) and suppose that \({x_1} < {x_2}\). Now, using the Mean Value Theorem on \(\left[ {{x_1},{x_2}} \right]\) means there is a number \(c\) such that \({x_1} < c < {x_2}\) and,

\[f\left( {{x_2}} \right) - f\left( {{x_1}} \right) = f'\left( c \right)\left( {{x_2} - {x_1}} \right)\]

Because \({x_1} < c < {x_2}\) we know that \(c\) must also be in \(I\) and so we know that \(f'\left( c \right) < 0\) we also know that \({x_2} - {x_1} > 0\). So, this means that we have,

\[f\left( {{x_2}} \right) - f\left( {{x_1}} \right) < 0\]

Rewriting this gives,

\[f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\]

and so, by definition, since \({x_1}\) and \({x_2}\) were two arbitrary numbers in \(I\), \(f\left( x \right)\)must be decreasing on \(I\).

Again, this proof is nearly identical to the previous two parts, but in this case is actually somewhat easier.

Let \({x_1}\) and \({x_2}\) be in \(I\). Now, using the Mean Value Theorem on \(\left[ {{x_1},{x_2}} \right]\) there is a number \(c\) such that \(c\) is between \({x_1}\) and \({x_2}\) and,

\[f\left( {{x_2}} \right) - f\left( {{x_1}} \right) = f'\left( c \right)\left( {{x_2} - {x_1}} \right)\]

Note that for this part we didn’t need to assume that \({x_1} < {x_2}\) and so all we know is that \(c\) is between \({x_1}\) and \({x_2}\) and so, more importantly, \(c\) is also in \(I\). and this means that \(f'\left( c \right) = 0\). So, this means that we have,

\[f\left( {{x_2}} \right) - f\left( {{x_1}} \right) = 0\]

Rewriting this gives,

\[f\left( {{x_1}} \right) = f\left( {{x_2}} \right)\]

and so, since \({x_1}\) and \({x_2}\) were two arbitrary numbers in \(I\), \(f\left( x \right)\)must be constant on \(I\).

Let \(a\) be any number in the interval \(I\). The tangent line to \(f\left( x \right)\) at \(x = a\) is,

\[y = f\left( a \right) + f'\left( a \right)\left( {x - a} \right)\]

To show that \(f\left( x \right)\) is concave up on \(I\) then we need to show that for any \(x\), \(x \ne a\), in \(I\) that,

\[f\left( x \right) > f\left( a \right) + f'\left( a \right)\left( {x - a} \right)\]

or in other words, the tangent line is always below the graph of \(f\left( x \right)\) on \(I\). Note that we require \(x \ne a\) because at that point we know that \(f\left( x \right) = f\left( a \right)\) since we are talking about the tangent line.

Let’s start the proof off by first assuming that \(x > a\). Using the Mean Value Theorem on \(\left[ {a,x} \right]\) means there is a number \(c\) such that \(a < c < x\) and,

\[f\left( x \right) - f\left( a \right) = f'\left( c \right)\left( {x - a} \right)\]

With some rewriting this is,

\[\begin{equation}f\left( x \right) = f\left( a \right) + f'\left( c \right)\left( {x - a} \right) \label{eq:eq2}\end{equation}\]

Next, let’s use the fact that \(f''\left( x \right) > 0\) for every \(x\) on \(I\). This means that the first derivative, \(f'\left( x \right)\), must be increasing (because its derivative, \(f''\left( x \right)\), is positive). Now, we know from the Mean Value Theorem that \(a < c\) and so because \(f'\left( x \right)\) is increasing we must have,

\[\begin{equation}f'\left( a \right) < f'\left( c \right) \label{eq:eq3} \end{equation}\]

Recall as well that we are assuming \(x > a\) and so \(x - a > 0\). If we now multiply \(\eqref{eq:eq3}\) by \(x - a\) (which is positive and so the inequality stays the same) we get,

\[f'\left( a \right)\left( {x - a} \right) < f'\left( c \right)\left( {x - a} \right)\]

Next, add \(f\left( a \right)\) to both sides of this to get,

\[f\left( a \right) + f'\left( a \right)\left( {x - a} \right) < f\left( a \right) + f'\left( c \right)\left( {x - a} \right)\]

However, by \(\eqref{eq:eq2}\), the right side of this is nothing more than \(f\left( x \right)\) and so we have,

\[f\left( a \right) + f'\left( a \right)\left( {x - a} \right) < f\left( x \right)\]

but this is exactly what we wanted to show.

So, provided \(x > a\) the tangent line is in fact below the graph of \(f\left( x \right)\).

We now need to assume \(x < a\). Using the Mean Value Theorem on \(\left[ {x,a} \right]\) means there is a number \(c\) such that \(x < c < a\) and,

\[f\left( a \right) - f\left( x \right) = f'\left( c \right)\left( {a - x} \right)\]

If we multiply both sides of this by –1 and then adding \(f\left( a \right)\) to both sides and we again arise at \(\eqref{eq:eq2}\).

Now, from the Mean Value Theorem we know that \(c < a\) and because \(f''\left( x \right) > 0\) for every \(x\) on \(I\) we know that the derivative is still increasing and so we have,

\[f'\left( c \right) < f'\left( a \right)\]

Let’s now multiply this by \(x - a\), which is now a negative number since \(x < a\). This gives,

\[f'\left( c \right)\left( {x - a} \right) > f'\left( a \right)\left( {x - a} \right)\]

Notice that we had to switch the direction of the inequality since we were multiplying by a negative number. If we now add \(f\left( a \right)\) to both sides of this and then substitute \(\eqref{eq:eq2}\) into the results we arrive at,

\[\begin{align*}f\left( a \right) + f'\left( c \right)\left( {x - a} \right) & > f\left( a \right) + f'\left( a \right)\left( {x - a} \right)\\ & f\left( x \right) > f\left( a \right) + f'\left( a \right)\left( {x - a} \right)\end{align*}\]

So, again we’ve shown that the tangent line is always below the graph of \(f\left( x \right)\).

We’ve now shown that if \(x\) is any number in \(I\), with \(x \ne a\) the tangent lines are always below the graph of \(f\left( x \right)\) on \(I\) and so \(f\left( x \right)\) is concave up on \(I\).

This proof is nearly identical to the proof of 1 and since that proof is fairly long we’re going to just get things started and then leave the rest of it to you to go through.

Let \(a\) be any number in \(I\) . To show that \(f\left( x \right)\) is concave down we need to show that for any \(x\) in \(I\), \(x \ne a\), that the tangent line is always above the graph of \(f\left( x \right)\) or,

\[f\left( x \right) < f\left( a \right) + f'\left( a \right)\left( {x - a} \right)\]

From this point on the proof is almost identical to the proof of 1 except that you’ll need to use the fact that the derivative in this case is decreasing since \(f''\left( x \right) < 0\). We’ll leave it to you to fill in the details of this proof.

First since we are assuming that \(f''\left( x \right)\) is continuous in a region around \(x = c\) then we can assume that in fact \(f''\left( c \right) < 0\) is also true in some open region, say \(\left( {a,b} \right)\) around \(x = c\), i.e. \(a < c < b\).

Now let \(x\) be any number such that \(a < x < c\), we’re going to use the Mean Value Theorem on \(\left[ {x,c} \right]\). However, instead of using it on the function itself we’re going to use it on the first derivative. So, the Mean Value Theorem tells us that there is a number \(x < d < c\) such that,

\[f'\left( c \right) - f'\left( x \right) = f''\left( d \right)\left( {c - x} \right)\]

Now, because \(a < x < d < c\) we know that \(f''\left( d \right) < 0\) and we also know that \(c - x > 0\) so we then get that,

\[f'\left( c \right) - f'\left( x \right) < 0\]

However, we also assumed that \(f'\left( c \right) = 0\) and so we have,

\[ - f'\left( x \right) < 0\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}f'\left( x \right) > 0\]

Or, in other words to the left of \(x = c\) the function is increasing.

Let’s now turn things around and let \(x\) be any number such that \(c < x < b\) and use the Mean Value Theorem on \(\left[ {c,x} \right]\) and the first derivative. The Mean Value Theorem tells us that there is a number \(c < d < x\) such that,

\[f'\left( x \right) - f'\left( c \right) = f''\left( d \right)\left( {x - c} \right)\]

Now, because \(c < d < x < b\) we know that \(f''\left( d \right) < 0\) and we also know that \(x - c > 0\) so we then get that,

\[f'\left( x \right) - f'\left( c \right) < 0\]

Again, use the fact that we also assumed that \(f'\left( c \right) = 0\) to get,

\[f'\left( x \right) < 0\]

We now know that to the right of \(x = c\) the function is decreasing.

So, to the left of \(x = c\) the function is increasing and to the right of \(x = c\) the function is decreasing so by the first derivative test this means that \(x = c\) must be a relative maximum.

This proof is nearly identical to the proof of 1 and since that proof is somewhat long we’re going to leave the proof to you to do. In this case the only difference is that now we are going to assume that \(f''\left( x \right) < 0\) and that will give us the opposite signs of the first derivative on either side of \(x = c\) which gives us the conclusion we were after. We’ll leave it to you to fill in all the details of this.

There isn’t really anything to prove here. All this statement says is that any of the three cases are possible and to “prove” this all one needs to do is provide an example of each of the three cases. This was done in The Shape of a Graph, Part II section where this test was presented so we’ll leave it to you to go back to that section to see those graphs to verify that all three possibilities really can happen.

We’ll need to do this with 3 cases.

Case 1 : \(f\left( x \right) = k\) on \(\left[ {a,b} \right]\) where \(k\) is a constant.
In this case \(f'\left( x \right) = 0\) for all \(x\) in \(\left[ {a,b} \right]\) and so we can take \(c\) to be any number in \(\left[ {a,b} \right]\).

Case 2 : There is some number \(d\) in \(\left( {a,b} \right)\) such that \(f\left( d \right) > f\left( a \right)\).
Because \(f\left( x \right)\) is continuous on \(\left[ {a,b} \right]\) by the Extreme Value Theorem we know that \(f\left( x \right)\) will have a maximum somewhere in \(\left[ {a,b} \right]\). Also, because \(f\left( a \right) = f\left( b \right)\) and \(f\left( d \right) > f\left( a \right)\) we know that in fact the maximum value will have to occur at some \(c\) that is in the open interval \(\left( {a,b} \right)\), or \(a < c < b\). Because \(c\) occurs in the interior of the interval this means that \(f\left( x \right)\) will actually have a relative maximum at \(x = c\) and by the second hypothesis above we also know that \(f'\left( c \right)\) exists. Finally, by Fermat’s Theorem we then know that in fact \(x = c\) must be a critical point and because we know that \(f'\left( c \right)\) exists we must have \(f'\left( c \right) = 0\) (as opposed to \(f'\left( c \right)\) not existing…).

Case 3 : There is some number \(d\) in \(\left( {a,b} \right)\) such that \(f\left( d \right) < f\left( a \right)\).
This is nearly identical to Case 2 so we won’t put in quite as much detail. By the Extreme Value Theorem \(f\left( x \right)\) will have minimum in \(\left[ {a,b} \right]\) and because \(f\left( a \right) = f\left( b \right)\) and \(f\left( d \right) < f\left( a \right)\) we know that the minimum must occur at \(x = c\) where \(a < c < b\). Finally, by Fermat’s Theorem we know that \(f'\left( c \right) = 0\).

For illustration purposes let’s suppose that the graph of \(f\left( x \right)\) is,

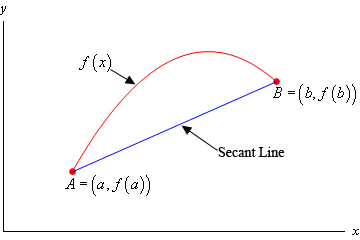
Note of course that it may not look like this, but we just need a quick sketch to make it easier to see what we’re talking about here.

The first thing that we need is the equation of the secant line that goes through the two points \(A\) and \(B\) as shown above. This is,

\[y = f\left( a \right) + \frac{{f\left( b \right) - f\left( a \right)}}{{b - a}}\left( {x - a} \right)\]

Let’s now define a new function, \(g\left( x \right)\), as to be the difference between \(f\left( x \right)\) and the equation of the secant line or,

\[g\left( x \right) = f\left( x \right) - \left( {f\left( a \right) + \frac{{f\left( b \right) - f\left( a \right)}}{{b - a}}\left( {x - a} \right)} \right) = f\left( x \right) - f\left( a \right) - \frac{{f\left( b \right) - f\left( a \right)}}{{b - a}}\left( {x - a} \right)\]

Next, let’s notice that because \(g\left( x \right)\) is the sum of \(f\left( x \right)\), which is assumed to be continuous on \(\left[ {a,b} \right]\), and a linear polynomial, which we know to be continuous everywhere, we know that \(g\left( x \right)\) must also be continuous on \(\left[ {a,b} \right]\).

Also, we can see that \(g\left( x \right)\) must be differentiable on \(\left( {a,b} \right)\) because it is the sum of \(f\left( x \right)\), which is assumed to be differentiable on \(\left( {a,b} \right)\), and a linear polynomial, which we know to be differentiable.

We could also have just computed the derivative as follows,

\[g'\left( x \right) = f'\left( x \right) - \frac{{f\left( b \right) - f\left( a \right)}}{{b - a}}\]

at which point we can see that it exists on \(\left( {a,b} \right)\) because we assumed that \(f'\left( x \right)\) exists on \(\left( {a,b} \right)\) and the last term is just a constant.

Finally, we have,

\[\begin{align*}g\left( a \right) & = f\left( a \right) - f\left( a \right) - \frac{{f\left( b \right) - f\left( a \right)}}{{b - a}}\left( {a - a} \right) = f\left( a \right) - f\left( a \right) = 0\\ & \\ g\left( b \right) & = f\left( b \right) - f\left( a \right) - \frac{{f\left( b \right) - f\left( a \right)}}{{b - a}}\left( {b - a} \right) = f\left( b \right) - f\left( a \right) - \left( {f\left( b \right) - f\left( a \right)} \right) = 0\end{align*}\]

In other words, \(g\left( x \right)\) satisfies the three conditions of Rolle’s Theorem and so we know that there must be a number \(c\) such that \(a < c < b\) and that,

\[0 = g'\left( c \right) = f'\left( c \right) - \frac{{f\left( b \right) - f\left( a \right)}}{{b - a}}\hspace{0.25in} \Rightarrow \hspace{0.25in}f'\left( c \right) = \frac{{f\left( b \right) - f\left( a \right)}}{{b - a}}\]