I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.
Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.
Paul
February 18, 2026
Section 17.6 : Divergence Theorem
In this section we are going to relate surface integrals to triple integrals. We will do this with the Divergence Theorem.
Divergence Theorem
Let \(E\) be a simple solid region and \(S\) is the boundary surface of \(E\) with positive orientation. Let \(\vec F\) be a vector field whose components have continuous first order partial derivatives. Then,
\[\iint\limits_{S}{{\vec F\centerdot d\vec S}} = \iiint\limits_{E}{{{\mathop{\rm div}\nolimits} \vec F\,dV}}\]Let’s see an example of how to use this theorem.
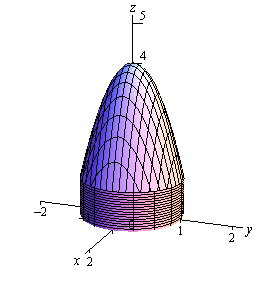
Let’s start this off with a sketch of the surface.
The region \(E\) for the triple integral is then the region enclosed by these surfaces. Note that cylindrical coordinates would be a perfect coordinate system for this region. If we do that here are the limits for the ranges.
\[\begin{array}{c}0 \le z \le 4 - 3{r^2}\\ 0 \le r \le 1\\ 0 \le \theta \le 2\pi \end{array}\]We’ll also need the divergence of the vector field so let’s get that.
\[{\mathop{\rm div}\nolimits} \vec F = y - y + 1 = 1\]The integral is then,
\[\begin{align*}\iint\limits_{S}{{\vec F\centerdot d\vec S}} & = \iiint\limits_{E}{{{\mathop{\rm div}\nolimits} \vec F\,dV}}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\int_{{\,0}}^{{\,1}}{{\int_{{\,0}}^{{4 - 3{r^2}}}{{r\,dz}}\,dr}}\,d\theta }}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\int_{{\,0}}^{{\,1}}{{4r - 3{r^3}\,dr}}\,d\theta }}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\left. {\left( {2{r^2} - \frac{3}{4}{r^4}} \right)} \right|_0^1\,d\theta }}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\frac{5}{4}\,d\theta }}\\ & = \frac{5}{2}\pi \end{align*}\]