Section 2.9 : Continuity

1. The graph of \(f\left( x \right)\) is given below. Based on this graph determine where the function is discontinuous.
   
2. The graph of \(f\left( x \right)\) is given below. Based on this graph determine where the function is discontinuous.
   
3. The graph of \(f\left( x \right)\) is given below. Based on this graph determine where the function is discontinuous.
   

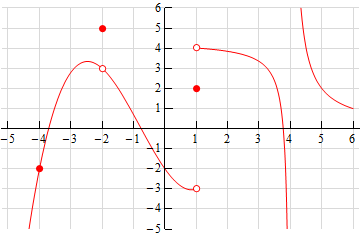
For problems 4 – 13 using only Properties 1- 9 from the Limit Properties section, one-sided limit properties (if needed) and the definition of continuity determine if the given function is continuous or discontinuous at the indicated points.

1. \(\displaystyle f\left( x \right) = \frac{{6 + 2x}}{{7x - 14}}\)
   1. \(x = - 3\)
   2. \(x = 0\)
   3. \(x = 2\)
2. \(\displaystyle R\left( y \right) = \frac{{2y}}{{{y^2} - 25}}\)
   1. \(y = - 5\)
   2. \(y = - 1\)
   3. \(y = 3\)
3. \(\displaystyle g\left( z \right) = \frac{{5z - 20}}{{{z^2} - 12z}}\)
   1. \(z = - 1\)
   2. \(z = 0\)
   3. \(z = 4\)
4. \(\displaystyle W\left( x \right) = \frac{{2 + x}}{{{x^2} + 6x - 7}}\)
   1. \(x = - 7\)
   2. \(x = 0\)
   3. \(x = 1\)
5. \(h\left( z \right) = \left\{ {\begin{array}{rl}{2{z^2}}&{z < - 1}\\{4z + 6}&{z \ge - 1}\end{array}} \right.\)
   1. \(z = - 6\)
   2. \(z = - 1\)
6. \(g\left( x \right) = \left\{ {\begin{array}{rl}{x + {{\bf{e}}^x}}&{x < 0}\\{{x^2}}&{x \ge 0}\end{array}} \right.\)
   1. \(x = 0\)
   2. \(x = 4\)
7. \(Z\left( t \right) = \left\{ {\begin{array}{rl}8&{t < 5}\\{1 - 6t}&{t \ge 5}\end{array}} \right.\)
   1. \(t = 0\)
   2. \(t = 5\)
8. \(h\left( z \right) = \left\{ {\begin{array}{rl}{z + 2}&{z < - 4}\\0&{z = - 4}\\{18 - {z^2}}&{z > - 4}\end{array}} \right.\)
   1. \(z = - 4\)
   2. \(z = 2\)
9. \(f\left( x \right) = \left\{ {\begin{array}{rc}{1 - {x^2}}&{x < 2}\\{ - 3}&{x = 2}\\{2x - 7}&{2 < x < 7}\\0&{x = 7}\\{{x^2}}&{x > 7}\end{array}} \right.\)
   1. \(x = 2\)
   2. \(x = 7\)
10. \(g\left( w \right) = \left\{ {\begin{array}{rc}{3w}&{w < 0}\\0&{w = 0}\\{w + 6}&{0 < w < 8}\\{14}&{w = 8}\\{22 - w}&{w > 8}\end{array}} \right.\)
    1. \(w = 0\)
    2. \(w = 8\)

For problems 14 – 22 determine where the given function is discontinuous.

1. \(\displaystyle f\left( x \right) = \frac{{11 - 2x}}{{2{x^2} - 13x - 7}}\)
2. \(\displaystyle Q\left( z \right) = \frac{3}{{2{z^2} + 3z - 4}}\)
3. \(\displaystyle h\left( t \right) = \frac{{{t^2} - 1}}{{{t^3} + 6{t^2} + t}}\)
4. \(\displaystyle f\left( z \right) = \frac{{4z + 1}}{{5\cos \left( {{\textstyle{z \over 2}}} \right) + 1}}\)
5. \(\displaystyle h\left( x \right) = \frac{{1 - x}}{{x\sin \left( {x - 1} \right)}}\)
6. \(\displaystyle f\left( x \right) = \frac{3}{{4{{\bf{e}}^{x - 7}} - 1}}\)
7. \(\displaystyle R\left( w \right) = \frac{{{{\bf{e}}^{{w^2} + 1}}}}{{{{\bf{e}}^w} - 2{{\bf{e}}^{1 - w}}}}\)
8. \(g\left( x \right) = \cot \left( {4x} \right)\)
9. \(f\left( t \right) = \sec \left( {\sqrt t } \right)\)

For problems 23 – 27 use the Intermediate Value Theorem to show that the given equation has at least one solution in the indicated interval. Note that you are NOT asked to find the solution only show that at least one must exist in the indicated interval.

1. \(1 + 7{x^3} - {x^4} = 0\) on \(\left[ {4,8} \right]\)
2. \({z^2} + 11z = 3\) on \(\left[ { - 15, - 5} \right]\)
3. \(\displaystyle \frac{{{t^2} + t - 15}}{{t - 8}} = 0\) on \(\left[ { - 5,1} \right]\)
4. \(\ln \left( {2{t^2} + 1} \right) - \ln \left( {{t^2} + 4} \right) = 0\) on \(\left[ { - 1,2} \right]\)
5. \(10 = {w^3} + {w^2}{{\bf{e}}^{ - w}} - 5\) on \(\left[ {0,4} \right]\)

For problems 28 – 33 assume that \(f\left( x \right)\) is continuous everywhere unless otherwise indicated in some way. From the given information is it possible to determine if there is a root of \(f\left( x \right)\) in the given interval?

If it is possible to determine that there is a root in the given interval clearly explain how you know that a root must exist. If it is not possible to determine if there is a root in the interval sketch a graph of two functions each of which meets the given information and one will have a root in the given interval and the other will not have a root in the given interval.

1. \(f\left( { - 5} \right) = 12\) and \(f\left( 0 \right) = - 3\) on the interval \(\left[ { - 5,0} \right]\).
2. \(f\left( 1 \right) = 30\) and \(f\left( 9 \right) = 6\) on the interval \(\left[ {1,9} \right]\).
3. \(f\left( {20} \right) = - 100\) and \(f\left( {40} \right) = - 100\) on the interval \(\left[ {20,40} \right]\).
4. \(f\left( { - 4} \right) = - 10\), \(f\left( 5 \right) = 17\), \(\mathop {\lim }\limits_{x \to \,{1^ - }} f\left( x \right) = - 2\), and \(\mathop {\lim }\limits_{x \to \,{1^ + }} f\left( x \right) = 4\) on the interval \(\left[ { - 4,5} \right]\).
5. \(f\left( { - 8} \right) = 2\), \(f\left( 1 \right) = 23\), \(\mathop {\lim }\limits_{x \to \, - {4^ - }} f\left( x \right) = 35\), and \(\mathop {\lim }\limits_{x \to \, - {4^ + }} f\left( x \right) = 1\) on the interval \(\left[ { - 8,1} \right]\).
6. \(f\left( 0 \right) = - 1\), \(f\left( 9 \right) = 10\), \(\mathop {\lim }\limits_{x \to \,{2^ - }} f\left( x \right) = - 12\), and \(\mathop {\lim }\limits_{x \to \,{2^ + }} f\left( x \right) = - 3\) on the interval \(\left[ {0,9} \right]\).