Paul's Online Notes
Paul's Online Notes
Home / Calculus I / Derivatives / Interpretation of the Derivative
Show Mobile Notice Show All Notes Hide All Notes
Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Assignment Problems Notice
Please do not email me to get solutions and/or answers to these problems. I will not give them out under any circumstances nor will I respond to any requests to do so. The intent of these problems is for instructors to use them for assignments and having solutions/answers easily available defeats that purpose.

If you are looking for some problems with solutions you can find some by clicking on the "Practice Problems" link above.

Section 3.2 : Interpretation of the Derivative

For problems 1 – 3 use the graph of the function, \(f\left( x \right)\), estimate the value of \(f'\left( a \right)\) for the given values of \(a\).

    1. \(a = - 5\)
    2. \(a = 1\)
    This graph is a parabola that opens downward with vertex somewhere between x=-1 and x=0. To the left of the vertex the graph goes through the points (-5,-2) and (-2,4). To the right of the vertex the graph goes through the points (1,4) and (2, 3.75).
    1. \(a = - 2\)
    2. \(a = 3\)
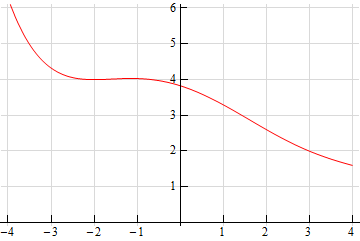
    This is a graph that starts at approximately (-4,6) and decreases until it hits (-2,4) where it goes through this point perfectly horizontal and then continues to decrease going through the points (1, 3.25) and (3,2).
    1. \(a = - 3\)
    2. \(a = 4\)
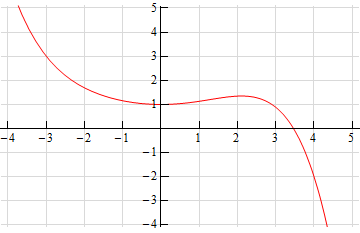
    This is a graph that starts at approximately (-3.8,5) and through the points (-3,3) and (0,1). It then increases until it reaches a peak somewhere between x=2 and x=3 and then decreases through the points (3,1) and (4,-2).

For problems 4 – 6 sketch the graph of a function that satisfies the given conditions.

  1. \(f\left( { - 7} \right) = 5\), \(f'\left( { - 7} \right) = - 3\), \(f\left( 4 \right) = - 1\), \(f'\left( 4 \right) = 1\)
  2. \(f\left( 1 \right) = 2\), \(f'\left( 1 \right) = 4\), \(f\left( 6 \right) = 2\), \(f'\left( 6 \right) = 3\)
  3. \(f\left( { - 1} \right) = - 9\), \(f'\left( { - 1} \right) = 0\), \(f\left( 2 \right) = - 1\), \(f'\left( 2 \right) = 3\), \(f\left( 5 \right) = 4\), \(f'\left( 5 \right) = - 1\)

For problems 7 – 9 the graph of a function, \(f\left( x \right)\), is given. Use this to sketch the graph of the derivative, \(f'\left( x \right)\).

  1. This is a graph that starts at approximately (-2, -0.8) and increases until it reaches a peak at x=-1 and approximately y=1.8. It then decreases until it reaches a valley at (3,9) and then increases until it ends at approximately (4, -6.8).
  2. This is a graph that starts at approximately (-2.8, 5) and increases until it reaches a peak at x=-2 and approximately y=4.2. It then decreases going through the origin perfectly flat and continuing to decrease until it reaches a valley at x=2 and approximately y=-4.2. It then increases until it ends at approximately (2.8, 5).
  3. This graph is a series of four line segments. The first line segment starts at (-6,3) and ends at (-3,-2). The second line segment starts at (-3,-2) and ends at (-1,5). The third line segment starts at (-1,5) and ends at (4,5). The final line segment starts at (4,5) and ends at (7,1).
  4. Answer the following questions about the function \(g\left( z \right) = 1 + 10z - 7{z^2}\).
    1. Is the function increasing or decreasing at \(z = 0\)?
    2. Is the function increasing or decreasing at \(z = 2\)?
    3. Does the function ever stop changing? If yes, at what value(s) of \(z\) does the function stop changing?
  5. What is the equation of the tangent line to \(f\left( x \right) = 5x - {x^3}\) at \(x = 1\).
  6. The position of an object at any time \(t\) is given by \(s\left( t \right) = 2{t^2} - 8t + 10\).
    1. Determine the velocity of the object at any time \(t\).
    2. Is the object moving to the right or left at \(t = 1\)?
    3. Is the object moving to the right or left at \(t = 4\)?
    4. Does the object ever stop moving? If so, at what time(s) does the object stop moving?
  7. Does the function \(R\left( w \right) = {w^2} - 8w + 20\) ever stop changing? If yes, at what value(s) of \(w\) does the function stop changing?
  8. Suppose that the volume of air in a balloon for \(0 \le t \le 6\)is given by\(V\left( t \right) = 6t - {t^2}\) .
    1. Is the volume of air increasing or decreasing at \(t = 2\)?
    2. Is the volume of air increasing or decreasing at \(t = 5\)?
    3. Does the volume of air ever stop changing? If yes, at what times(s) does the volume stop changing?
  9. What is the equation of the tangent line to \(f\left( x \right) = 5x + 7\) at \(x = - 4\)?
  10. Answer the following questions about the function \(Z\left( x \right) = 2{x^3} - {x^2} - x\).
    1. Is the function increasing or decreasing at \(x = - 1\)?
    2. Is the function increasing or decreasing at \(x = 2\)?
    3. Does the function ever stop changing? If yes, at what value(s) of \(x\) does the function stop changing?
  11. Determine if the function\(V\left( t \right) = \sqrt {14 + 3t} \) increasing or decreasing at the given points.
    1. \(t = 0\)
    2. \(t = 5\)
    3. \(t = 100\)
  12. Suppose that the volume of water in a tank for \(t \ge 0\) is given by \(\displaystyle Q\left( t \right) = \frac{{{t^2}}}{{t + 2}}\).
    1. Is the volume of water increasing or decreasing at \(t = 0\)?
    2. Is the volume of water increasing or decreasing at \(t = 3\)?
    3. Does the volume of water ever stop changing? If so, at what times(s) does the volume stop changing?
  13. What is the equation of the tangent line to \(g\left( x \right) = 10\) at \(x = 16\)?
  14. The position of an object at any time \(t\) is given by \(Q\left( t \right) = \sqrt {1 + 4t} \).
    1. Determine the velocity of the object at any time \(t\).
    2. Does the object ever stop moving? If so, at what time(s) does the object stop moving?
  15. Does the function \(Y\left( t \right) = 2{t^3} + 9t + 5\) ever stop changing? If yes, at what value(s) of \(t\) does the function stop changing?
[Contact Me] [Privacy Statement] [Site Help & FAQ] [Terms of Use]
© 2003 - 2024 Paul Dawkins
Page Last Modified : 11/16/2022