Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Assignment Problems Notice
Please do not email me to get solutions and/or answers to these problems. I will not give them out under any circumstances nor will I respond to any requests to do so. The intent of these problems is for instructors to use them for assignments and having solutions/answers easily available defeats that purpose.
If you are looking for some problems with solutions you can find some by clicking on the "Practice Problems" link above.
If you are looking for some problems with solutions you can find some by clicking on the "Practice Problems" link above.
Section 4.8 : Optimization
- Find two positive numbers whose sum of six times one of them and the second is 250 and whose product is a maximum.
- Find two positive numbers whose sum of twice the first and seven times the second is 600 and whose product is a maximum.
- Let \(x\) and \(y\) be two positive numbers whose sum is 175 and \(\left( {x + 3} \right)\left( {y + 4} \right)\) is a maximum. Determine \(x\) and \(y\).
- Find two positive numbers such that the sum of the one and the square of the other is 200 and whose product is a maximum.
- Find two positive numbers whose product is 400 and such that the sum of twice the first and three times the second is a minimum.
- Find two positive numbers whose product is 250 and such that the sum of the first and four times the second is a minimum.
- Let \(x\) and \(y\) be two positive numbers such that \(y\left( {x + 2} \right) = 100\) and whose sum is a minimum. Determine \(x\) and \(y\).
- Find a positive number such that the sum of the number and its reciprocal is a minimum.
- We are going to fence in a rectangular field and have 200 feet of material to construct the fence. Determine the dimensions of the field that will enclose the maximum area.
- We are going to fence in a rectangular field. Starting at the bottom of the field and moving around the field in a counter clockwise manner the cost of material for each side is $6/ft, $9/ft, $12/ft and $14/ft respectively. If we have $1000 to buy fencing material determine the dimensions of the field that will maximize the enclosed area.
- We are going to fence in a rectangular field that encloses 75 ft2. Determine the dimensions of the field that will require the least amount of fencing material to be used.
- We are going to fence in a rectangular field that encloses 200 m2. If the cost of the material for of one pair of parallel sides is $3/m and cost of the material for the other pair of parallel sides is $8/m determine the dimensions of the field that will minimize the cost to build the fence around the field.
- Show that a rectangle with a fixed area and minimum perimeter is a square.
- Show that a rectangle with a fixed perimeter and a maximum area is a square.
- We have 350 m2 of material to build a box whose base width is four times the base length. Determine the dimensions of the box that will maximize the enclosed volume.
- We have $1000 to buy the materials to build a box whose base length is seven times the base width and has no top. If the material for the sides cost $10/cm2 and the material for the bottom cost $15/cm2 determine the dimensions of the box that will maximize the enclosed volume.
- We want to build a box whose base length is twice the base width and the box will enclose 80 ft3. The cost of the material of the sides is $0.5/ft2 and the cost of the top/bottom is $3/ft2. Determine the dimensions of the box that will minimize the cost.
- We want to build a box whose base is a square, has no top and will enclose 100 m3. Determine the dimensions of the box that will minimize the amount of material needed to construct the box.
- We want to construct a cylindrical can with a bottom but no top that will have a volume of 65 in3. Determine the dimensions of the can that will minimize the amount of material needed to construct the can.
- We want to construct a cylindrical can whose volume is 105 mm3. The material for the wall of the can costs $3/mm2, the material for the bottom of the can costs $7/mm2 and the material for the top of the can costs $2/mm2. Determine the dimensions of the can that will minimize the cost of the materials needed to construct the can.
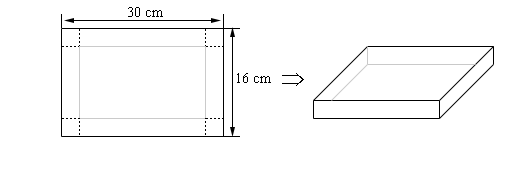
- We have a piece of cardboard that is 30 cm by 16 cm and we are going to cut out the corners and fold up the sides to form a box. Determine the height of the box that will give a maximum volume.
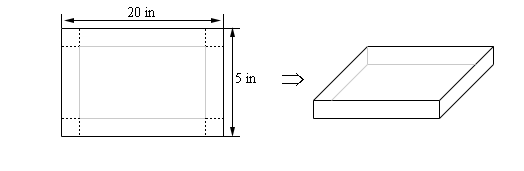
- We have a piece of cardboard that is 5 in by 20 in and we are going to cut out the corners and fold up the sides to form a box. Determine the height of the box that will give a maximum volume.
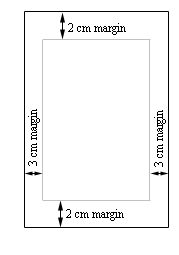
- A printer needs to make a poster that will have a total of 500 cm2 that will have 3 cm margins on the sides and 2 cm margins on the top and bottom. What dimensions of the poster will give the largest printed area?
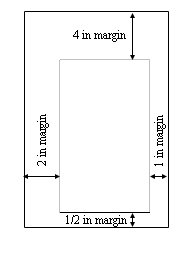
- A printer needs to make a poster that will have a total of 125 in2 that will have ½ inch margin on the bottom, 1 inch margin on the right, 2 inch margin on the left and 4 inch margin on the top. What dimensions of the poster will give the largest printed area?
