Calculus III - Double Integrals over General Regions (Assignment Problems)

Show Mobile Notice Show All Notes Hide All Notes

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Assignment Problems Notice

Please do not email me to get solutions and/or answers to these problems. I will not give them out under any circumstances nor will I respond to any requests to do so. The intent of these problems is for instructors to use them for assignments and having solutions/answers easily available defeats that purpose.

If you are looking for some problems with solutions you can find some by clicking on the "Practice Problems" link above.

Section 15.3 : Double Integrals over General Regions

Evaluate $ \displaystyle \iint\limits_{D}{{8y{x^3}\,dA}}$ where $D = \left\{ {\left( {x,y} \right)| - 1 \le y \le 2, - 1 \le x \le 1 + {y^2}} \right\}$
Evaluate $ \displaystyle \iint\limits_{D}{{12{x^2}y - {y^2}\,dA}}$ where $D = \left\{ {\left( {x,y} \right)| - 2 \le x \le 2, - {x^2} \le y \le {x^2}} \right\}$
Evaluate $ \displaystyle \iint\limits_{D}{{9 - \frac{{6{y^2}}}{{{x^2}}}\,dA}}$ where $D$ is the region in the 1^st quadrant bounded by $y = {x^3}$ and $y = 4x$.
Evaluate $ \displaystyle \iint\limits_{D}{{15{x^2} - 6y\,dA}}$ where $D$ is the region bounded by $x = \frac{1}{2}{y^2}$ and $x = 4\sqrt y $.
Evaluate $ \displaystyle \iint\limits_{D}{{6y{{\left( {x + 6} \right)}^2}\,dA}}$ where $D$ is the region bounded by $x = - {y^2}$ and $x = y - 6$.
Evaluate $ \displaystyle \iint\limits_{D}{{{{\bf{e}}^{{y^{\,2}} + 1}}\,dA}}$ where $D$ is the triangle with vertices $\left( {0,0} \right)$, $\left( { - 2,4} \right)$ and $\left( {8,4} \right)$.
Evaluate $ \displaystyle \iint\limits_{D}{{7{y^3}{{\bf{e}}^{{x^{\,2}} + 1}}\,dA}}$ where $D$ is the region bounded by$y = 2\,\,\sqrt[4]{x}$, $x = 9$ and the $x$-axis.
Evaluate $ \displaystyle \iint\limits_{D}{{{x^5}\sin \left( {{y^4}} \right)\,dA}}$ where $D$ is the region in the 2^nd quadrant bounded by $y = 3{x^2}$, $y = 12$ and the $y$-axis.
Evaluate $ \displaystyle \iint\limits_{D}{{xy - {y^2}\,dA}}$ where $D$ is the region shown below.
Evaluate $ \displaystyle \iint\limits_{D}{{12{x^3} - 3\,dA}}$ where $D$ is the region shown below.
$This region consists of two sub regions. The first sub region is the region in the fourth quadrant bounded by $y=x-1$, the x-axis and the y-axis. The second sub region is the region in the second quadrant bounded by $y=1-x^{2}$, the x-axis and the y-axis.$
Evaluate $ \displaystyle \iint\limits_{D}{{6{y^2} + 10y{x^4}\,dA}}$ where $D$ is the region shown below.
$This region consists of two sub regions. The first sub region is the region in the first and fourth quadrants bounded by $x=2-y^{2}$ and the y-axis. The second sub region is the region in the second and third quadrants bounded by $x=y^{2}-1$ and the y-axis.$
Evaluate $ \displaystyle \iint\limits_{D}{{\frac{{{x^3}}}{{{y^2}}}\,dA}}$ where $D$ is the region bounded by $\displaystyle y = \frac{1}{{{x^2}}}$, $x = 1$ and $\displaystyle y = \frac{1}{4}$ in the order given below.
1. Integrate with respect to $x$ first and then $y$.
2. Integrate with respect to $y$ first and then $x$.
Evaluate $ \displaystyle \iint\limits_{D}{{xy - {y^3}\,dA}}$ where $D$ is the region bounded by $y = {x^2}$, $y = - {x^2}$ and $x = 2$ in the order given below.
1. Integrate with respect to $x$ first and then $y$.
2. Integrate with respect to $y$ first and then $x$.

For problems 14 – 16 evaluate the given integral by first reversing the order of integration.

$\displaystyle \int_{0}^{8}{{\int_{{{y^{\frac{1}{3}}}}}^{2}{{\frac{y}{{{x^7} + 1}}\,dx}}\,dy}}$
$\displaystyle \int_{{ - 4}}^{0}{{\int_{{\sqrt { - x} }}^{2}{{{x^{ - \,\,\frac{2}{3}}}\,\,\sqrt {{y^{\frac{5}{3}}} + 1} \,dy}}\,dx}}$
$\displaystyle \int_{0}^{2}{{\int_{{ - x}}^{{3x}}{{5{y^2}{x^3} + 2\,dy}}\,dx}}$
Use a double integral to determine the area of the region bounded by $x = - {y^2}$ and $x = y - 6$.
Use a double integral to determine the area of the region bounded by $y = {x^2} + 1$ and $\displaystyle y = \frac{1}{2}{x^2} + 3$.
Use a double integral to determine the volume of the region that is between the $xy$‑plane and $f\left( {x,y} \right) = 2 - x{y^2}$ and is above the region in the $xy$-plane that is bounded by $y = {x^2}$ and $x = 1$.
Use a double integral to determine the volume of the region that is between the $xy$‑plane and $f\left( {x,y} \right) = 1 + {y^5}\,\,\sqrt {{x^4} + 1} $ and is above the region in the $xy$-plane that is bounded by $y = \sqrt x $, $x = 2$ and the $x$-axis.
Use a double integral to determine the volume of the region in the first octant that is below the plane given by $2x + 6y + 4z = 8$.
Use a double integral to determine the volume of the region bounded by $z = 3 - 2y$, the surface $y = 1 - {x^2}$ and the planes $y = 0$ and $z = 0$.
Use a double integral to determine the volume of the region bounded by the planes $z = 4 - 2x - 2y$, $y = 2x$, $y = 0$ and $z = 0$.
Use a double integral to determine the formula for the area of a right triangle with base, $b$ and height $h$.
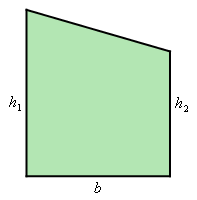
Use a double integral to determine a formula for the figure below.