Section 6.1 : Exponential Functions
3. Sketch each of the following.
- \(f\left( x \right) = {6^x}\)
- \(g\left( x \right) = {6^x} - 9\)
- \(g\left( x \right) = {6^{x + 1}}\)
Show All Solutions Hide All Solutions
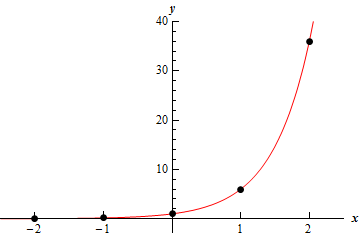
a Show SolutionWe can build up a quick table of values that we can plot for the graph of this function.
| \(x\) | \(f\left( x \right)\) |
|---|---|
| -2 | \(f\left( { - 2} \right) = {6^{ - 2}} = \frac{1}{{{6^{\,2}}}} = \frac{1}{{36}}\) |
| -1 | \(f\left( { - 1} \right) = {6^{ - 1}} = \frac{1}{6}\) |
| 0 | \(f\left( 0 \right) = {6^0} = 1\) |
| 1 | \(f\left( 1 \right) = {6^1} = 6\) |
| 2 | \(f\left( 2 \right) = {6^2} = 36\) |
Here is a quick sketch of the graph of the function.
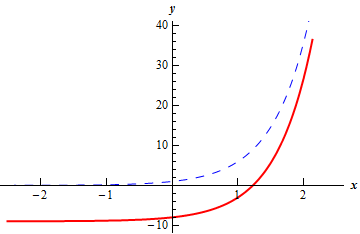
b Show Solution
For this part all we need to do is recall the Transformations section from a couple of chapters ago. Using the “base” function of \(f\left( x \right) = {6^x}\) the function for this part can be written as,
\[g\left( x \right) = {6^x} - 9 = f\left( x \right) - 9\]Therefore, the graph for this part is just the graph of \(f\left( x \right)\) shifted down by 9.
The graph of this function is shown below. The blue dashed line is the “base” function, \(f\left( x \right)\), and the red solid line is the graph for this part, \(g\left( x \right)\).
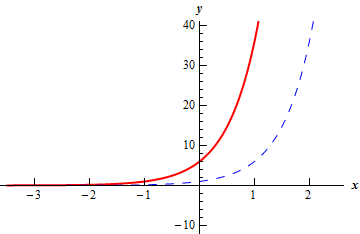
c Show Solution
For this part all we need to do is recall the Transformations section from a couple of chapters ago. Using the “base” function of \(f\left( x \right) = {6^x}\) the function for this part can be written as,
\[g\left( x \right) = {6^{x + 1}} = f\left( {x + 1} \right)\]Therefore, the graph for this part is just the graph of \(f\left( x \right)\) shifted left by 1.
The graph of this function is shown below. The blue dashed line is the “base” function, \(f\left( x \right)\), and the red solid line is the graph for this part, \(g\left( x \right)\).