Algebra - Lines

Show General Notice Show Mobile Notice Show All Notes Hide All Notes

General Notice

I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.

Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.

Paul
February 18, 2026

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 3.2 : Lines

Back to Problem List

2. Determine the slope of the line containing the two points below and sketch the graph of the line.

\[\left( {8,2} \right),\,\,\,\left( {14, - 7} \right)\]

Show All Steps Hide All Steps

Start Solution

Let’s find the slope of the line. We’ll let the first point listed above be the point \(\left( {{x_1},{y_1}} \right)\) and the second point listed be the point \(\left( {{x_2},{y_2}} \right)\) in the slope formula. Note that it doesn’t really matter which point is which. All that matters is that you stay consistent when you plug values into the formula.

Here’s the slope.

\[m = \frac{{ - 7 - 2}}{{14 - 8}} = \frac{{ - 9}}{6} = - \frac{3}{2}\] Show Step 2

Here is a sketch of the line.

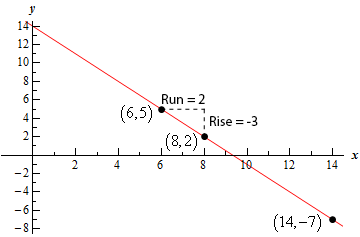
We’ve included an extra point, \(\left( {6,5} \right)\), to help illustrate the slope we computed in Step 1.