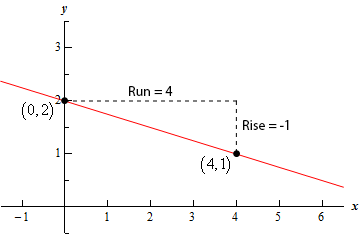Section 3.2 : Lines
6. Determine the slope of the line and sketch the graph of the following line.
\[4y + x = 8\]Show All Steps Hide All Steps
Start SolutionThe first thing that we should do here is write the equation of the line in slope-intercept form. This will help with both finding the slope and with sketching the graph.
Here is the slope-intercept form of the line.
\[4y = - x + 8\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}y = - \frac{1}{4}x + 2\] Show Step 2From the equation of the line in slope-intercept form that we found in the previous step we see that the slope is : \(\require{bbox} \bbox[2pt,border:1px solid black]{{ - \frac{1}{4}}}\) .
Show Step 3From the equation of line in slope-intercept form that we found in Step 1 we see that the \(y\)-intercept from of the line is \(\left( {0,2} \right)\) . Also, from the slope we found in Step 2 we know that the “rise” is -1 and the “run” is 4 and so a second point on the graph of the line is,
\[{x_2} = 0 + 4 = 4\hspace{0.25in}\hspace{0.25in}{y_2} = 2 + \left( { - 1} \right) = 1\hspace{0.25in} \Rightarrow \hspace{0.25in}\left( {4,1} \right)\]Using these two points we can sketch the graph of the line.