Section 4.2 : Parabolas
3. Sketch the graph of the following parabola. The graph should contain the vertex, the \(y\)‑intercept, \(x\)-intercepts (if any) and at least one point on either side of the vertex.
\[f\left( x \right) = 3{x^2} + 7\]Show All Steps Hide All Steps
Start SolutionLet’s find the vertex first. In this case we can consider the equation to be in the form \(f\left( x \right) = a{\left( {x - h} \right)^2} + k\) or we can use the form \(f\left( x \right) = a{x^2} + bx + c\). Either form will work and which you find to be the easiest will probably depend on you. We’ll use the first form so we can get another example of that form.
To make our equation up to the first form let’s do a little rewrite on our equation. Let’s write it as,
\[f\left( x \right) = 3{x^2} + 7 = 3{\left( {x - 0} \right)^2} + 7\]Note that we haven’t changed the equation! All we’ve done is use \(x = x - 0\) to get the forms to match up.
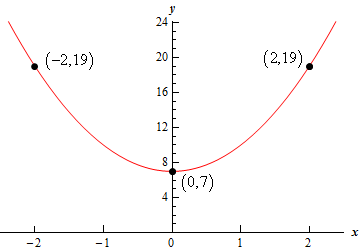
After doing this we can see that the vertex is : \(\left( {0,7} \right)\).
Also note that \(a = 3 > 0\) for this parabola and so the parabola will open upwards.
Show Step 2In this case we can see that the vertex above is on the \(y\)-axis (the \(x\) coordinate is zero!) and so it is also the \(y\)-intercept for the parabola!
Show Step 3For the \(x\)-intercepts we just need to solve the equation \(f\left( x \right) = 0\). So, let’s solve that for our equation.
\[\begin{align*}3{x^2} + 7 & = 0\\ 3{x^2} & = - 7\\ {x^2} & = - \frac{7}{3}\\ x & = \pm \sqrt { - \frac{7}{3}} = \pm \sqrt {\frac{7}{3}} \,i\end{align*}\]So, in this case the solutions to this equation are complex numbers and so we know that this parabola will have no \(x\)-intercepts.
Note that we did not really need to solve the equation above to see that there would be no \(x\)-intercepts for this problem. An alternate method would be to do the following analysis.
From the first step we found that the vertex was \(\left( {0,7} \right)\), which is above the \(x\)-axis, and we also noted that the parabola opened upwards. So, the parabola starts above the \(x\)-axis and opens upwards and we know that once a parabola starts opening in a given direction it won’t turn around and start going in the opposite direction. Therefore, because there is no way for the parabola to go down to the \(x\)-axis, there is no way for there to be \(x\)‑intercepts for this problem.
Show Step 4In this case we didn’t have \(x\)-intercepts and the \(y\)-intercept also happens to be the vertex. So, at this point we have only have one point on the graph. To get points on either side of the vertex all we need to do is do a couple of quick function evaluations to find points on either side of the vertex.
We’ll use the following two points.
\[\left( { - 2,f\left( { - 2} \right)} \right) = \left( { - 2,19} \right)\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\left( {2,f\left( 2 \right)} \right) = \left( {2,19} \right)\] Show Step 5Here is a sketch of the parabola including all the points we found above.