Section 6.2 : Area Between Curves
6. Determine the area of the region bounded by \(x = {y^2} - y - 6\) and \(x = 2y + 4\).
Show All Steps Hide All Steps
Let’s start off with getting a sketch of the region we want to find the area of.
We are assuming that, at this point, you are capable of graphing most of the basic functions that we’re dealing with in these problems and so we won’t be showing any of the graphing work here.
Here is a sketch of the bounded region we want to find the area of.
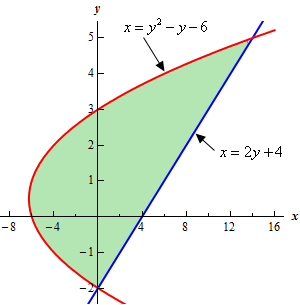
Note that we won’t include any portion of the region above the top intersection point or below the bottom intersection point. The region needs to be bounded by one of the given curves on each boundary. If we went past the top intersection point we would not have an upper bound on the region. Likewise, if we went past the bottom intersection point we would not have a lower bound on the region.
Show Step 2It should be clear from the graph that the right function is \(x = 2y + 4\) and the left function is \(x = {y^2} - y - 6\).
Since we weren’t given any limits on \(y\) in the problem statement we’ll need to get those. However, we should never just assume that our graph is accurate or that we will be able to read it accurately enough to guess the coordinates from the graph. This is especially true when the intersection points of the two curves (i.e. the limits on \(y\) that we need) do not occur on an axis (as they don’t in this case).
So, to determine the intersection points correctly we’ll need to find them directly. The intersection points are where the two curves intersect and so all we need to do is set the two equations equal and solve. Doing this gives,
\[{y^2} - y - 6 = 2y + 4\hspace{0.25in} \to \hspace{0.25in}{y^2} - 3y - 10 = \left( {y - 5} \right)\left( {y + 2} \right) = 0\hspace{0.25in} \to \hspace{0.25in}y = - 2,\,\,\,\,y = 5\]Therefore the limits on \(y\) are : \[ - 2 \le y \le 5\].
Note that you may well have found the intersection points in the first step to help with the graph if you were graphing by hand which is not a bad idea with faced with graphing this kind of region.
Show Step 3At this point there isn’t much to do other than step up the integral and evaluate it.
We are assuming that you are comfortable with basic integration techniques so we’ll not be including any discussion of the actual integration process here and we will be skipping some of the intermediate steps.
The area is,
\[A = \int_{{ - 2}}^{5}{{2y + 4 - \left( {{y^2} - y - 6} \right)\,dy}} = \int_{{ - 2}}^{5}{{10 + 3y - {y^2}\,dy}} = \left. {\left( {10y + \frac{3}{2}{y^2} - \frac{1}{3}{y^3}} \right)} \right|_{ - 2}^5 = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{343}}{6}}}\]