Section 1.1 : Review : Functions
27. Find the domain of \(h\left( x \right) = \sqrt {{x^4} - {x^3} - 20{x^2}} \).
Show All Steps Hide All Steps
In this case we need to avoid square roots of negative numbers so we need to require,
\[{x^4} - {x^3} - 20{x^2} = {x^2}\left( {{x^2} - x - 20} \right) = {x^2}\left( {x - 5} \right)\left( {x + 4} \right) \ge 0\]Once we have the polynomial in factored form we can see that the left side will be zero at \(x = 0\), \(x = - 4\) and \(x = 5\). Because the quantity under the radical is a polynomial we know that it can only change sign if it goes through zero and so these are the only points the only places where the polynomial on the left can change sign.
Here is a number line giving the value/sign of the polynomial at a test point in each of the region defined by these three points. To make it a little easier to read the number line let’s define the polynomial under the radical to be,
\[R\left( x \right) = {x^4} - {x^3} - 20{x^2} = {x^2}\left( {x - 5} \right)\left( {x + 4} \right)\]Now, here is the number line,
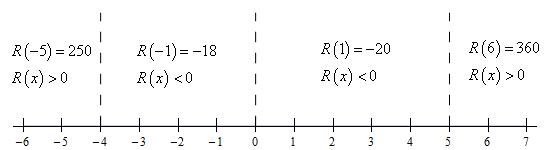
The domain will then be all the points where the polynomial under the root is positive or zero and so the domain is,
\[{\rm{Domain : }} - \infty < x \le - 4,\,\,\,x = 0,\,\,\,5 \le x < \infty \]In this case we need to be very careful and not miss \(x = 0\). This is the point separating two regions which give negative values of the polynomial, but it will give zero and so it also part of the domain. This point is often very is very easy to miss.