Calculus I - Linear Approximations

Show All Notes Hide All Notes

2. Find a linear approximation to \(h\left( t \right) = {t^4} - 6{t^3} + 3t - 7\) at \(t = - 3\).

Show All Steps Hide All Steps

Start Solution

We’ll need the derivative first as well as a couple of function evaluations.

\[h'\left( t \right) = 4{t^3} - 18{t^2} + 3\hspace{0.5in}h\left( { - 3} \right) = 227\hspace{0.5in}h'\left( { - 3} \right) = - 267\] Show Step 2

There really isn’t much to do at this point other than write down the linear approximation.

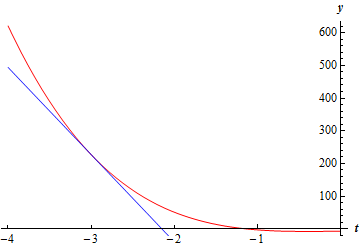
\[\require{bbox} \bbox[2pt,border:1px solid black]{{L\left( t \right) = 227 - 267\left( {t + 3} \right) = - 267t - 574}}\]

While it wasn’t asked for, here is a quick sketch of the function and the linear approximation.