Section 4.9 : More Optimization
5. A line through the point \(\left( {2,5} \right)\) forms a right triangle with the \(x\)-axis and \(y\)-axis in the 1st quadrant. Determine the equation of the line that will minimize the area of this triangle.

Show All Steps Hide All Steps
Start SolutionThis problem may seem a little tricky at first. Here is a sketch of a line that goes through the point \(\left( {2,5} \right)\), has an \(x\)-intercept of \(\left( {a,0} \right)\) and a \(y\)-intercept of \(\left( {0,b} \right)\).
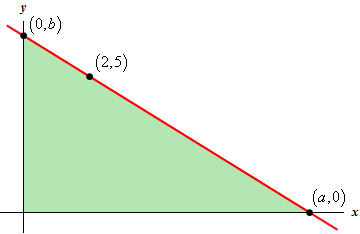
Note that the only way we can get a triangle with the line, \(x\)-axis and \(y\)-axis as sides is to require that \(a > 2\) and \(b > 5\). If either of those are not true we will not have the triangle that we want.
Show Step 2Next, we need to set up the constraint and equation that we are being asked to optimize.
We are being asked to minimize the area of the triangle shown above. In terms of the quantities given on the graph it is easy enough to get an equation for the area. The base length of the triangle is \(a\) and the height of the triangle is \(b\). We don’t have values for either of these but that isn’t a problem. Here is the area of the triangle.
\[A = {\frac{1}{2}}ab\]The constraint in this case is the equation of the line since that will define the hypotenuse of the triangle and hence also give both the base and height of the triangle. We need to write down the equation of the line, but we have three points on the line that we can use. Note however, that we really should use \(\left( {2,5} \right)\) as one of the points because the line does need to go the point and using this point to write down the equation will give us that without any extra work.
The real question then is whether we should use the \(x\) or \(y\)-intercept for the second point when determining the slope of the line. It really doesn’t matter which point that you use. The work will be slightly different for each point but there will be no real difference in the difficulty of the problem.
We are going to use \(\left( {a,0} \right)\) for the second point. The slope of the line using this point is,
\[m = \frac{5}{{2 - a}}\]We already know that \(b\) is the \(y\)-intercept and so the equation of the line through the point is,
\[y = \frac{5}{{2 - a}}x + b\]Note that we definitely seem to have a problem here. Normally at this point we’ve got two equation and two unknowns. In this case we appear to have four unknowns : \(a\), \(b\), \(x\) and \(y\). This isn’t a problem as well see in the next step.
Show Step 3We now need to solve the constraint for one of the unknowns in the area function, \(i\).e either \(a\) or \(b\). However, as we noted above we also have an \(x\) and \(y\) in the equation that will cause problems if they stay in the equation.
The point of this step is to get the area function down to a single variable. If we leave the \(x\) and \(y\) in the equation of the line we will end up with an area function with not one variable but three and that won’t work for us.
What we really need is an equation involving only \(a\) and \(b\) that we can solve for one or the other and plug into the area function. Luckily this is easy to get. All we need to do is plug the \(x\)-intercept into the equation of the line to get,
\[0 = \frac{5}{{2 - a}}a + b\]Do you see why we couldn’t have used the \(y\)-intercept here? If not, plug it in and you’ll very quickly see why it won’t work.
At this point we can easily solve the equation for \(b\) to get,
\[b = - \frac{{5a}}{{2 - a}} = \frac{{5a}}{{a - 2}}\]To eliminate one of the minus signs we took the minus sign in front of the quotient and applied it to the denominator and simplified. This doesn’t need to be done, but it does eliminate one of them.
Note that if we had used the \(y\)-intercept to determine the slope we would have found it to be easier at this step to solve for \(a\) instead. That is the only real difference in which point you use to find the slope.
Okay, let’s put all this together. We know the value of \(b\) in terms of \(a\) so plug that into the area function to get,
\[A\left( a \right) = \frac{1}{2}\left( a \right)\left( {\frac{{5a}}{{a - 2}}} \right) = \frac{5}{2}\frac{{{a^2}}}{{a - 2}}\] Show Step 4Here is the derivative of the area function,
\[A'\left( a \right) = \frac{5}{2}\frac{{{a^2} - 4a}}{{{{\left( {a - 2} \right)}^2}}} = \frac{5}{2}\frac{{a\left( {a - 4} \right)}}{{{{\left( {a - 2} \right)}^2}}}\]From this it looks like we get a three potential critical points : \(a = 0\), \(a = 2\) and \(a = 4\).
We can’t use \(a = 0\) as the critical point because that will no longer form a triangle with both the \(x\)-axis and the \(y\)-axis as the problem asks for as noted in the first step.
We also can’t use \(a = 2\) for two reasons. First, it isn’t actually a critical point because the area function doesn’t exist at \(a = 2\). This shouldn’t be surprising given that if we used this point we wouldn’t have a triangle anyway (again as we noted in the first step) and that is also the second reason for not using it.
This leaves only \(a = 4\) as a potential critical point that we can use.
Show Step 5The second derivative of the area function (after a little simplification) is,
\[A''\left( a \right) = \frac{{20}}{{{{\left( {a - 2} \right)}^3}}}\]From this we can see that the second derivative is always positive provided we have \(a > 2\). However, as we noted in the first step this is required in order even work the problem. Therefore, the second derivative will always be positive for the range of \(a\) that we are working on. The area function will then will always be concave up for the range of \(a\) and \(a = 4\) must give a minimum area.
Show Step 6Now that we know the value of \(a\) we know that the slope and \(y\)-intercept are,
\[m = \frac{5}{{2 - 4}} = - \frac{5}{2}\hspace{0.5in}\hspace{0.5in}b = \frac{{5\left( 4 \right)}}{{4 - 2}} = 10\]The equation of the line is then,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{y = - \frac{5}{2}x + 10}}\]