Section 4.9 : More Optimization
7. Two 10 meter tall poles are 30 meters apart. A length of wire is attached to the top of each pole and it is staked to the ground somewhere between the two poles. Where should the wire be staked so that the minimum amount of wire is used?
Show All Steps Hide All Steps
Start SolutionLet’s start with a quick of the situation with some more information added in.
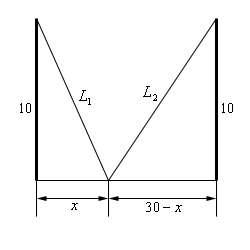
Next, we need to set up the constraint and equation that we are being asked to optimize.
We want to minimize the amount of wire and so the equation we need to minimize is,
\[L = {L_1} + {L_2}\]The constraint here is that the poles must be 30 meters apart. We can use this to determine the lengths of the individual wires in terms of \(x\). Doing this gives,
\[{L_1} = \sqrt {100 + {x^2}} \hspace{0.5in}{L_2} = \sqrt {100 + {{\left( {30 - x} \right)}^2}} \]Note that as well can also see that we need to require that \(0 \le x \le 30\).
Show Step 3All we need to do here is plug the lengths of the individual wires in the total length to get a function in terms of \(x\) that we can minimize.
\[L\left( x \right) = \sqrt {100 + {x^2}} + \sqrt {100 + {{\left( {30 - x} \right)}^2}} \] Show Step 4The derivative of the length function is,
\[L'\left( x \right) = \frac{x}{{\sqrt {100 + {x^2}} }} + \frac{{x - 30}}{{\sqrt {{x^2} - 60x + 1000} }}\]Solving for the critical point(s) is going to be messy so here it goes.
\[\begin{align*}\frac{x}{{\sqrt {100 + {x^2}} }} + \frac{{x - 30}}{{\sqrt {{x^2} - 60x + 1000} }} & = 0\\ \frac{x}{{\sqrt {100 + {x^2}} }} & = - \frac{{x - 30}}{{\sqrt {{x^2} - 60x + 1000} }}\\ x\sqrt {{x^2} - 60x + 1000} & = - \left( {x - 30} \right)\sqrt {100 + {x^2}} \\ {x^2}\left( {{x^2} - 60x + 1000} \right) & = {\left( {x - 30} \right)^2}\left( {100 + {x^2}} \right)\\ {x^4} - 60{x^3} + 1000{x^2} & = {x^4} - 60{x^3} + 1000{x^2} - 6000x + 90000\\ 0 & = - 6000x + 90000\\ x & = 15\end{align*}\]A quick check by plugging this back into the derivative shows that we do indeed get \(L'\left( 15 \right) = 0\) and so this is a critical point and it is in the acceptable range of \(x\).
Recall that because we squared both sides of the equation above it is possible to end up with answers that in fact are not solutions and so we have to go back and check in the original equation to make sure that they are solutions.
Show Step 5Since we have a range of \(x\)’s and the distance function is continuous in the range all we need to do is plug in the endpoints and the critical point to identify the minimum distance.
\[L\left( 0 \right) = 41.6228\hspace{0.5in}L\left( 15 \right) = 36.0555\hspace{0.5in}L\left( {30} \right) = 41.6228\] Show Step 6The wire should be staked midway between the poles to minimize the amount of wire.